一般指派問題的LINGO解法討論

錢麗麗

(無錫機電高等職業技術學校，江蘇 無錫 214000)

引言

在日常生活安排和企業生產管理工作中，經常會遇到給人分派工作或給機器指派任務等一般指派問題。一般指派問題是最優化問題的一種，它的問題模型是給n個人(本文中的人泛指可以執行任務的一切物體)指派完成m項任務，根據每個人完成每項任務的工作效率來研究如何分配任務，使完成任務所消耗的總資源最少或總收益最大。指派問題是0-1型整數規劃問題中比較常見的一種，它的特點是決策變量只有0和1兩種取值，在問題討論時，通常把某個人是否執行某項任務取值為1和0，建立一般指派問題與0-1規劃對應關系。當指派人數和任務數都比較大或數量關系不對等時，問題的模型就會變得復雜，求解也更加困難。因此，本文引入了LINGO這款軟件，LINGO是美國LINDO系統公司專門開發用于求解優化模型的數學軟件，主要用于求解線性、非線性和整數優化模型，它內置了一種建立最優化模型的語言，可以簡便地表達大規模問題，利用LINGO高效的求解器可以快速求解并分析結果[1]。本文通過對一般指派問題建立0-1規劃模型，分析模型，并借助LINGO求解法實現對此類問題的討論。

目前，一般指派問題根據人數和任務數的數量關系大致有以下三種情況：(1)人數和任務數相等，即每個人必須只完成一項任務；(2)人數小于任務數，一個人可以完成幾項任務；(3)人數大于任務數，一項任務可由幾個人來完成。其中，第一種指派為標準指派，它是一種最基礎的指派，人與任務一一對應；第二、第三種指派屬于非標準指派。本文通過具體的案例，給出這三種情況的LINGO解法[2]。

一、標準指派問題

例1：有4個工人，要指派他們完成4項任務， 規定每人只能做1項任務, 每項任務只能1個人做，每人做各項任務所消耗的時間如表1所示，如何分派任務，可使總的消耗時間最少[3]？

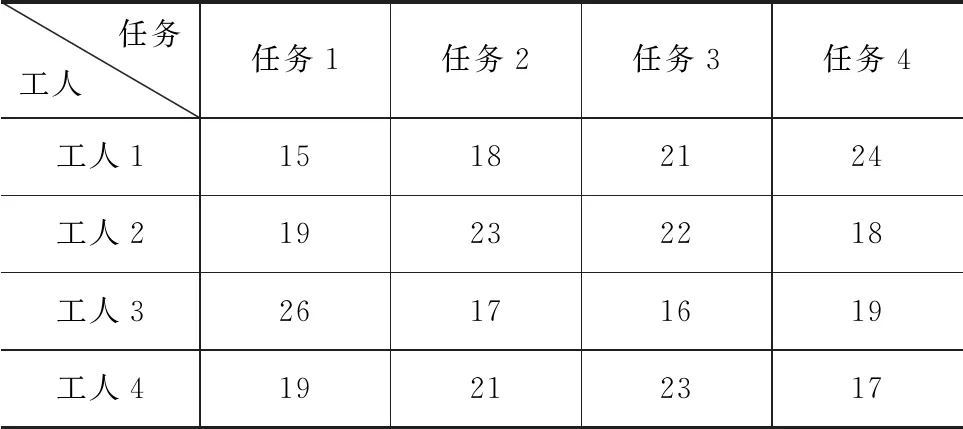
表1 任務分配問題

問題分析：這是典型的指派問題，每個工人必須做且只能做1項工作，第i個工人是否做第j個工作可以用0-1型變量表示。所以這類問題的數學模型是0-1型整數規劃。

(一)模型建立

1.決策變量

2.目標函數

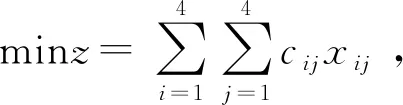
3.約束條件

set:

Worker/1..4/;

Job /1..4/;

Assign(work,job):c,x;

endsets

data:

enddata

min=@sum(Assign:c*x);

@for(worker(i):@sum(job(j):x(i,j))=1);

@for(job(j):@sum(worker(i):x(i,j))=1);

@for(Assign:@bin(x));

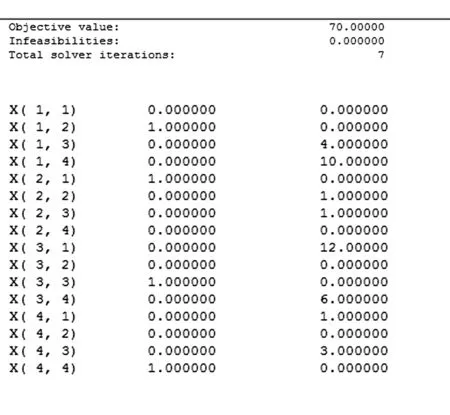
(二)模型結果分析

運行結果中的x(i，j)=1表示第i個工人執行第j項任務，x(i，j)=0則表示不執行，故當工人1→任務2，工人2→任務1，工人3→任務3，工人4→任務4，所用的總時間最省，共70小時。

用LINGO求解標準指派問題程序語言比較簡單，它的語句順序可以交換，字母可以不區分大小寫，但必須是輸入能被軟件識別的符號或語言，否則哪怕是一個微小的錯誤也會導致程序無法運行，所以在編程時除了要按照正常的要求編寫外，還應注意一些細節：如變量名只能由字母和數字組成，變量不能出現在約束條件的右端，調用函數必須以符號@開頭，函數后面的變量必須加括號等[4]。

二、非標準指派問題

例2：某公司計劃開5家新店，并決定由該公司下面的3家建筑公司來負責完成。3家建筑公司Ai(i=1,2,3)對5家新店Bj(j=1,2,3,4,5)的建筑費Cij(i=1,2,3,j=1,2,3,4,5)如表2所示，且允許每家建筑公司承建1家或2家商店，但每家商店只能由1家公司承擔，問如何對5家新店分配建造任務，可以使建造費用最小。

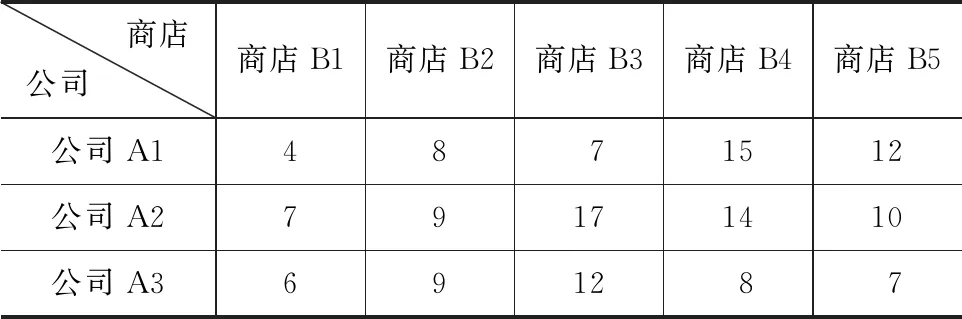
表2 公司承建商店問題 單位：萬元

(一)問題分析

由于公司少商店多，且每家公司最多可以承擔2家新店，因此，可以把每家公司化作相同的2家公司，然后再添加虛擬的一列B6，各公司承建商店B6的費用均為0，用系數矩陣來表示出這種變化：

B1B2B3B4B5 B1B2B3B4B5B6

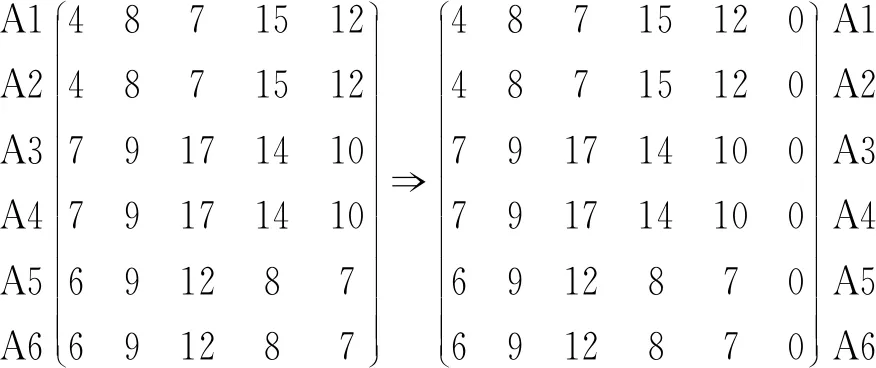
用LINGO軟件求解

sets:

company/1..6/;

shop /1..6/;

Assign(company,shop):c,x;

endsets

data:

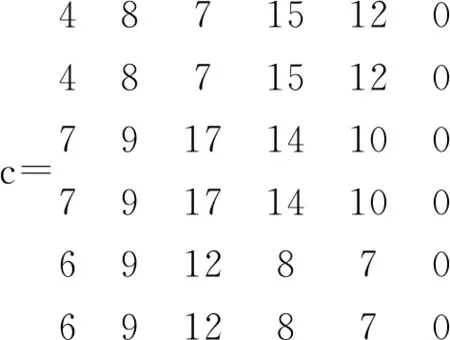
enddata

min=@sum(Assign:c*x);

@for(shop(j):@sum(company(i):x(i,j))=1);

@ for(company(i):@sum(shop(j):x(i,j))=1);

@for(Assign:@bin(x));

運行結果顯示出有效數據：x(1,1)，x(2,3)，x(3,6)，x(4,2)，x(5,5)，x(6,4)為可行方案，且最小值為35。為了問題研究的方便，把原來的3家公司假設成了相同的6家，因此，i取1和2、3和4、5和6分別表示公司A1，公司A2，公司 A3，j取1—5表示商店1—商店5，j取6表示沒有商店。故當公司A1承建商店B1和B3，公司A2承建商店B2，公司A3承建商店B4和B5時，所消耗的總建筑費用最省，共需35萬元。

例3：有6個人甲、乙、丙、丁、戊、戌要翻譯日文、韓文、英文和俄文4本書，他們每個人都精通這4種語言，各自翻譯1本書所需的時間如表3所示，每個人只能翻譯1本書，1本書可以由1個人或2個人來翻譯，問如何分配任務，可以使他們總共花的時間最少？

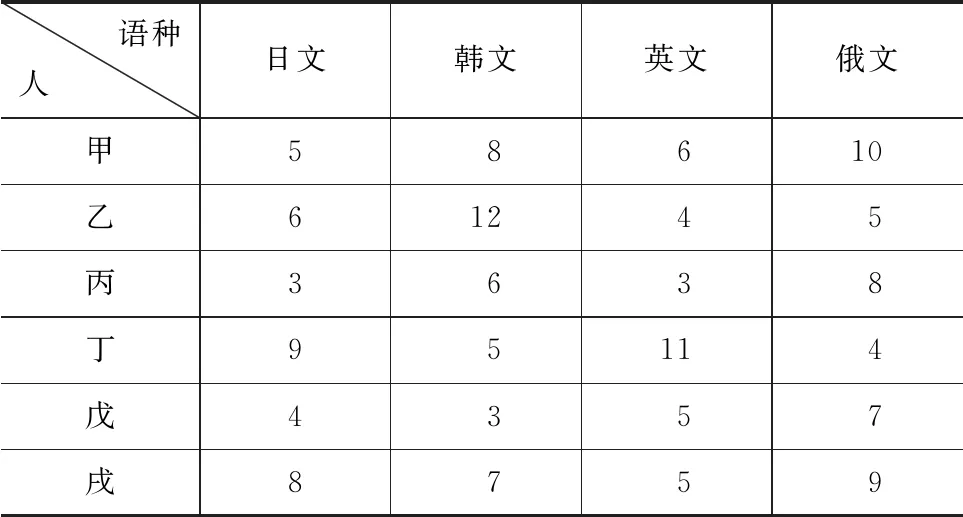
表3 翻譯問題

問題分析：1本語言書可以由2個人翻譯，可以把每1本書變成2本相同的書，問題可看成6個人翻譯8本語言書，缺少的2個人數用虛擬的2個人補足，虛擬的2個人翻譯每本書所用的時間為0，用系數矩陣表示出這種變化：

(二)編寫LINGO程序

sets:

person /1..8/;

language /1..8/;

Assign(person,language):c,x;

endsets

data:

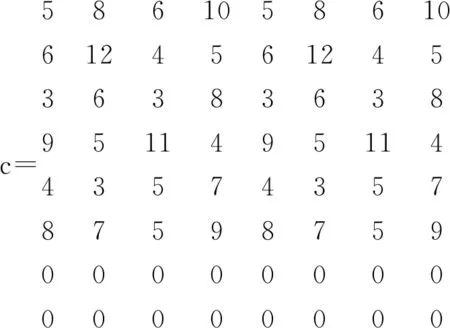
enddata

min=@sum(Assign:c*x);

@for(language(j):@sum(person(i):x(i,j))

=1);

@for(person(i):@sum(language(j):x(i,j))=1);

@for(Assign:@bin(x));

運行程序結果顯示，甲和丙翻譯日文書，乙和戌翻譯英文書，丁翻譯俄文書，戊翻譯韓文書，6個人翻譯8本書的總共時間最少為24小時，由于8本書是原來4本書的疊加，所以6個人翻譯8本書所花的時間應該是6個人翻譯4本書的兩倍，故實際最少時間應該是12小時。

在解決以上兩種非標準指派問題時可以通過增加虛擬的“人”或虛擬的“事”來轉化為標準指派問題。其中，增設的虛擬人做各種事的費用或產生的效益均為0，同樣，增加的虛擬的事被人完成所需的費用或能產生的效益也是0。當然，還要注意的是，幾個人完成同一件事的時間并不是他們獨立完成這件事時間的簡單疊加，所以應根據實際情況對計算結果進行一定分析和處理。

結束語

一般指派問題是生產管理者在日常工作中經常會遇到的一類問題。用LINGO軟件求解標準指派問題能更高效地表達目標函數與約束條件，所編的程序語言幾乎是對數學模型的翻譯，不需要太多的轉換,程序結果簡潔易懂，即使初學者也能快速掌握。而本文中討論的兩種非標準指派問題最終都能通過一定的條件假設轉化為標準指派問題來求解。當然，還有一些其他的非標準指派，如限定某人一定不能做某項工作或者必須做某項工作的情況更為復雜，不屬于一般的范疇，這里就不作深入討論了。