面向健康醫療的分類關聯規則挖掘研究

孫明瑞, 臧天儀

(哈爾濱工業大學 計算機科學與技術學院, 哈爾濱 150001)

0 引 言

數據挖掘技術是從海量數據集中挖掘出用戶感興趣的物品或知識，這些知識是隱式的、未知的，挖掘出的知識表示為定律、規律、規則等形式。關聯分析(Association Analysis)是數據挖掘的基礎，用以挖掘大規模、海量數據中隱式的規則關系模式。大規模數據間存在關聯關系，變量的取值也存在某種規律性，但數據間的關系是復雜的、隱式存在的，關聯分析的目的就是挖掘數據間的隱藏關聯信息，對健康醫療領域具有新的價值。典型的規則如購物籃事務(Market Basket Transaction),“如果用戶購買了嬰兒尿布，那么該用戶購買啤酒的概率為33%”，產生的關系可以用關聯規則(Association Rule)或頻繁模式(Frequent Pattern)表示，用以反映用戶偏好的有用規則。

基于以上的分析和討論，本文提出了針對個人健康信息數據的頻繁特征項挖掘算法，擴展了關聯規則頻繁模式的概念，引入連續性特征屬性值并給出離散化的解決方案，改進了關聯規則的一般模式，提出了分類關聯規則挖掘算法，對健康醫療領域和其它領域中基于關聯規則的推薦具有重要的指導意義和研究價值。

1 相關工作

關聯規則挖掘是數據挖掘的一個重要研究方向，描述了交易數據集中2組不同對象之間存在的某種關聯關系。在關聯規則挖掘過程中，需要對交易數據集進行多次掃描并與候選頻繁項目集進行匹配和計數。由于面對巨量交易數據集，這一匹配和計算過程需要花費大量時間，因此效率是設計算法的關鍵。

1994年Agrawal等人[1]開創性地提出了Apriori算法，用來發現購物籃中有趣的關聯關系，基于“所有長頻繁項目集的子集都是頻繁”的思想，對候選頻繁項目集進行剪枝，使候選頻繁項目集更小，從而顯著改進頻繁項目集算法的性能。自此，學界進行了廣泛的研究，來解決關聯分析中的實現和應用等問題。FP-growth[2]算法實現了FP-tree的構造及在FP-tree上進行挖掘，在效率上較之Apriori算法有很大的提高。Park等人[3]在1995年提出一種高效地產生頻繁項目集的基于雜湊的DHP算法。Savasere等人[4]設計了基于劃分的算法。Toivonen[5]提出了一種基于采樣的算法，其核心是隨機從數據集中采集樣本S，然后搜索S中的頻繁項集。惠曉濱等人[6]提出了基于頻繁模式棧變換的高效關聯規則算法。以上這些算法都是從算法實現問題的角度來解決頻繁項集挖掘。

分類關聯規則(Class Association Rules)是對關聯規則的擴展，用以區分或判別實例類標簽的關聯規則。1998年，Liu等人[7]率先提出了分類關聯規則算法CBA。Wang等人[8]融合分類關聯規則和決策樹的優勢，提出關聯決策樹ADT算法。Xu等人[9]首次提出利用原子型分類關聯規則構建分類器的思想，創立了原子關聯規則分類(CAAR)新技術。

綜上所述，與傳統的關聯規則相比，分類關聯規則具有更高的準確性及魯棒性。作為一種新的特征匹配方法，如何處理連續屬性特征，如何以較小的代價挖掘頻繁項集，如何從大量關聯規則中提取有效的分類關聯規則，是本文研究的重點內容。

2 問題的定義

針對關聯規則模式的挖掘，本次研究的目標是將數據的最后一列特征屬性類別標識設置為關聯規則的后件，即挖掘分類關聯規則，而非全局關聯規則。設I={i1,i2, …,in}為具有n個特征屬性的數據集合(項集約束)，y表示類別標識屬性，且y∩I=?。分類關聯規則的挖掘目標是形如X→y的分類關聯關系，其中X∈I。

3 算法研發與設計

3.1 先驗性原理

一般地，包含k個項的數據集會產生2k-1個頻繁項集，由于k的值可能非常大，導致項集搜索空間的時間復雜度是指數級規模的O(2n)。因此引入如下定理：

定理 先驗(Apriori)原理如果一個項集是頻繁的，則其所有的子集也一定是頻繁的。

引理如果項集是非頻繁的，則其所有超集也都是非頻繁的。

性質 單調性原理設I是項的集合，J=2I是I的冪集。度量f是單調的(向上封閉的)，當

?X,Y∈J:(X?Y)→f(X)≤f(Y),

(1)

其中，X為Y的子集，則f(X)一定不會超過f(Y)。

另一方面，f是反單調的(向下封閉)，當

?X,Y∈J:(X?Y)→f(Y)≤f(X).

(2)

根據性質，如圖1所示，通常可以采用自頂向下(從1維到n維的項集搜索)或自底向上(從n維到1維的項集搜索)的搜索策略挖掘頻繁項集。

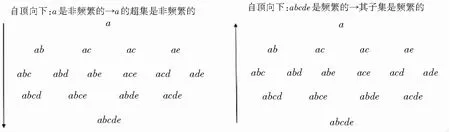
圖1 頻繁項集封閉性原則

3.2 頻繁項集挖掘算法

Apriori算法基于支持度剪枝技術，采用分層的完備搜索算法(深度優先)，依據性質向下封閉性，對關聯規則進行挖掘，能有效防止項集的指數級增長。算法的功能是挖掘支持度大于等于minsup的項集。算法首先生成單個元素項集列表，通過掃描數據集計算滿足最小支持度的項集，刪除不滿足最小支持度的項集。對單個元素的項集進行組合以生成2個元素的項集。然后，重新掃描數據集，刪除不滿足最小支持度的項集，重復該過程直到所有項集都被刪除。頻繁項集挖掘算法的設計描述見如下。

算法1 頻繁項集挖掘算法

輸入數據集I，最小支持度minsup，頻繁項集個數kmax

輸出頻繁項集Fk

k←random integer from 1 tokmax

Ifk=1 thenFk←{i|i∈I∧σ(i)≥N×minsup} //發現所有的頻繁1-項集

Else do

k←k+1

Ck←apriori-gen(Fk-1)//產生候選項集

For eacht∈Tdo

Ct←subset(Ck,t)

//識別屬于t的所有候選

For eachc∈Ctdo

σ(c)←σ(c)+1

//支持度計數增值

End for

End for

Fk←{c|c∈Ck∧σ(c)≥N×minsup} //提取頻繁k-項集

UntilFk=?

Return ∪Fk

3.3 候選項集的挖掘和剪枝

候選項集挖掘通過合并頻繁k-1項集，當且僅當前k-2項都相同。這里設X={x1,x2,…,xk-1}和Y={y1,y2,…,yk-1}是頻繁k-1項集，合并X和Y，當其均滿足如下公式：

xi=yi(i=1, 2,…,k-2)且xi-1≠yi-1.

(3)

3.4 算法的時間復雜度

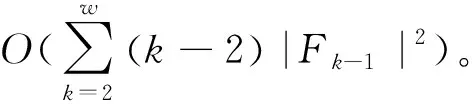
3.5 分類關聯規則挖掘算法

針對分類關聯規則挖掘，關聯規則的后件為類別標識，即形如X→y的分類關聯規則。通過3.2節頻繁項集挖掘，研究得到了最大頻繁項集Fk，由其產生的子集可作為分類關聯規則的前件，而目標類標識作為關聯規則后件，是一種存在具體搜索目標的挖掘優化問題，同時需要滿足設定的最小支持度和最小置信度閾值要求。這里，給出了分類關聯規則挖掘算法的研發代碼詳見如下。

算法2 分類關聯規則挖掘算法

輸入頻繁k項集Fk

輸出分類關聯規則Car

For (i=2;Fi-1≠?;i++) Do

Ck←Car-candidate-gen(Fi-1);

Foreachfrequentitemsetf∈FkDo

Foreachcandidatec∈CkDo

Ifc.classsetiscontainedinfThen

c.classsupCount++;

Iff.class=c.classThen

c.rulesupCount++;

End for

End for

Cark←{f|f∈Fk,f.rulesupCount/f.classsupCount≥minconf};

End for

Return ∪Cark

4 實驗評估

實驗采用公開的臨床數據集：加州大學歐文分校慢性腎病(Chronic Kidney Disease，CKD)數據集和皮膚病(Dermatology)數據集。考慮到數據集具有一定程度的缺失度，因此采用均值插值的方法對缺失值進行插值，并對連續屬性項進行離散化分類處理。挖掘個人健康數據之間隱式關系、頻繁項集、及分類關聯規則模式。

慢性腎病數據集中有400個觀測值，每個樣本有25個屬性項，其中14個是線性值類別屬性項，11個是連續數值屬性項，目標類是二元指示器，表征患者是否患有慢性腎病(ckd表示患有慢性腎病，notckd表示不患有慢性腎病)。皮膚病數據集中有366個觀測值，每個樣本具有35個屬性項。其中，34個是線性類別屬性項，1個年齡屬性是連續屬性項，目標類為6種可能的疾病類型。

4.1 數據預處理

實驗中，當對年齡區間進行離散化時，遇到的問題是如何確定區間的寬度。如果區間過寬，會因為缺乏置信度而丟失部分關聯模式；如果區間過窄，會因為缺乏支持度而丟失部分關聯模式；如果區間寬度定為10歲，將會導致某些置信度低于閾值，或者某些支持度低于閾值。因此，研究采用分位數離散化(Quantile Discretizer)將連續型數據轉換成分類型數據。

對于連續屬性項類別數目，研究中是依據已有特征屬性項目的分類的最大值確定。因此采用6個類別來劃分各屬性值，詳見表1。例如，年齡屬性([2, 90])通過字典序排序后，取用戶數目的6個百分位數分成6個區間，即{(2, 34], (34, 46], (46, 54], (54, 60], (60, 67], (67, 90]}，確保轉換后的年齡特征的類別平衡性。

實驗使用的皮膚病數據集見表2，年齡屬性項采用6個類別進行離散化處理，即(0, 21], (21, 29], (29, 36], (36, 43], (43, 52], (52, 75]，確保轉換后的年齡特征的類別平衡性。

表1 實驗所使用的慢性腎病數據集

表2 實驗所使用的皮膚病數據集

4.2 CKD數據集頻繁項集及關聯規則挖掘

研究設定數據集中最后一列為目標類(ckd=患病，notckd=未患病)，也就是分類關聯規則的后件，實驗的最小支持度minsup=0.15，最小置信度minconf=0.6，挖掘出最大的頻繁k=13項集數量為3個，由此產生的關聯規則模式見表3(截取前6個強關聯規則模式)。

表3 CKD數據集關聯規則模式

Tab. 3 Association rule patterns for chronic kidney disease data sets

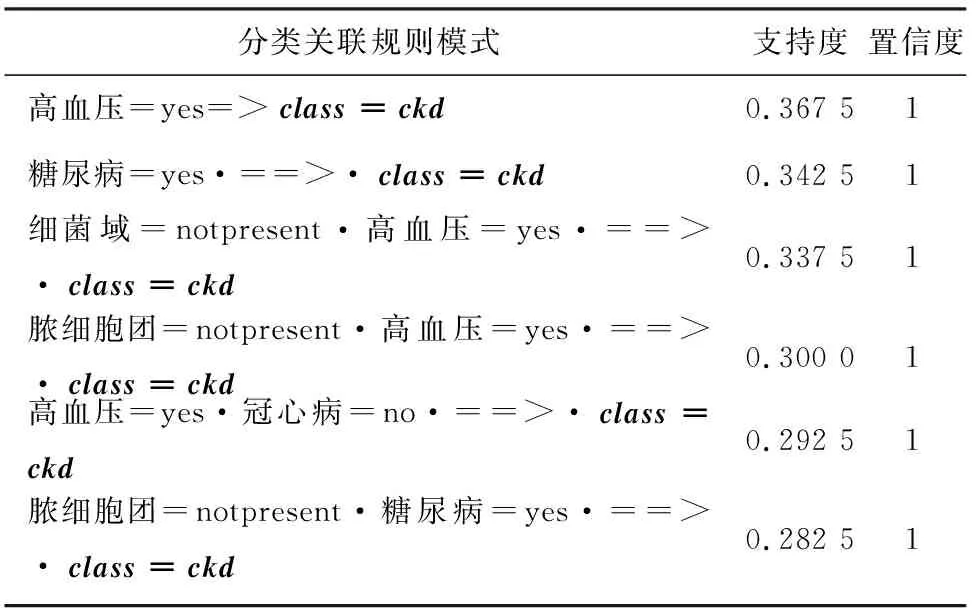
分類關聯規則模式支持度置信度高血壓=yes=>class=ckd0.367 51糖尿病=yes·==>·class=ckd0.342 51細菌域=notpresent·高血壓=yes·==>·class=ckd0.337 51膿細胞團=notpresent·高血壓=yes·==>·class=ckd0.300 01高血壓=yes·冠心病=no·==>·class=ckd0.292 51膿細胞團=notpresent·糖尿病=yes·==>·class=ckd0.282 51

由表3可知，當用戶患有高血壓疾病時，患有慢性腎病的支持度為36.75%，置信度為1；當用戶患有糖尿病時，患有慢性腎病的支持度為34.25%，置信度為1；當這兩種疾病與其它個人健康數據狀況并發發生時，支持度略有下降。關聯規則模式中另外一條記錄(高血壓=yes 糖尿病=yes ==> class=ckdsup:0.265conf:1)，表示同時患有高血壓和糖尿病的患者罹患慢性腎病的樣例共有106例，置信度為1。此實驗的研究結果與慢性腎病權威機構NIDDK提出的影響因素完全吻合[10]。因此，如果一名患者滿足上述條件，那么該患者就有極大的可能性發展成為慢性腎病，對個人健康的影響風險巨大。針對此情況，患者要做好預防慢性腎病的準備。通過對分類關聯規則模式和規律的分析，就可以挖掘有意義的信息來評價患者的身體狀況。通過研究結果，最終揭示慢性腎病致病因素與個人健康數據狀況的關聯關系，要控制并發癥的產生，防止疾病進一步惡化的情況出現，使患者能夠及時接受治療，為用戶健康提供科學的服務推薦方法。

4.3 皮膚病數據集頻繁項集及關聯規則挖掘

研究中,設定數據集中最后一列為目標類(銀屑病=1，皮脂性皮炎=2，扁平苔蘚=3，玫瑰糠疹=4，慢性皮炎=5，毛發紅糠疹=6)，即關聯規則的后件，本文中實驗的最小支持度minsup=0.15，最小置信度minconf=0.6，挖掘出最大的頻繁k=14項集數量為1個，由此產生的關聯規則模式見表4。截取6個強關聯規則模式，其中2個分類關聯規則模式的目標類為“皮脂性皮炎=2”和“扁平苔蘚=3”。

表4 皮膚病數據集關聯規則模式

由實驗可知，銀屑病(class=1)的關聯規則模式數量遠大于其它類型皮膚病關聯規則模式的數量。以表4中第一條數據為例，若某個皮膚病患者的臨床癥狀滿足“多邊形丘疹=0，乳頭狀真皮纖維化=0，胞吐=0，海綿水腫=0，濾泡性角插頭=0”，那么該患者的皮膚病類型為銀屑病的支持度為25.41%，置信度為1。因此，如果一名皮膚病患者滿足上述條件，那么就有極大的可能性是患有銀屑病類型的皮膚病，醫生會根據銀屑病的臨床癥狀與疾病特點，對患者對癥下藥。通過對皮膚病關聯規則模式和規律的分析，可以挖掘出有意義的數據信息來對患者所屬的皮膚病類別加以區分，針對疾病的特點進行治療，為患者提供個性化的服務推薦方法。

4.4 算法性能評估

本節將討論算法的性能。首先研究在不同最小支持度和最小置信度下的算法運行時間，如圖2所示。2個數據集實驗結果顯示，最小置信度的變化對運行時間的性能影響不大，但是當最小支持度變小時運行時間會呈指數級增長。

對于構建的關聯規則數量，如圖3所示，關聯規則的數量與運行時間的情況類似，都是隨著最小支持度的降低，而呈現指數級的增長。

頻繁項集的數量，只與最小支持度有關，與最小置信度無關，如圖4所示。頻繁項集的數量也是隨著最小支持度的降低成指數級增長。這些實驗結果表明，最小支持度，也就是項集的反單調性，對剔除非頻繁項集是非常有效的。

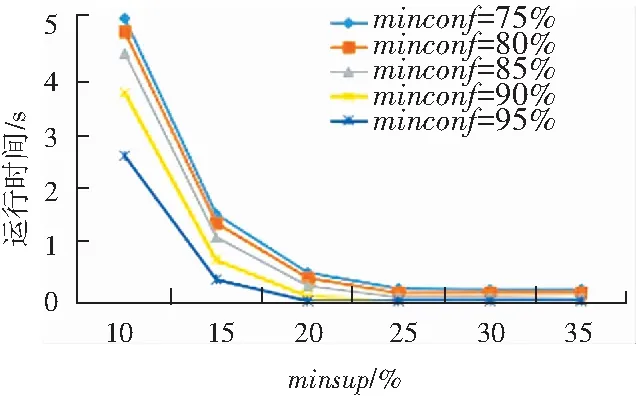
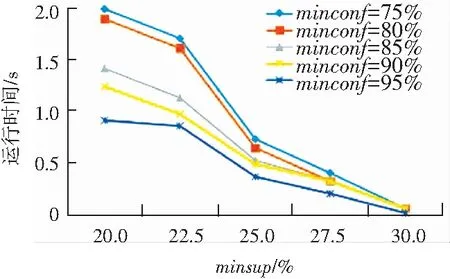
圖2 不同最小支持度和最小置信度的運行時間

Fig. 2 Running time with different minimum support and minimum confidence

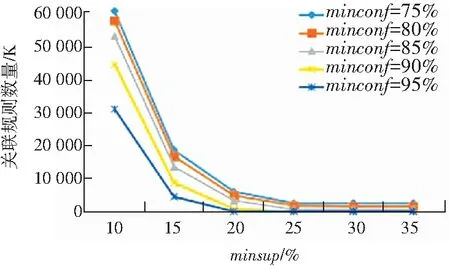
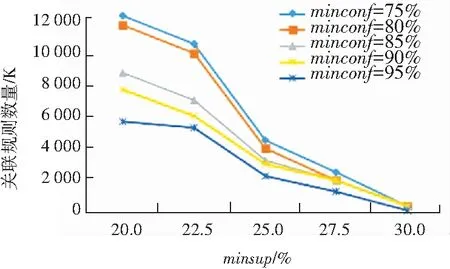
圖3 不同最小支持度和最小置信度的關聯規則數量

Fig. 3 Number of association rules with different minimum support and minimum confidence

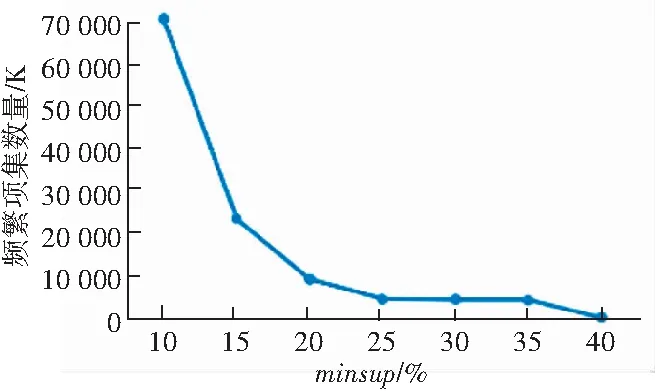
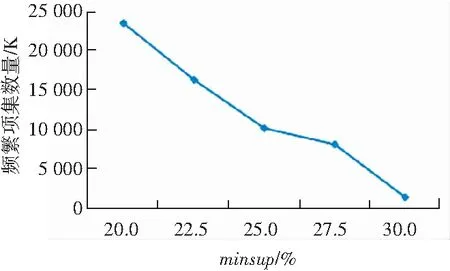
圖4 不同最小支持度的頻繁項集數量

Fig. 4 Number of frequent itemsets with different minimum supports

綜上所述，如果最小支持度minsup較高，比如達到30%，此時就可以用較短的運行時間獲得較少而有意義的關聯規則，當然其中的很多規則可能是平凡的。如果為了挖掘更有意義的關聯規則模式，可以采用較小的最小支持度，但這會導致無法接受的系統運行時間和指數級關聯規則和頻繁項集。因此采用合理的、可接受的最小支持度和最小置信度的值，是非常必要的。

5 結束語

本文提出從數據的隱式特征中識別出數據間的分類關聯規則模式，通過支持度和置信度的權衡保證分類關聯規則模式的有效性。基于關聯分析的算法，對數據內在特征的分類關聯規則模式進行挖掘，實現了個人健康數據的分解及分類，挖掘出數據的頻繁項集，發現致病因素的重要數據特征，對個人健康特征的疾病預防與推薦具有重要的指導和建設性意義。