參差不齊怎么學

王加林

【摘要】在平時的教學中，學生的學情差異經常會給教師的教學帶來困擾。如何能讓不同層次的學生在課堂學習中都學有所得、學有所長，是教師必須要思考的。本文以蘇教版數學三年級下冊“兩位數乘兩位數（筆算）”為例，談一談如何在參差不齊的學情之間進行差異化的分層設計，從課前預設、課中理學、課末思辨三個環節去落實差異化教學。

【關鍵詞】差異化學習 分層設計 數學

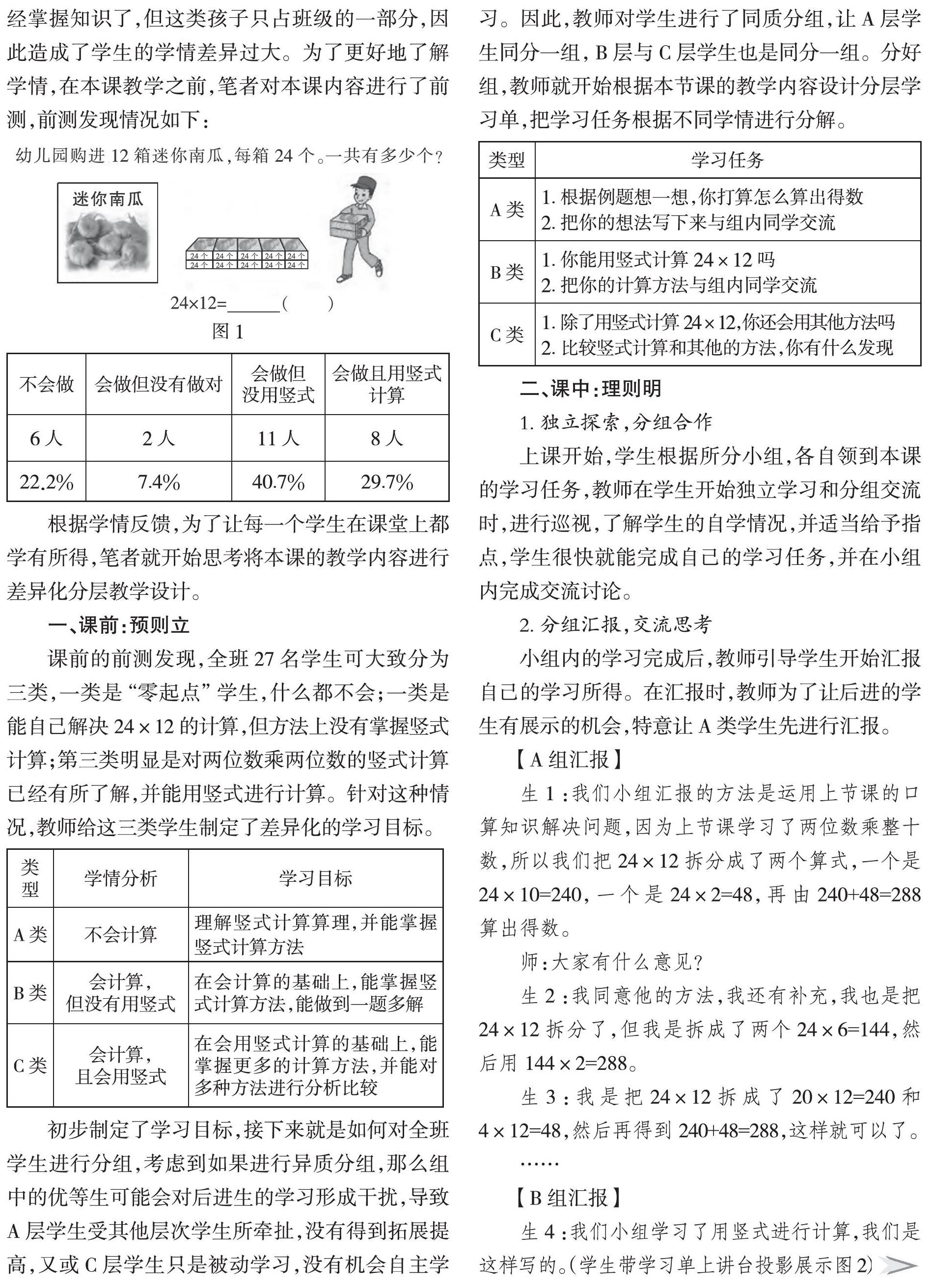
“兩位數乘兩位數（筆算）”是蘇教版數學三年級下冊第一單元第二課時的教學內容，本課教材中創設了幼兒園購南瓜的情境。（圖1）

筆者所在小學為南京市生源較好地區，存在部分家長有幫助孩子提前學習或讓孩子上輔導班的情況，所以往往沒有開始課堂教學，學生就已經掌握知識了，但這類孩子只占班級的一部分，因此造成了學生的學情差異過大。為了更好地了解學情，在本課教學之前，筆者對本課內容進行了前測，前測發現情況如下：

根據學情反饋，為了讓每一個學生在課堂上都學有所得，筆者就開始思考將本課的教學內容進行差異化分層教學設計。

一、課前：預則立

課前的前測發現，全班27名學生可大致分為三類，一類是“零起點”學生，什么都不會;一類是能自己解決24×12的計算，但方法上沒有掌握豎式計算;第三類明顯是對兩位數乘兩位數的豎式計算已經有所了解，并能用豎式進行計算。針對這種情況，教師給這三類學生制定了差異化的學習目標。

初步制定了學習目標，接下來就是如何對全班學生進行分組，考慮到如果進行異質分組，那么組中的優等生可能會對后進生的學習形成干擾，導致A層學生受其他層次學生所牽扯，沒有得到拓展提高，又或C層學生只是被動學習，沒有機會自主學習。因此，教師對學生進行了同質分組，讓A層學生同分一組，B層與C層學生也是同分一組。分好組，教師就開始根據本節課的教學內容設計分層學習單，把學習任務根據不同學情進行分解。

二、課中：理則明

1.獨立探索，分組合作

上課開始，學生根據所分小組，各自領到本課的學習任務，教師在學生開始獨立學習和分組交流時，進行巡視，了解學生的自學情況，并適當給予指點，學生很快就能完成自己的學習任務，并在小組內完成交流討論。

2.分組匯報，交流思考

小組內的學習完成后，教師引導學生開始匯報自己的學習所得。在匯報時，教師為了讓后進的學生有展示的機會，特意讓A類學生先進行匯報。

【A組匯報】

生1：我們小組匯報的方法是運用上節課的口算知識解決問題，因為上節課學習了兩位數乘整十數，所以我們把24×12拆分成了兩個算式，一個是24×10=240，一個是24×2=48，再由240+48=288算出得數。

師：大家有什么意見？

生2：我同意他的方法，我還有補充，我也是把24×12拆分了，但我是拆成了兩個24×6=144，然后用144×2=288。

生3：我是把24×12拆成了20×12=240和4×12=48，然后再得到240+48=288，這樣就可以了。

……

【B組匯報】

生4：我們小組學習了用豎式進行計算，我們是這樣寫的。（學生帶學習單上講臺投影展示圖2）

首先要把兩個乘數像這樣相同數位對齊，然后先用24×2=48，得數寫在這里，然后再用24×10=240，得數寫在下面一行，要注意相同數位對齊，最后把48和240相加，得數是288。

師：大家有什么看法？

生5：我同意他的方式，但是有一個地方我和他不一樣，就是24×10=240，我們可以把它看作是24×1=24，然后把2寫在百位，4寫在十位，個位上不用寫，最后把48和240相加得288。（圖3）

師：你這樣寫的原因是什么？

生5：我覺得這樣更簡便。

師：是的，一般情況下，我們確實可以把24×10=240后面的0省去，這樣寫起來要簡單，不過要注意，這里的24是24個十，不是24個一，相同的數位要對齊。

【C組匯報】

生6：我們小組同學都已經會用豎式計算了，所以我們就討論了24×12還有沒有其他的方法。我給大家介紹一種24×12的算法，這種方法是我上輔導班的時候學到的。（圖4）

你們看，只要先畫上這樣的格子，然后把兩個乘數分別寫在格子的上面和右邊，用一個上面的數和一個右面的數相乘，把乘的結果填寫在對應的格子里就可以了，比如4×2=8，就寫在右下角的格子里，但8是一位數，所以我們就寫成08就可以了，最后像這樣把得數斜著相加，得到0288，就是288。

生7：他的方法我聽過，就是我國古代的“鋪地錦”算法，我們書上后面有，我還有一種書上沒有的方法，叫畫線法，是我爺爺教給我的。（圖5）

先把24像這樣畫成兩組橫線，再把12像這樣畫成兩組豎線，橫線和豎線交叉后會有點，然后斜著把這相交點數相加，這樣我們就得到了三個數，分別是2、8、8，合起來就是288，也就是答案了。

我們發現，分組后每個小組的學生都在自己力所能及的范圍去探索兩位數乘兩位數的算理和算法，這節課上的同質分組也恰好避免了不同層次學生之間在小組內學習時的互相影響，同時在分組匯報時，又能學習到其他小組學生的不同想法，基本上對兩位數乘兩位數的算法進行了匯總與整理。

三、課末：思則進

數學是一門思維學科，數學的學習也絕不只是為了學會各種計算的方法，數學的學習更重要的是發展數學思維，接下來，教師根據學生展示的各種算法，提出了問題：“同樣是24×12這樣一道乘法算式，同學們就有這么多不同的算法，那老師想問問大家，這些不同的方法之間有聯系嗎？先在小組里討論，然后匯報。”

學生小組討論后，各自發表了自己的思考與發現。

生8：我發現第1種算法和豎式計算其實是有聯系的，你們看豎式計算（圖3），這里的48，其實就是把24×12拆成兩部分，先計算24×2=48，這里的240，其實就是另一個部分24×10=240，然后把48和240加起來得288。這兩種算法的道理其實是一樣的，都是把其中的一個乘法拆成一個整十數和一個一位數，分別相乘再相加。不同的是形式不一樣。（圖6）

師：你們同意嗎？那把豎式中24和12換個位置，你能說一說每一步的意思嗎？

學生計算，并說算理。（圖7）

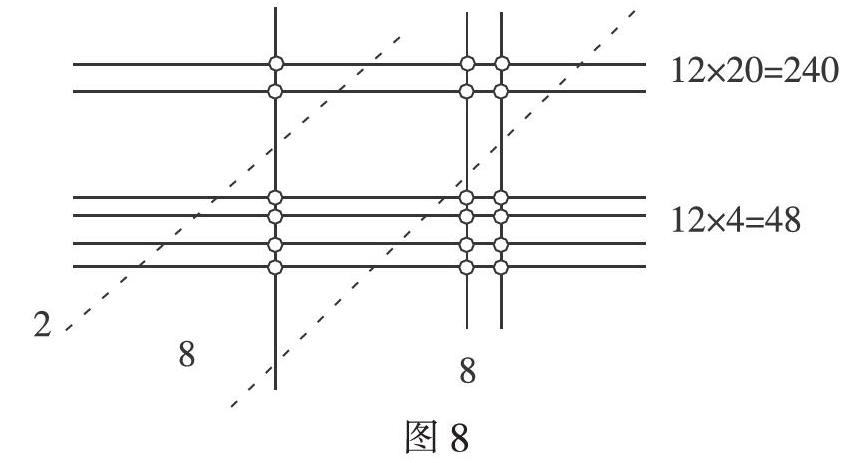
生9：我還發現其實畫線法和豎式計算也有聯系，你看畫線法計算有許多交點，下面的交點就表示48，是12×4所得;上面的交點表示240，就是12乘20所得;最后用兩道斜虛線把這些交點分成三個部分，其實就是表示相同數位要對齊，然后再相加，得到288。（圖8）

生10：老師，我發現“鋪地錦”算法中的斜線和畫線法的斜線也是同樣的作用，就是把相同數位上的數對齊，比如2×4所得的8就在個位，4×10所得的40，和2×20所得的40都是在十位，20×10所得的200在百位。

生11：老師，我可以總結一下嗎？我發現，其實今天學習的兩位數乘兩位數方法很多，但它們的算理是有聯系的，都是把其中一個乘數拆開，分別和另一個乘數相乘，然后把兩次相乘的得數再相加，不同的是方式不一樣，我們一般會用豎式進行計算，這樣又清楚又快速，當然用“鋪地錦”和畫線法也是可以的，只不過會麻煩一點。

生12：老師，我還有發現，我們以后會遇到一些復雜的問題，我們只要想辦法把它拆成我們學習過的簡單的問題就可以解決了。比如我發現兩位數乘兩位數的乘法比以前的兩位數乘一位數要復雜。但是，我們可以把兩位數乘兩位數拆成我們學過的兩位數乘一位數和兩位數乘整十數，然后再把得數相加就可以了。以后我們還要學習三位數乘兩位數、三位數乘三位數，我們也只要把它們拆成三位數乘一位數和三位數乘整十數、整百數，最后相加就可以了。

師：對，今天這節課，看來同學們的收獲真多，不但掌握了兩位數乘兩位數的算理和算法，還發現了不同算法之間的聯系，更重要的是，同學們還發現數學學習的一個重要方法，就是轉化策略，遇到一些沒有學習過的復雜問題，我們可以把復雜問題轉化成一些簡單的問題。只要明白道理，理清思路，我們就能解決問題。

綜上，我們知道學生之間的學情差異是客觀存在的，在一些特殊情況下這種學情差異可能會加大，也會對數學課堂教學造成影響。為了讓每一個學生都能在每一節課上得到應有的發展，差異化的分層教學勢在必行。這就需要教師能科學地分析班級學情，在學情基礎上，根據教材內容對學習任務進行分層設計，并能讓不同層次的學生在學習中真真切切地參與到學習中來，讓學習在每一個學生的身上真實發生，這才是真正有意義的學習。