以“情景”促興趣　以“變式”促提升

伍尚燕

“情景與變式”就是在課堂中為要學習的知識創(chuàng)設情景，使學生明白知識的發(fā)生過程，并在熟練掌握知識之后能對知識進行變式運用。知識發(fā)生過程，可以是引入該知識的原因，也可以是積累從實際情景中提煉數(shù)學模型的經(jīng)驗等。“變式運用”，即對知識運用能舉一反三，一般通過變更情景、變更條件、變更結論對知識進行拓展運用來實現(xiàn)。下面來談談如何通過創(chuàng)設“情景與變式”，來提高學生的學習興趣，調(diào)動學習積極性，提高課堂效果。

一、以“情景”促興趣

《數(shù)學新課程標準》指出：數(shù)學教學要緊密聯(lián)系學生的實際，從學生的生活經(jīng)驗和已有知識出發(fā)，在新知引入階段、新知建構階段、知識運用階段，創(chuàng)設各種情景;為學生提供從事數(shù)學活動的機會，激發(fā)學習數(shù)學的興趣和提高學生的創(chuàng)新能力，打造數(shù)學高效課堂。

（一）新知引入階段設趣味性情景

在新知引入階段我們可以根據(jù)教學內(nèi)容的需要，引用與學生生活息息相關的故事、動畫、謎語、歌曲、游戲、詩歌等生活情景，把學生的注意力、好奇心吸引住，激發(fā)學生學習的積極性。

如五年級上冊“分數(shù)的基本性質(zhì)”的情境引入如下。

課件演示：一天，唐僧化緣得了三個一樣大小的餅，望著那香噴噴的餅，孫悟空和豬八戒饞得口水直流。唐僧把第一個餅平均分成2份，給了大師兄悟空1份; 第二個餅平均分成4份，給了沙和尚2份;豬八戒更貪心啦，對師父說：“我要4份，我要4份。”唐僧又把第三個餅平均分成8份，給了豬八戒其中4份。同學們猜猜悟空、八戒、沙僧三人哪個分得多？

學生聽后，紛紛發(fā)表自己的意見。

師：聰明的唐僧是用什么方法來滿足三人的要求，又分得那么公平呢？

把數(shù)學知識蘊藏在有趣的故事中，不僅激發(fā)了學生的學習興趣，更讓學生在故事中體驗數(shù)學思想，有效地增進了課堂教學效果，為打造高效課堂奠定基礎。

（二）新知建構階段創(chuàng)設動手實踐的情景

在新知建構階段創(chuàng)設動手實踐的情景，讓學生在操作中建立數(shù)學模型，領悟知識的本質(zhì)。

如教學“1000以內(nèi)數(shù)的認識”一課，為了讓學生掌握數(shù)數(shù)的方法，我設計了一個動手數(shù)一數(shù)、填一填的教學情景。

師：老師送給每個小組一份禮物，猜一猜是什么？

師：禮物就在組長的抽屜里，請小組長拿出來。

生：是小棒。

師：對，是小棒。禮物里既有單根小棒，也有1小捆，還有大捆的？那你們知道1小捆里有多少根嗎？請同學們小組合作，把這些小棒數(shù)一數(shù)，算一算，怎樣能又準又快地數(shù)出來，并填寫小實驗。

小實驗

通過數(shù)數(shù)我發(fā)現(xiàn)：

一個一個地數(shù)，10個一是（ ?），

一十一十地數(shù)，10個十是（ ?），

一百一百地數(shù)，10個一百是（ ?）。

用生活中司空見慣的“數(shù)小棒”入手，創(chuàng)設動手操作的情景，將學生引入這堂課的重點：相鄰計數(shù)單位之間十進制的關系。這樣一來，巧妙地把一些枯燥而抽象的數(shù)學規(guī)律變得生動有趣，使他們在愉快，和諧的課堂氛圍中突破了知識的難點。

（三）知識運用階段創(chuàng)問題情景

知識運用階段創(chuàng)問題情景可以給學生帶來“數(shù)學有用，數(shù)學可以解決生活問題”的體驗感和愉悅感。因此老師要基于學生的學習規(guī)律設計多層次的認知挑戰(zhàn)，可以是有關記憶的、理解性的、探究性的。讓學生對應模型，再回歸到現(xiàn)實生活問題解決的開放過程。

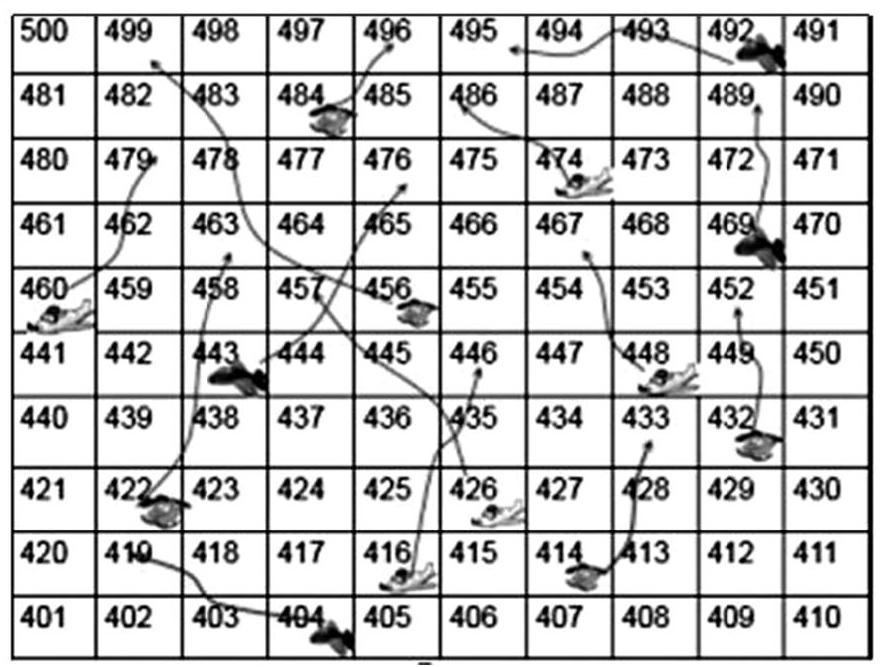
如《1000以內(nèi)數(shù)的認識》練習，我設計了一個跳飛機游戲。

師：課前我們已經(jīng)玩了1到100以內(nèi)數(shù)跳飛機的游戲，現(xiàn)在我們再來玩從500開始跳到1000的游戲，看哪個小組的同學跳得又快又準確。

跳飛機游戲規(guī)則：1.先擲骰子，確定點數(shù)。2.根據(jù)點數(shù)，讀出棋子經(jīng)過的數(shù)字。3.如果遇到飛機則按路線飛行。

課的結尾學生注意力相對比較散漫，這時老師就要設計能吸引學生注意力的情景，這樣既讓學生從情景中捕捉到數(shù)學信息，又用數(shù)學知識去解決了身邊的問題，提高了學生數(shù)學學習能力和應用能力。

在課堂教學的新知引入、建構、運用等環(huán)節(jié)創(chuàng)設情景，做到以情育人、以景導學;既讓學生體驗了“知識源自生活，知識源自情景”，又激發(fā)了學習興趣、提高教學效果。

二、以“變式”促提升

通常，在課堂中每學了一道例題或解答了一道題的答案，我們都可以理解為“完成了”，就是說對于該題的任務就結束了，其實不是的。假如做完一道題后，老師引導學生在此基礎上再多走一步，收獲將是倍增的，這一步就是變式訓練。變式訓練可以是對問題的變式、對條件的變式，也可以是對問題、條件同時作較深層面修改的變式;一般條件變式有以下類型。

（一）條件數(shù)據(jù)的修改

這是一年級一道連加的計算題，顯然是考查學生對“三個數(shù)合并成一個數(shù)的運算”方法的運用。變式：把題中第二、三個數(shù)據(jù)“3”“1”，分別修改為“2”和“2”。改動之后，計算對比，一方面鞏固了4的組成，“4可以分成3和1”“4可以分成2和2”。另一方面，也讓學生直觀地感知了“一個加數(shù)增加1，另一個加數(shù)減少1，結果不變”的現(xiàn)實。數(shù)字的變化，既訓練了學生做題、審題時認真的態(tài)度，同時也提高了學生的觀察能力。

（二）條件次序的修改

再來把上面題目進行變式：把數(shù)據(jù)一與數(shù)據(jù)二對調(diào)位置，看似簡單甚至無必要，其實不然。解題時，學生經(jīng)過計算對比發(fā)現(xiàn)，加數(shù)位置對換后，計算結果不變這一現(xiàn)象，為以后學習加法交換律提供了淺層表象，積累下了感性的現(xiàn)實認知。

（三）條件的補充

題目要訓練的是讓學生把分步算式整合成綜合算式的能力。變式：把條件2中的“5”隱去，用方框代替。這樣的改變是讓學生注意到，第二步的計算要用到第一步計算的結果。這樣改變更重要的是，它的“一弱化一強化”的作用，就是說第一步的計算結果在綜合算式里不顯示的，強化的是2、3、4三個數(shù)據(jù)在綜合算式的出現(xiàn)。

本題的變式帶有開放性，圈去的不同，剩下的就不同，條件變了，所求問題的結果就變了。當然，這個條件得由學生自己補充。最后可以追問一句“我一個都不圈，第二步應減去什么”。這樣的變式培養(yǎng)了學生的思維能力和創(chuàng)新能力。

（四）條件的延伸

這是四年級下冊的題目，是一道開放題，學生會有難度。題中有兩個標價，一個總價，問最多可以買到多少件？還剩多少錢？解決這個問題，學生要用到總價、單價和數(shù)量三者間的數(shù)量關系式。更為重要的是，它的解題過程還要策略方面的思考，進行策略的選優(yōu)。

兩種標價就有兩種單獨的買法，考慮到“最多”還有一綜合的買法。對比發(fā)現(xiàn)“多買合算”這一普遍的交易現(xiàn)象。提煉方法：先兩件兩件的買，再用剩余的錢一件一件的買，能買到最多。

變式：從原條件中延伸出第三個條件“65元/3件”。

有了前面的基礎，同學們會首先把三個標價作對比，找出合算的買法，三件三件的買——兩件兩件的買——一件一件的買。這樣的變式訓練，錘煉了技能，提升了方法。

可以把變式的主動權交給學生，讓學生自己思考如何把題目進行變式，如何解答。數(shù)學變式訓練無時不在，在教學過程中，教師要加強知識的整合，系統(tǒng)的優(yōu)化，能力的拓展，讓學生真正實現(xiàn)一題一得，一題多得，融會而貫通。

以上是對“情景與變式”提高課堂效率的一點見解，在教學工作中我們要做一個“情景與變式”的有心人，通過以“情景”吸引學生學習興趣、以“變式”提升課堂教學效果。

責任編輯 錢昭君