基于SARIMA模型的月徑流量預測
賀依韜 馬騰


摘? 要:徑流量預測是水文學研究的重要方向之一,開展徑流預測,對于區域水資源的綜合開發利用、合理配置、高效管理具有重要的指導作用。徑流序列可以視為典型的時間序列,SARIMA模型是一種常用的時間序列模型,能夠間接考慮其他相關隨機變量的變化,建模高效、便捷。該文在某水文站30年歷史月徑流量分析的基礎上,建立SARIMA模型對該水文站未來18個月的徑流量進行預測,預測結果的確定性系數為0.8594,預測精度較高,對于該區域的水文工作的開展具有重要的現實意義。
關鍵詞:徑流預測? 時間序列? SARIMA模型? 模型評價
中圖分類號:TV214 ? ?文獻標識碼:A 文章編號:1672-3791(2020)02(c)-0042-03
數據驅動模型不以水文過程作為模型建立的基礎,而是著重于數據關系的分析,建模方便高效,預測精度高。常見的數據驅動模型有多元回歸分析、時間序列分析、神經網絡等。其中多元回歸分析預報因子選擇困難,對預測精度影響較大,神經網絡需要數據量大,預測結果不穩定。時間序列模型通過少量數據就可做出精確的短期預測,因而被廣泛應用,其中SARIMA模型是一種考慮到序列周期變化的時間序列建模方法。某一觀測或統計數值按其發生的時間先后順序形成的數列稱為時間序列[1]。水文觀測值按期觀測時間形成的數列是一種典型的時間序列[2]。
該文在水文時間序列分析的基礎上建立SARIMA模型對某水文站歷史月徑流量進行擬合,選擇最優模型對未來一段時間的月徑流量進行預測,以期為該地區水文工作提供參考。
1? 研究方法
對于平穩時間序列[4],一般可對其建立自回歸滑動平均ARMA(p,q)模型,它是自回歸AR(p)模型和移動平均MA(q)模型的組合,其模型的基本形式如式(1)。
yt=c+1yt-1+2yt-2+...+pyt-p+et+θ1et-1+θ2et-2+…+θqet-p? ? (1)
式(1)中,yt為時間序列第t時刻的觀察值;yt-1,yt-2,…,yt-p為時序yt的滯后序列;et,et-1,et-2,…,et-q為模型在第t期,第t-1期,…,第t-q期的誤差;1,2,…,p,θ1,θ2,…,θq為待估計參數;c為常數項。
ARIMA(p,d,q)模型是ARMA模型的變換形式,其中d表示原始序列經過d次差分后轉化為平穩時間序列。某些時間序列中,存在明顯的周期性變化,這些周期是由于季節性變化(包括季度、月度等變化)或一些外部因素引起的,這類序列稱為季節性序列。對時間序列經過有限次差分和季節差分,將隨機誤差的長久影響變成暫時影響,將其轉化為平穩時間序列,在此基礎上建立季節性差分自回歸滑動平均SARIMA(p,d,q)×(P,D,Q)s模型。
考慮到水文站月徑流量的影響因素眾多,流域下墊面條件復雜,建立過程驅動模型所需數據較多,因此在其徑流特性分析的基礎上考慮對其建立時間序列模型并對其徑流量進行預測。
2? 實例分析
該文收集了某水文站1987年1月到2018年6月共計378個月的徑流量資料,使用1987年1月到2016年12月共30年360個月的流量數據作為訓練數據,使用2017年1月到2018年6月共18個月的流量數據作為校驗數據,通過對訓練數據進行分析處理并建立SARIMA模型。最終把預測值和期望值進行比較并評定預測精度。
2.1 實驗數據預處理
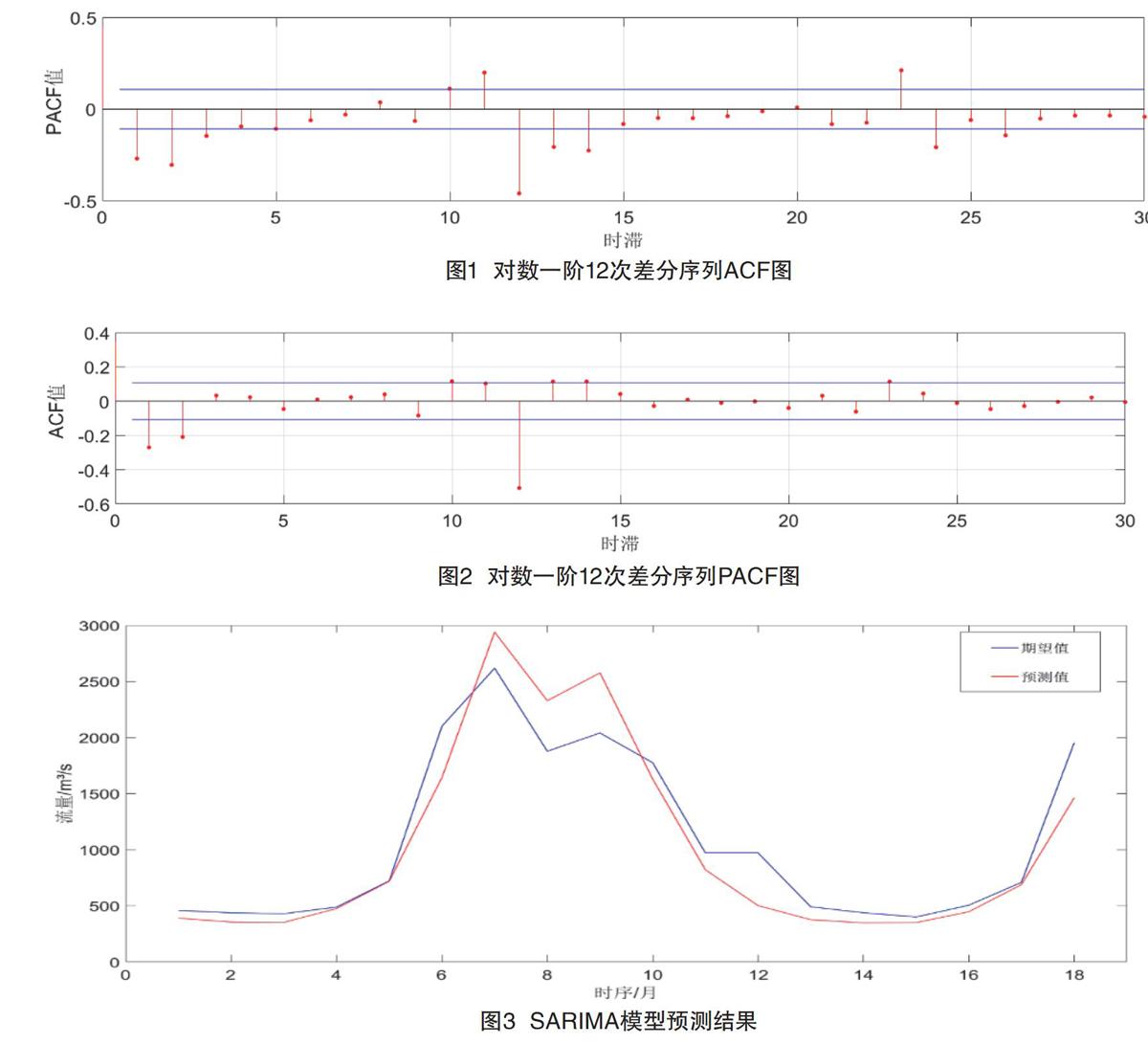
原始數據存在明顯的以12個月為周期的波動性并且不同時刻波動浮動差異較明顯,不滿足時間序列建模的必要條件。所以,考慮對原始數據進行對數一階12次差分變化,以減小原始數據的波動性和趨勢性。繪制變換后序列的自相關和偏相關圖,從自相關圖和偏自相關圖觀察該序列近似為一個平穩過程且為非白噪聲序列,滿足時間序列建模的要求。
2.2 模型識別和參數估計
根據自相關圖和偏相關圖的拖尾性和截尾性進行初步的模式識別。在初步識別的基礎上,建立可能的模型,通過最小二乘法估計其模型參數并計算統計量P值如表1所示,P值越小表示模型參數越顯著,其中紅色標出的參數的P值不顯著為零(一般當P值小于0.05則認為該參數顯著),其中模型6,8的所有參數都顯著。在所有參數都顯著的模型中,根據AIC值和SBC值進行模型優選,AIC和SBC值越小代表模型的效果越優良。
在模型6、8中,模型8的AIC值和SBC值均最小,所以模型8為所求的最優模型,其模型表達式為:
yt=0.5208yt-1+0.4625yt-2-0.8253yt-12-0.9994et-2-0.9155et-24 (2)
2.3 模型檢驗
對模型擬合值殘差進行白噪聲檢驗,殘差序列的自相關系數和偏自相關系數基本都在二倍置信區間內,通過計算殘差序列的P值全部大于0.05,沒有拒絕假設性實驗,相關系數與基本與零沒有顯著差異,該序列可被看作是白噪聲序列,說明模型擬合效果較好,信息提取較充分。
2.4 模型預測
模型建立完畢后,將訓練數據輸入模型。除個別峰值處整體擬合效果比較理想,對2017年1月到2018年6月的徑流量進行動態預測,預測結果見圖1。
2.5 預測精度評定
對水文預報方案的有效性評定采用下列確定性系數dy進行。dy越大,方案的有效性越高。
(3)
(4)
(5)
式中,Se為預報的均方差;σy為預報要素值的均方差;yi為實測值;y為預報值;為實測系列的均值;n為實測系列的點據數。評定方案的有效性時按表4中標準進行。預報方案有效性達到甲(dy>0.90)、乙(dy處于0.70~0.90時)兩個等級時,方案可被用于作業預報;方案等級為丙等(dy處于0.5~0.69時)時,只可用作參考性預報;方案有效性低于丙等時不能用于作業預報,只能做參考性評估。
計算此次預測的確定性系數,得dy=0.8594,預報方案的有效性為乙等,說明該次預報效果較好,可用于作業預報。
3? 結語
該文在對某水文站30年歷年逐月徑流量序列分析的基礎上,建立了SARIMA模型對歷史徑流量進行擬合。利用建立的最優模型預測了2017年1月到2018年6月共18個月的徑流量。預測結果表明SARIMA模型在該水文站的月徑流量預測上有較好的效果,預測的確定性系數為0.8594,預報方案的有效性為乙等,可以用于作業預報。
參考文獻
[1] 李達.基于時間序列分析方法的油田產量預測與應用[D].蘭州理工大學,2018.
[2] 程揚,王偉,王曉青.水文時間序列預測模型研究進展[J].人民珠江,2019,40(7):18-23.
[3] 雷昌寧.基于SARIMA和SVR混合模型的黑河徑流量預測分析[D].蘭州大學,2018.
[4] 龍天瑋.平穩水文時間序列的極小值分布[D].重慶交通大學,2017.

