應屆大學畢業生發展方向前景分析模型

王瑞梅　張曉娜　張供送　任文宇

摘? 要：隨著當代社會教育領域的不斷發展，大學畢業生人數正在逐年遞增，其畢業后的發展方向也逐漸變得多樣化。若想預測大學畢業生各個發展方向的發展走勢，需要逐年收集調查大學畢業生的發展意向，利用MATLAB對上述數據進行聚類分析，得到A城市大學畢業生的主流發展方向。再對各類發展方向進行詳細數據收集，通過提取各年份的考研人數級考研率、就業人數、就業率等數據，建立年份與各發展方向的人數、人數與對應概率的回歸分析模型。以此分析預測A城市大學畢業生的發展方向前景。

關鍵詞：聚類分析? 一元回歸分析? 統計預測

中圖分類號：F27 ? ?文獻標識碼：A 文章編號：1672-3791（2020）02（c）-0215-04

隨著人口總數的不斷增加，應屆大學畢業生人數也在逐年增長。隨著當今社會對人才的日益重視，人們深切體會到了引進人才對于城市治理、經濟發展和高新技術產業的推廣具有十分重要的意義。然而，對于每年數以萬計的大學畢業生，正確預估其選擇趨勢與未來走向變得愈發重要。對大學畢業生的發展傾向提前做出相應預測，有利于各地人才市場及時對人力資源需求做出調整;有利于各高校對招生計劃進行改進;工廠企業對招聘要求進行完善，以保證各個城市更好地實施人才經營戰略，將人才利用率發揮至最大。該文將以A城市為例，通過統計近年來本市應屆大學畢業生畢業后的發展方向，構造A城市大學畢業生發展方向前景分析模型，對A城市大學生未來選擇進行分析預測。以便對該城市的工廠企業、高等院校等單位針對各年份變化趨勢與變化幅度做出相應調整，更好地應對人口增長帶來的畢業生人數逐年激增現象。

1? 問題解決過程

考慮到不同年份大學畢業生的人數不同，其畢業后各自的發展意向也存在較大差別，首先需要對A城市各年份應屆大學畢業生的發展意向進行隨機調查收集，將獲得的數據按照年份與發展方向進行分類，并將完成分類的數據導入制圖軟件。然后對數據進行無量綱化處理，剔除不符合要求的數據。再采用聚類分析的方法，利用MATLAB繪制出相應的圖像，通過分析圖像獲得近年來A城市應屆大學畢業生的未來發展方向分類，得到較為概括的分類結果。對分類處理后得到的幾個主要發展方向進行二次數據收集，通過提取各年份的出國人數及出國率、考研人數、及考研率、就業人數及就業率等數據，對年份與各發展方向的人數、人數與對應概率之間分別構建回歸分析模型，綜合兩個模型所得到的一元回歸方程來綜合評價A城市未來大學畢業生的發展前景走勢。

2? 建模求解

2.1 聚類分析

首先通過查閱網絡數據庫，搜集每年A城市應屆大學畢業生出國、考研考公、自主創業、外出就業等方面的數據。對獲取的數據進行初步處理，刪除數據表格的來源信息，排除錯誤數據，進行歸一化處理。將得到的數據輸入MATLAB，對數據進行聚類處理，得到圖1。

由圖1可得，A城市大學畢業生的主要發展意愿有3類，分別為上崗就業、攻讀碩士研究生學位和出國學習。

2.2 構建就業人數與就業概率的回歸分析模型

接下來對以上發展方向進行二次數據收集，通過提取A城市近幾年的總出國人數、出國率、總考研人數及考研率、總就業人數及就業率等數據，對其分別構建一元回歸分析模型。在此將以近年來畢業于A城市后傾向于在該市求職就業的大學畢業生為例，構建A城市年總就業人數與就業率的回歸分析模型。

首先收集由2006至2017年A城市應屆大學生就業人數和就業率的相關數據，將數據輸入制圖軟件繪制散點圖，可以看出A城市大學生就業人數與就業率之間存在線性關系（見圖2）。

2.2.1 構建一元回歸方程

設一元線性回歸的模型為y=β0+β1x+ε。其中β0、β1為回歸系數，ε為隨機誤差項，總是假設ε～N（0，σ2）。其中x代表A城市大學生就業人數，y代表對應就業率。

對x和y分別進行n次獨立觀測，得到以下n對觀測值：（yi，xi），i=1，2，…，n，且這n對觀測值之間符合一元回歸模型y=β0+β1x+εi，i=1，2，…，n（對于每次觀測，當i≠a時，εi與εa之間相互獨立）。

2.2.2 最小二乘法計算參數

令，則。

令，。

可得如下方程組：

求解此正規方程組可得回歸方程的最小二乘估計：

，。

將所得A城市大學生就業人數與就業率數據輸入MATLAB，使用regress與rcoplot函數進行編程得：=-0.118，=0.0112，A城市大學生就業人數與就業率之間的一元回歸方程為y=-0.118+0.0112x。

同時可得：的置信區間是[-0.4657，-0.1731]，的置信區間是[0.0014? 0.0021]。R2=0.8849，F=99.8964，P=0.00002，s2=0.0024。由于R2∈（0，1]，擬合優度可以解釋變異占總變異的百分比。

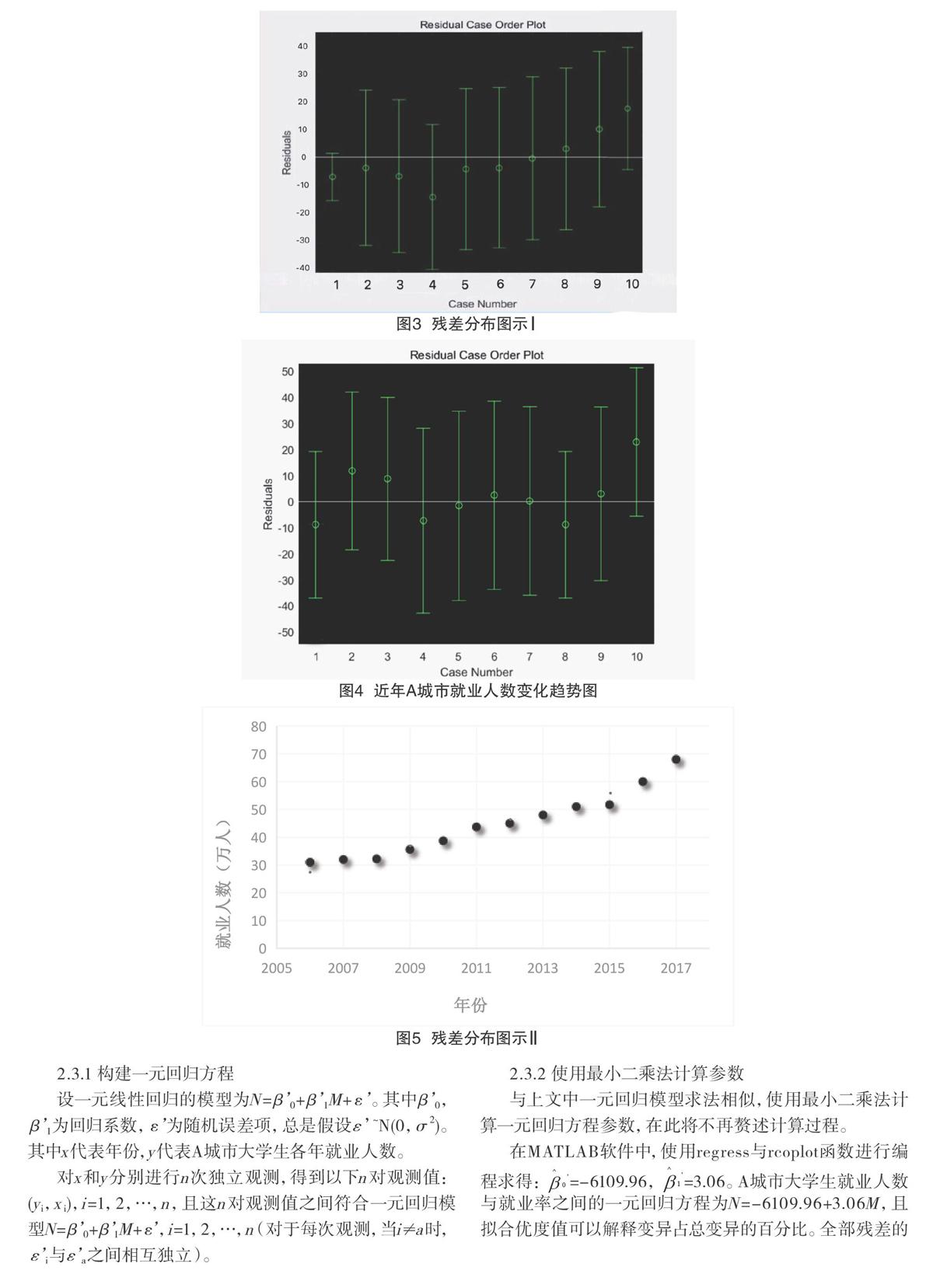
觀察由指令rcoplot（r，rint）繪制的殘差分布圖，全部殘差的置信區間均包含零點，此模型成立。

分布圖如圖3所示。

2.3 構建就業人數與年份的回歸分析模型

同構建就業人數與就業率的回歸分析模型步驟相似，首先提取A城市2006—2017年應屆大學生就業人數。使用制圖軟件繪制散點圖，分析所的圖像可以看出A城市大學生就業人數與其對應年份之間存在線性關系（見圖4）。

2.3.1 構建一元回歸方程

設一元線性回歸的模型為N=β0+β1M+ε。其中β0，β1為回歸系數，ε為隨機誤差項，總是假設ε～N（0，σ2）。其中x代表年份，y代表A城市大學生各年就業人數。

對x和y分別進行n次獨立觀測，得到以下n對觀測值：（yi，xi），i=1，2，…，n，且這n對觀測值之間符合一元回歸模型N=β0+β1M+ε，i=1，2，…，n（對于每次觀測，當i≠a時，εi與εa之間相互獨立）。

2.3.2 使用最小二乘法計算參數

與上文中一元回歸模型求法相似，使用最小二乘法計算一元回歸方程參數，在此將不再贅述計算過程。

在MATLAB軟件中，使用regress與rcoplot函數進行編程求得：=-6109.96，=3.06。A城市大學生就業人數與就業率之間的一元回歸方程為N=-6109.96+3.06M，且擬合優度值可以解釋變異占總變異的百分比。全部殘差的置信區間均包含零點，殘差分布圖如圖5所示，此模型成立。

3? 模型應用

將年份數據代入所得模型，可得預測未來5年A城市應屆大學畢業生就業人口數與就業率，對應數據如表1所示。

綜合參考以上兩步回歸分析所得到的大學畢業生未來就業人數預測模型，可以對未來A城市大學畢業生的就業人數與就業率進行預估。未來5年（2020—2024）A城市應屆大學畢業生就業人數依次為71.24、74.30、77.36，80.42、83.48萬人;相應就業率依次為67.98%、71.41%、74.84%、78.27%、81.69%。可以得出未來位于5年A城市工廠企業應以1.05%的增長率對招聘人員數量進行擴招調整，以此減緩由待就業人數過多帶來的就業壓力。同時合理利用充足的人才資源，提高工廠的年生產效益，發展企業的整體競爭實力等。

對于A城市應屆大學畢業生的其余主流發展方向（如考研、出國等），可采用與預測就業人數相同的方法進行數據估測。通過提取各年份的出國人數及出國率、考研人數及考研率等數據。對年份與各發展方向的人數、人數與對應概率之間分別構建回歸分析模型，綜合兩個模型所得到的一元回歸方程來綜合評價A城市未來大學畢業生其他發展方向的前景狀況，以此對A城市應屆大學畢業生發展方向的定位分析做出進一步完善。

4? 結語

對于建立A城市應屆大學畢業生發展前景定位分析模型，首先調查收集A城市各年份應屆大學畢業生的發展意向，將獲得的數據按照年份與發展方向進行分類。利用聚類分析的方法，將所獲數據導入MATLAB繪制聚類分析直方圖，由此得到近年來A城市應屆大學畢業生的未來發展方向分類。再對幾個主要發展方向進行詳細數據的收集，對年份與各發展方向的人數，人數與對應概率之間分別構建回歸分析模型，綜合兩步回歸分析，對A城市未來大學畢業生不同選擇的前景走向進行預測估計，以保證人才的最大化利用。

參考文獻

[1] 程曉榮，吳紫薇.基于多元線性回歸分析的人力資源需求預測研究[J].電腦迷，2016（6）：81-82.

[2] 陳森法.一類系統的建模方法 復合回歸分析[J].系統工程，1989（1）：21-24，71.

[3] 陳君濤.高校畢業生就業預測算法研究分析[J].現代信息科技，2019，3（12）：86-87，90.

[4] 第十二章回歸分析[EB/OL].（2015-09-02）[2019-02-17].https：//www.wenku.baidu.com/view/d7ac76e1a417866fb94a8e10.html.