概率論教學中如何分散難點
張艷偉 秦孝艷

摘要:在概率論的教學中能否恰當合理地運用“分散難點”的教學方法,是反映教師教學水平的一項重要指標,也是教好概率論的一種保障。文章通過在概率概念、概率計算、概率理論與概率教學結構的建構四個方面的教學中,論述如何運用“分散難點”的教學方法,展現了“分散難點”的教學方法在概率論教學與學習中的重要作用。
關鍵詞:概率論;教學;分散難點
中圖分類號:G642.4? ? ?文獻標志碼:A? ? ?文章編號:1674-9324(2020)15-0286-03
教學中能否恰當合理地運用“分散難點”的教學方法,是教師教好學的一種重要的教學方法與手段。因為再難的問題只要把難點分散就會變得容易,反之,再容易的問題把難點集中到一塊也將變成難的問題。因此在教學中要求教師小到一堂課、一個定理、一個概念,大到整個學科,都應恰當、合理的運用好“分散難點”的教學方法,從而獲得更好的教學效果。
概率統計作為現代數學的重要分支,在自然科學、社會科學和工程技術的各個領域都具有極為廣泛的應用。正是概率統計的這種廣泛應用性,使得它成為各類專業大學生的重要的數學必修課之一。不同于確定數學,概率論是研究隨機現象及其統計規律的數學學科。故在數學教學中,概率論是教師比較難教、學生比較難學的一門數學課程,所以在概率論的教學中能否恰當、合理的運用“分散難點”的教學方法,就顯得更為重要。下面從四個方面簡述在概率論教學中如何運用“分散難點”的教學方法。
一、“概率概念”教學中如何分散難點
在概率概念教學中分散難點,就是通過概率概念的產生、發展過程中所體現的數學思想方法以及數學概念的教學要求[掌握概念的內涵(定義),明確概念的外延(分類)]進行分散,構造教學結構,實施教學。
定義1(概率):設F是一事件域,在F上定義實值集函數P,對每一事件A∈F,函數值為P(A),如果它滿足如下三個條件:
定義中所體現的數學思想方法:①P(A)是事件A的單值實函數。②P(A)滿足非負性、規范性、可列可加性。③P(A)的定義域是事件域F。
在概率概念教學中,按以下三個順序分散講授:
1.描述定義。在概率論中事件的發生都是隨機的,但卻存在著統計規律,即每個事件發生的可能性的大小是客觀存在的、確定的。這樣我們就可以依據每個事件發生可能性的大小來研究隨機現象。我們把表示事件發生可能性大小的數,即事件A的單值實函數,稱為事件的概率(概率的描述定義)。
2.概率的性質。概率的描述定義雖闡明了概率的本質含義,但卻無法知道事件概率的確定值。為了求出概率的確定值,人們根據對隨機現象長期探究的實踐,總結出概率的統計定義與古典定義。在這兩個定義中,概率都具有非負性、規范性、有限可加性三條基本性質。
3.事件域。樣本空間Ω的子集(事件),不一定都是可測的,有時存在不可測的子集,即概率不存在的子集(事件),而概率論只需研究概率存在的事件,這樣我們就把概率存在的事件組成的集合稱為事件域。
綜上所述“事件概率”概念的教學結構為:描述定義→統計定義→古典定義→事件→概率定義(數學定義)。
二、“概率計算”教學中如何分散難點
在概率計算教學中分散難點,就是通過概率計算的方法中所體現的數學思想方法,進行分散,構造教學結構,實施教學。
古典概率計算中,一種重要求概率的方法就是利用排列組合求概率,它也是概率教學中的一個難點。在教學中對它我們可以這樣分散難點:復習歸納排列組合有關知識→學習在概率論中應用的主要類型→學習利用排列組合求概率的有關問題與方法,其教學結構如下:
1.排列組合有關知識。理論:加法原理與乘法原理。
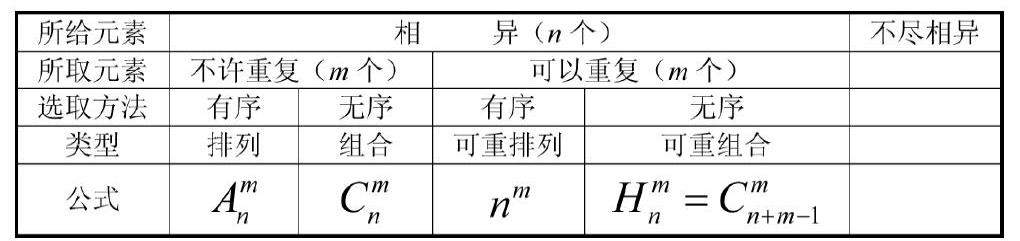
類型:
2.在概率論中應用排列組合的主要類型。
(1)抽球(樣)問題:從n個不同的球中,一次抽一個球。
①無放回地抽m個球,排成一排,有多少不同結果(排列問題)。
②無放回地抽m個球,組成一組,有多少不同結果(組合問題)。
③有放回地抽m個球,排成一排,有多少不同結果(可重排列問題)。
④有放回地抽m個球,組成一組,有多少不同結果(可重組合問題)。
(2)分房(占位)問題:m個人分到n個房間去住(m ①房間認為是不同的,每個房間只住一個人,有多少不同結果(排列問題)。 ②房間認為是相同的,每個房間只住一個人,有多少不同結果(組合問題)。 ③房間認為是不同的,每個房間住的人數不限,有多少不同結果(可重排列問題)。 ④房間認為是相同的,每個房間住的人數不限,有多少不同結果(可重組合問題)。 (3)利用排列組合求概率的基本思想方法。 ①合理構建樣本空間,決定是用排列思想還是用組合思想求概率。若是既能用排列思想也能用組合思想求概率,通常用排列思想求概率,因為用組合思想求概率很容易出錯。 ②復雜問題:分步計算,先選后排。 4.利用排列組合求概率的常見問題。 ①概率論中的排列問題:相鄰問題、分隔問題、循環問題、對稱問題、可重排列問題、不盡相異元素排列問題…等。 ②概率論中的組合問題:搭配問題、分班問題、分堆問題、可重組合問題等。 三、“概率理論”教學中如何分散難點 概率論中的重要理論是大數定律和中心極限定理。在概率理論教學中分散難點,就是通過概率理論的產生、建立、完善過程中所體現的數學思想方法與實例,進行分散,構造教學結構,實施教學。 在中心極限定理的教學中,我們可以通過中心極限定理的產生過程中所體現的數學思想方法,分散難點,進行教學,以加深學生對中心極限定理的理解與掌握。
人們在實踐中發現,許多隨機現象都服從正態分布,于是提出兩個問題:(1)為什么正態分布廣泛存在。(2)滿足什么條件的隨機現象服從正態分布。這兩個問題從18世紀開始,在長達兩個世紀的時間內成為概率論研究的中心,對這兩個問題研究得出的有關理論稱為中心極限定理。
通過對這兩個問題的研究得出:如果某個隨機變量,是由許多獨立隨機變量的總和組成,而每個隨機變量對于總和都不起主要作用,那么這個隨機變量就近似地服從正態分布。
因現實世界中,許多隨機現象都是由一些獨立隨機現象的總和組成,且每個隨機現象對于總和都不起主要作用,故服從正態分布的隨機現象較多。在獨立同分布的中心極限定理中,每個隨機變量都是獨立同分布,故不存在起主要作用的隨機變量,所以和式近似服從正態分布。
四、“概率教學結構的建構”教學中如何分散難點
在概率教學結構的建構教學中分散難點,一種方法就是在已知教學結構構建過程中,所體現的數學思想方法的基礎上,通過類比推廣增加建構新的教學結構,進行分散,實施教學。
對于二維隨機變量分布的教學結構的建構,就是依據一維隨機變量分布的教學結構,通過類比推廣增加的方法,進行分散,從而建構出二維隨機變量分布的教學結構。
1.一維隨機變量分布的教學結構:
(1)離散型。
①定義,②表示法,③性質,④常見分布,⑤函數分布。
(2)連續型。
①定義,②分布密度性質,③常見分布,④函數分布。
2.依據一維隨機變量分布的教學結構,通過類比推廣增加,建構二維隨機變量分布的教學結構:
通過類比與一維隨機變量分布教學結構類似的內容:
(1)離散型。
①定義,②表示法,③性質,④常見分布,⑤函數分布。
(2)連續型。
①定義,②分布密度性質,③常見分布,④函數分布。
因二維隨機變量含有二個變量,故需要推廣增加有關它們間關系的內容。在二維隨機變量分布的教學結構中需要推廣增加的內容:
(1)離散型。
⑥邊際分布,⑦獨立性,⑧條件分布。
(2)連續型。
⑤邊際分布,⑥獨立,⑦條件分布,⑧極值的分布。
總之,在概率論教學中恰當合理地運用“分散難點”的教學方法,就能實現教師輕松講、學生輕松學,就能使教學成為藝術享受,就能使學生學得更好,同時它也是反映教師教學水平的一項重要指標。
最后還應該指出的是,“分散難點”沒有固定、明確的一般方法,要具體問題,具體分析,但只要教師在備課與教學過程中,始終想到如何提高教學質量,如何使學生學得更好,那么在教學中就一定會體現“分散難點”的教學思想或創建出“分散難點”一些具體方法。
參考文獻:
[1]宋長明,張建林,江世景.案例教學法在概率統計教學中的應用[J].開封教育學院學報,2009,29(4):76-77.
[2]陳建蘭,胡曉敏.概率論與數理統計課程教學改革的研究與探討[J].教育教學論壇.2014,(20):49-50.
[3]茆詩松,程依明,濮曉龍.概率論與數理統計[M].北京:高等教育出版社,2011.
[4]盛驟,謝式千,潘承毅.概率論與數理統計[M].北京:高等教育出版社,2008.
[5]繆銓生.概率與統計[M].上海:華東師范大學出版社,2007.
[6]牛家驥.認識數學[M].吉林:吉林大學出版社,2017.

