基于CM-Q學習的自主移動機器人局部路徑規劃
張 寧,李彩虹,郭 娜,王 迪
(山東理工大學 計算機科學與技術學院, 山東 淄博 255049)
自主移動機器人的路徑規劃和避障反映的是其與環境的交互能力[1-2],它可以在給定環境執行操作時自行做出決定,這種行為已經在無人監督的任務中普及,機器人通過自主學習執行一系列動作以實現預定目標[3]。目前針對已知環境下的移動機器人避障和路徑規劃方法已經較為成熟,例如傳統的柵格法[4-5]、人工勢場法[6-7]等,或者遺傳算法、蟻群算法、Q學習等強化學習算法[8],以及較復雜的混合優化算法、基于神經網絡的深度優化算法[9]等。
針對未知環境下或者局部情景中的移動機器人路徑規劃和避障問題,由于移動機器人沒有先驗知識,對環境了解較少,無法確定所在運行環境中障礙物數量和具體位置,僅僅通過其自身攜帶的傳感器進行環境探測,感知信息并進行局部路徑規劃,效果不理想。因此,移動機器人在未知的非結構化環境下進行路徑規劃時,缺乏適應能力和自主學習能力。學者采用強化Q學習算法對移動機器人局部路徑規劃進行研究。Q學習算法由Watkins等[10]較早提出,在強化學習中應用廣泛,是不依賴于環境的先驗模型,也是一種無模型的實時學習算法[11-13]。Q學習算法的迭代過程是對環境進行試錯和搜索,多次嘗試和學習可能的狀態-動作對
目前采用Q學習算法進行局部路徑規劃,存在因先驗知識缺乏而導致學習收斂速度慢的情況,學者提出了改進的Q學習算法,如胡俊等[16]在Q算法初始化時加入對環境的先驗知識作為搜索啟發信息,提出了基于先驗知識的Q學習算法(Priori Knowledge-Q Learning),以滾動學習方法解決大規模環境下機器人視野域范圍有限,以及因Q學習的狀態空間增大而產生的維數災難等問題。這種方法在一定程度上解決了算法初始階段探索和學習的盲目性,但在局部規劃過程中有限的先驗知識只能引導機器人有目的地選擇部分路徑點,可能得不到局部最優路徑。Low等[3]利用花授粉算法(Flower Pollination Algorithm)合理地初始化Q學習算法,并運用于移動機器人路徑優化,加快了Q學習算法收斂速度,但只運用在簡單的障礙物環境中,對于復雜多障礙物環境下的路徑規劃沒有涉及。
針對上述研究的不足,本文在柵格地圖的基礎上提出了一種基于CM-Q的移動機器人局部路徑規劃算法。該算法利用Q學習算法學習最佳狀態-動作對,并引入柵格地圖中障礙物的坐標變量,利用CM算法進行坐標匹配,以解決移動機器人運行過程中的避障問題,提高移動機器人運行效率,同時規劃出局部最優或次優路徑,增加算法收斂速度。
1 柵格地圖
本文使用柵格地圖作為移動機器人路徑規劃的環境。將移動機器人的實際運行環境量化為柵格,每個柵格表示一個坐標點,并與移動機器人大小相同,起點和終點分別占據一個柵格位置,移動機器人每移動一步的步距大小為一個柵格。
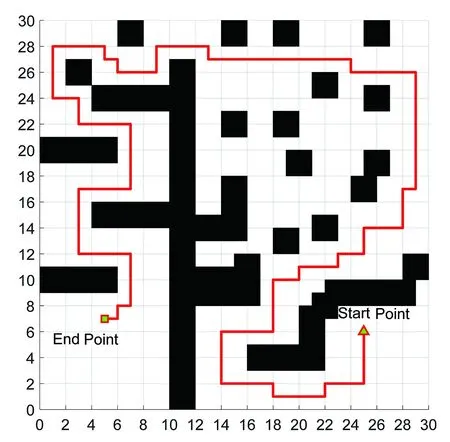
移動機器人的任務是在建立的柵格地圖中,利用給定的起點和終點,通過對環境的探測學習,尋找到一條從起點到終點、安全避開障礙物的路徑,同時使規劃的路徑最短。如圖1所建立的柵格地圖中,移動機器人通過在柵格中自由行走,學習避障,最終要規劃出一條從起點Start到終點End的最優或次優無碰撞路徑。規定柵格地圖邊界為障礙區域,移動機器人不能越界,越界視為與障礙物發生碰撞。
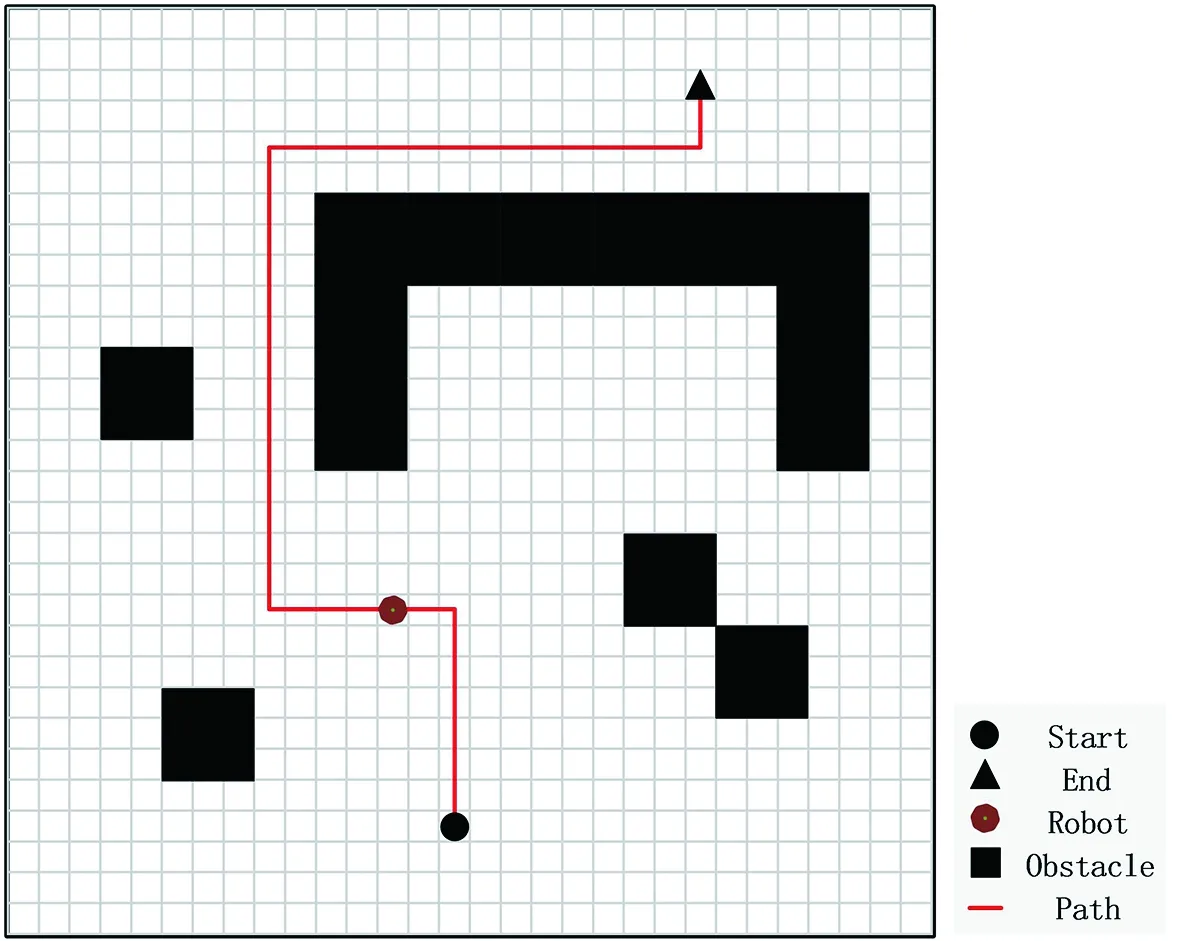
圖1 柵格地圖Fig.1 Grid map
將柵格地圖記為ΩEN,它是一個未知的有界靜態環境,它的大小為ΩEN=XLim×YLim,且XLim、YLim為大于0的整數。記ΩEN中移動機器人的起始位置和目標位置分別為Ωstart和Ωend,并且Ωstart≠Ωend,Ωstart∈ΩEN,Ωend∈ΩEN。
ΩEN中分布著有限個靜態障礙物ob1、ob2、···、obn。建立與ΩEN大小相同的Ωtable表作為柵格環境二維表,記錄所檢測到的柵格環境中的障礙物位置。Ωtable表中的行、列分別表示組成障礙物obi的各橫、縱坐標。
規定柵格環境二維表Ωtable中每個最小單位障礙物obi由9個坐標構成,每個坐標由單個障礙物obi的對角線交點的橫縱坐標及其相應形式表示,記為Ob_bn。組成obi的各坐標為Ob_os,表示為
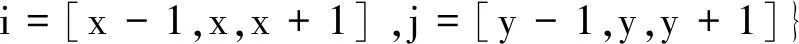
(1)
單個方形障礙物坐標位置示意如圖2所示。
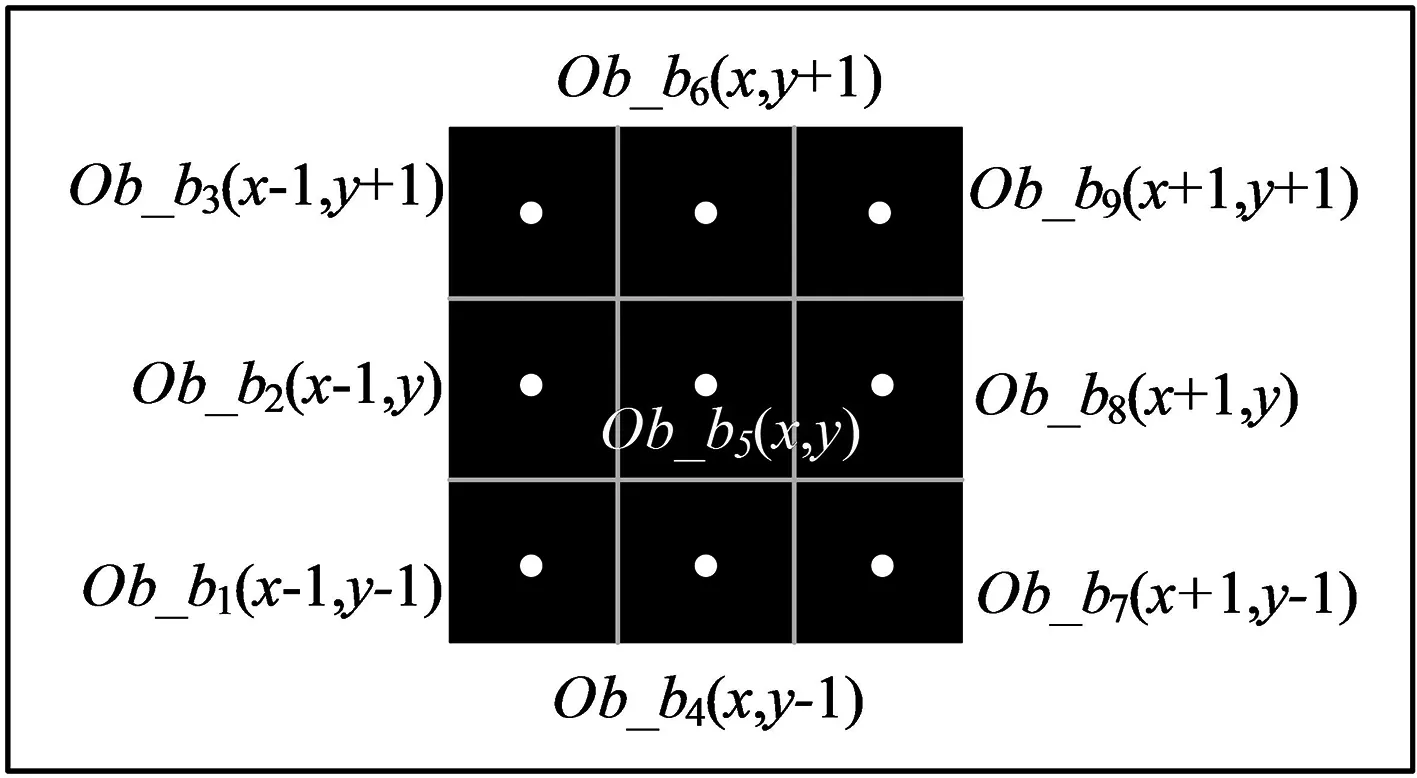
圖2 單個方形障礙物各頂點坐標示意Fig.2 The coordinates of each vertex of a single square obstacle
所有單個障礙物坐標集Ob_os組成全部障礙物坐標集,用Ob_pos表示。在ΩEN中標記障礙物所在位置的坐標為
(2)
2 CM-Q學習算法
本文使用Q學習算法來學習最佳狀態-動作對,利用坐標匹配的CM算法進行避障,以完成移動機器人的局部路徑規劃任務。
2.1 狀態和動作描述
移動機器人從起點出發,不斷探索未知環境,每次成功到達終點時所走過的路徑由ΩEN中對應的坐標點聯結成的軌跡表示。其中,移動機器人在其所在運行環境中的每個坐標點表示一個狀態,記為st,坐標為Ωst。根據柵格地圖模型的維數,共有XLim×YLim個狀態,所有狀態組成的狀態集S為
S={st|st=Ωst(i,j),i∈XLim,j∈YLim}
(3)
每個狀態下,移動機器人可以執行的動作記為ai。動作可根據當前所處的狀態隨機進行選擇,這里規定移動機器人只能執行上、下、左、右4個動作,每個動作每次移動1個坐標(或1個柵格)位置,動作集A表示為A={ai,i=1,2,3,4}。
當前動作的選擇影響下一個狀態的表示,這里規定狀態和動作之間以坐標進行轉換。移動機器人執行4個動作時所對應狀態的變化見表1。
表1 狀態-動作關系表
Tab.1 The relationship between state and action

集合對應關系狀態集S st+[0,1]st+[-1,0]st+[1,0]st+[0,-1]動作集Aa1(上)a2(左)a3(右)a4(下)
2.2 Q矩陣建立
Q矩陣是用來存儲最佳狀態-動作對Q值的有限二維表,它的大小由狀態和動作決定,狀態的大小為XLim×YLim,動作為4,所以Q矩陣的大小為XLim×YLim行、4列。Q矩陣表示為
QXLim×YLim×4=
(4)
Q矩陣中每個Q值為移動機器人學習過程中在st狀態下,采取動作ai到達下一個狀態時,所獲得的最大獎勵期望值。當Q矩陣中的每個Q值的變化率△Q(st,ai)小于給定的精確度時,Q矩陣收斂,每個Q值都趨于穩定。
由于每次從起點到終點的最優或次優路徑可能不止一條,所以每當學習結束時所得到的最佳狀態動作對
2.3 回報函數設計
回報函數是用來評價移動機器人避開障礙物并趨向目標行為的判斷標準,最終使移動機器人學習規劃的路徑安全、最短。
將回報函數Rew(r)設計成獎勵和懲罰兩類。令r為獎懲情況種類,用來判斷移動機器人當前所處狀態,根據狀態給予獎懲。r1表示沒有碰到障礙物,獎勵為0;r2表示到達終點,獎勵100;r3表示碰撞障礙物,懲罰100。回報函數表示為
(5)
2.4 CM避障設計
移動機器人在移動的過程中要進行避障,采用CM避障設計方法,即移動機器人每執行一次動作后的坐標與柵格地圖中障礙物所在位置坐標進行匹配,快速判斷移動機器人當前運行方向是否存在障礙物,提高其路徑搜索效率和避障能力。CM避障方法分為障礙物避障和邊界避障兩部分。
2.4.1 障礙物避障
根據移動機器人局部避障規則,建立圖3所示的局部避障模型示意圖。
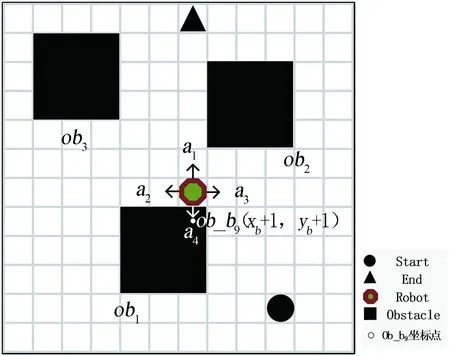
圖3 移動機器人局部避障模型Fig.3 Local obstacle avoidance model of mobile robot
設當前移動機器人的坐標為R(xr,yr),令障礙物ob1中心點的坐標為Ob_b5(xb,yb),根據式(1)和圖2所示,障礙物ob1右上角Ob_b9坐標等于(xb+1,yb+1)。移動機器人在柵格環境中進行探索學習過程中,執行動作a4后,移動機器人會與障礙物ob1的右上角發生碰撞,此時移動機器人的坐標為R(xr,yr)+(0,-1)=R(xr,yr-1),將R與組成障礙物ob1的各個坐標進行匹配,找到碰撞點的坐標,即R(xr,yr-1)=Ob_b9(xb+1,yb+1),如果xr=xb+1且yr-1=yb+1,說明移動機器人在學習過程中執行動作a4后,碰撞了障礙物。
根據回報函數獎懲規則,發生碰撞對應的表示關系為r3,則Rew(r3)=-100,移動機器人在學習過程中受到懲罰,當下一次遇到類似情況時,移動機器人將不會執行動作a4而執行其他動作。
2.4.2 邊界避障
移動機器人在柵格環境邊緣的行為情況分為兩類8種,即左、上、下、右4種側邊界動作情形和左上、左下、右下、右上4種角邊界動作情形。移動機器人在側邊界和角邊界能夠執行的動作分別如圖4(a)和圖4(b)所示。
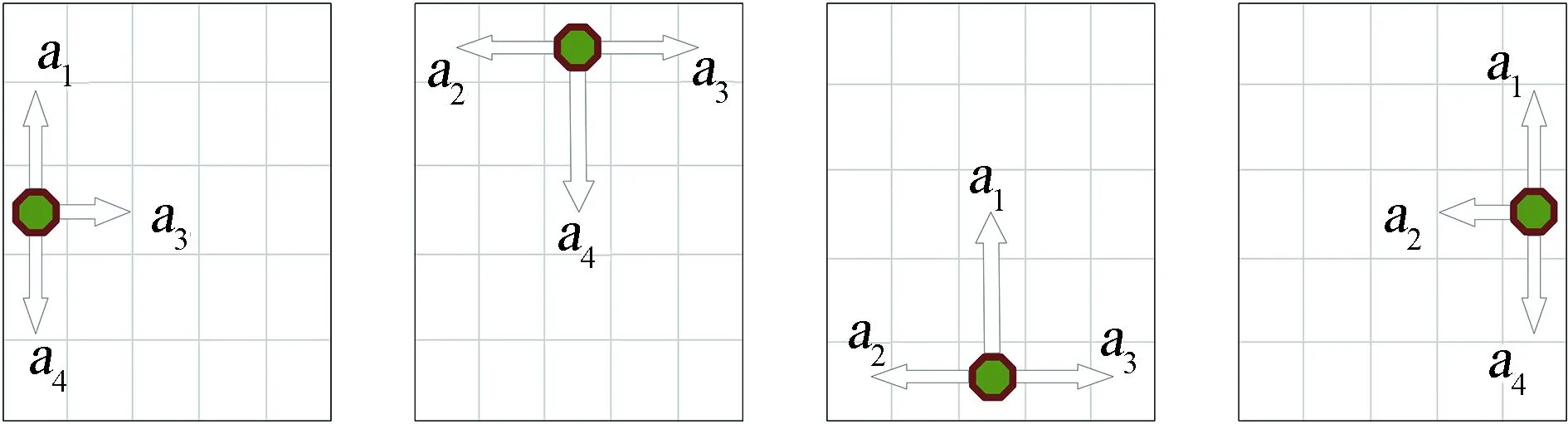
(a)側邊界動作示意
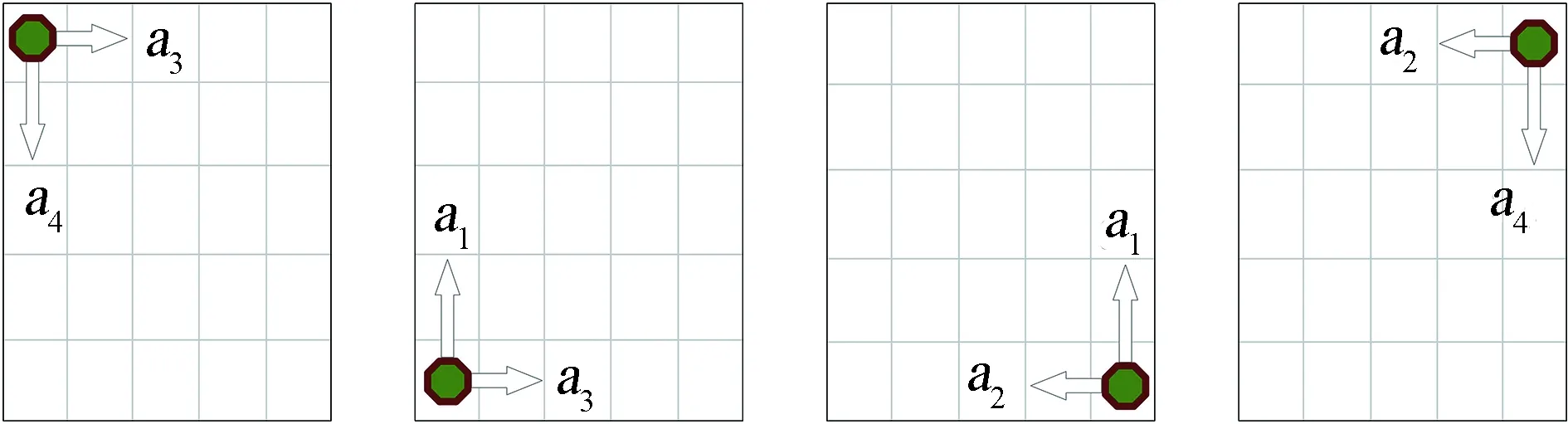
(b)角邊界動作示意圖4 柵格側邊界和角邊界動作執行示意圖Fig.4 Schematic motion execution diagram of grid side boundary and corner boundary
將底邊界、左邊界、上邊界、右邊界坐標分別表示為(x,0)、(0,y)、(x,YLim)、(XLim,y),移動機器人按照CM算法進行避障時,如果其坐標R(xr,yr)等于任意一個邊界坐標,則與邊界發生碰撞,根據獎懲規則,Rew(r3)=-100,移動機器人受到懲罰,通過不斷學習,最終移動機器人不再碰撞邊界。
2.5 基于柵格地圖的CM-Q算法
基于所建立的柵格地圖,運用CM-Q學習避障和路徑規劃的步驟如下:
(1)清空二維環境表EN和障礙物坐標集Ob_pos,給定移動機器人起點Ωstart和終點Ωend,給定障礙物obi。
建立short_best線性表,存儲從起點到終點的歷史最佳狀態-動作對
初始化移動機器人即時回報Rew0=0,目標點回報值Rewend=100,學習次數初值0,最大學習次數Nmax。
用貪婪策略確定學習率α的公式為
(6)
式中:fix()為取整函數;通常0≤α<1。當給定初始α0值、LearnN、Nmax時,α值可以決定Q值更新速率。
(2)初始化歷史最短路徑長度shortbest_size=Nmax,迭代計數器初值count=0,清空當前最短路徑記錄表short_list。
(3)移動機器人對所處狀態進行判斷,對于?st∈S,若Ωst∈Ob_pos,則發生碰撞,利用CM-Q算法進行避障,令st+1=st并轉到第(4)步;否則根據式(7)選擇當前狀態st下Q值最大的動作ai執行。
(7)
執行動作ai后,移動機器人轉為狀態st+1,count=count+1,此時若Ωst=Ωend,則轉至第(5)步,否則轉至第(7)步。
(4)計算當前環境回報值,用式(5)對移動機器人當前狀態-動作執行情況給予獎懲,求出回報函數的值Rew(r)。若移動機器人受到獎賞,則轉到第(6)步;若移動機器人受到懲罰,則退回上一狀態并轉至第(3)步。
(5)當前狀態為目標狀態,記下當前迭代計數器count的值、歷史最短路徑short_best及其長度shortbest_size,以及當前最短路徑short_list,并轉至第(2)步。
(6)當前狀態下的強化Q值按式(8)進行更新:
(8)
式中γ為折扣因子,0≤γ<1,通常選擇較大的γ使移動機器人獲得未來回報的機會更大。在極端情況,當γ=0時機器人只考慮行動的當前回報;當γ接近1時,未來的回報在采取最優行動時變得更為重要。
記錄當前狀態的最短路徑short_list并轉至第(3)步。
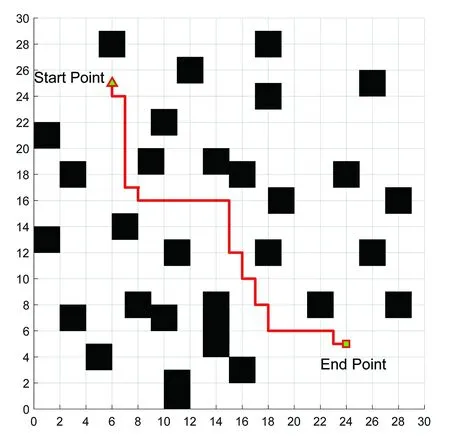
(7)若LearnN 實驗環境為windows7,Intel(R)Core(TM)i5-2400CPU3.1GHz,6GB內存,仿真工具為matlabR2016a。在仿真環境下對本文所提CM-Q算法進行測試,驗證算法有效性,并將結果與文獻[3,17]的進行冗余度比較。 實驗均在大小為30×30的柵格環境下進行,運行環境中的起點、終點和障礙物隨機設置。進行多次實驗后,根據式(4)和式(8),Q值變化率△Q(st,ai)小于給定精確度時,Q矩陣收斂。Q值中包含了式(5)的趨向于最優或次優路徑的評價指標Rew(r),則Q矩陣收斂后獲得的路徑即為最優或次優路徑。 未知簡單障礙物環境下的移動機器人學習之后的路徑規劃仿真結果如圖5所示。圖5中設置的起點為(6,25),終點為(24,5)。移動機器人各次學習情況見表2。 圖5 未知簡單環境下路徑規劃Fig.5 Path planning under unknown simple environment 表2 簡單環境下CM-Q算法學習測試 實驗次數平均學習次數平均路徑長度/cm平均用時/s106624638.28205904436.94306904039.88406803837.25506333835.12606323834.97706333835.10806333835.08 在未知簡單障礙物柵格環境中加入類似迷宮的障礙物,組成混合復雜障礙物環境,路徑規劃結果如圖6所示。起點和終點分別設置為(25,6)、(5,7),CM-Q算法所用參數設置不變。移動機器人各次學習情況見表3。算法收斂速度與迭代學習次數關系如圖7所示。移動機器人到達目標時的平均路徑長度與迭代學習次數的關系如圖8所示。 圖6 混合復雜障礙物環境下規劃路徑Fig.6 Path planning under complex and mixed environment 表3 混合環境下CM-Q算法學習測試 實驗次數平均學習次數平均路徑長度/cm平均用時/s101 874147113.74201 915132111.93301 987119118.62401 940111110.75502 000108105.36601 999108105.30702 001108105.39802 000108105.33 圖7 算法收斂速度與迭代學習次數關系Fig.7 Relationship between algorithm convergence speed and iterative learning times 圖8 平均路徑長度與迭代學習次數關系Fig.8 Relationship between average path length and iterative learning times 由表2和表3可知,在相同實驗設定下進行了不同次數的實驗,隨著實驗次數的增加,平均路徑長度減小,說明還有少數狀態沒有學習到。當進行了50次實驗后,平均學習次數基本穩定,此時從起點到終點的所有狀態都學習完畢,Q矩陣收斂,如果再進行更多次實驗,平均路徑長度不再變化。 圖7中,算法收斂速度(cm/s)=迭代路徑長度(cm)/間隔時間(s),其中迭代路徑長度為迭代過程中每次找到的一條從起點到終點的可行路徑長度,間隔時間為后一次找到可行路徑用時與前一次找到可行路徑用時之差。由圖7可知,CM-Q算法收斂速度隨著迭代次數增加而增大,開始時由于移動機器人需要大量探索環境,所以230次前Q矩陣變化不大,算法基本不收斂,后期算法收斂速度逐漸加快。 由圖8可知,由于前期算法收斂較慢,所以移動機器人到達終點所走路徑較長;后期算法收斂后,Q矩陣中各Q值基本穩定,移動機器人通過查找Q值表,選擇最佳動作執行,很快到達了終點。 在未知連續障礙物環境下利用CM-Q算法進行了多次路徑規劃冗余度測試,并與文獻中的算法進行冗余度對比。實驗中起點和終點分別為(12,1)和(22,23),所規劃路徑如圖9所示。 圖9(a)展示了移動機器人利用CM-Q算法進行路徑規劃仿真實驗的結果。圖9(b)顯示了移動機器人在相同的環境下利用文獻[3]中的算法進行路徑規劃的仿真實驗結果。圖9(c)顯示的是文獻[17]中利用模糊控制策略和狀態記憶規則進行路徑規劃的仿真實驗結果。 (a)CM-Q算法路徑規劃 (b)文獻[3]路徑規劃 (c)文獻[17]路徑規劃圖9 未知連續障礙物環境下的路徑規劃Fig.9 Path planning under unknown continuous obstacles environment 本文以路徑長度和移動機器人轉彎次數作為評判所規劃路徑冗余程度的標準,結果見表4。 表4 路徑長度和轉彎次數 算法平均路徑長度/cm轉彎次數/次CM-Q7211文獻[3]7413 由表4可知,利用CM-Q算法規劃路徑的長度和移動機器人的轉彎次數均比文獻[3]中的小。由圖9(c)可知,文獻[17]路徑較平滑,但是路徑冗余度明顯比CM-Q算法和文獻[3]算法的路徑長。基于以上實驗結果可知,利用CM-Q算法進行移動機器人路徑規劃的效果較好,規劃出的無碰路徑冗余度較低。 針對移動機器人在未知、復雜環境下避障問題和路徑規劃過程中出現的路徑冗余問題,本文提出了CM-Q學習算法。該算法基于移動機器人行走過程中當前位置的坐標與最鄰近障礙物的坐標是否相等的判斷,對移動機器人當前狀態進行評價和獎懲,并在多障礙物的未知環境下進行最短路徑學習。通過避障學習和獎懲措施,提高了最佳狀態-動作對的搜索速度和環境適應能力,同時在基于柵格地圖的復雜障礙物環境中成功地規劃出一條最優或次優路徑。仿真實驗結果表明,該算法簡單、有效可行,不受U型障礙物的死鎖和震蕩干擾。此算法有待于從時效性和動態障礙物實時避障方面進行改進。3 仿真實驗及結果分析
3.1 CM-Q算法有效性驗證
Tab.2 Test result of CM-Q learning algorithm under simple environment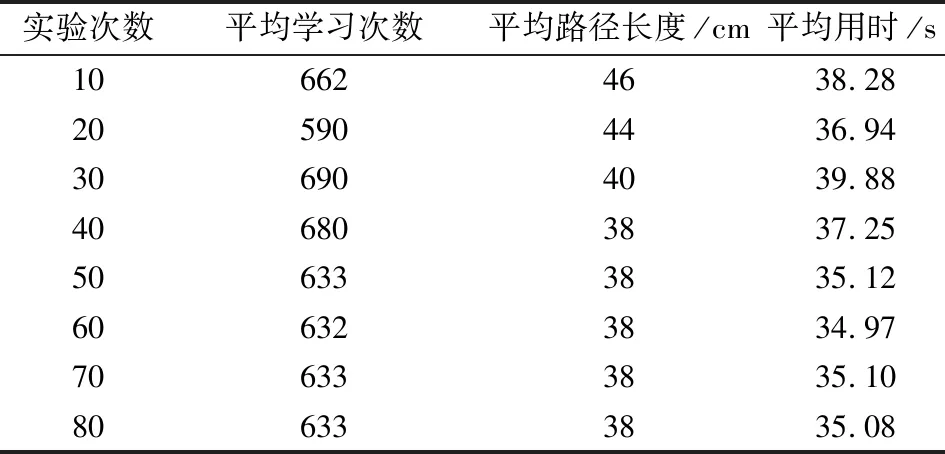
Tab.3 Test result of CM-Q learning algorithm under complex and mixed environments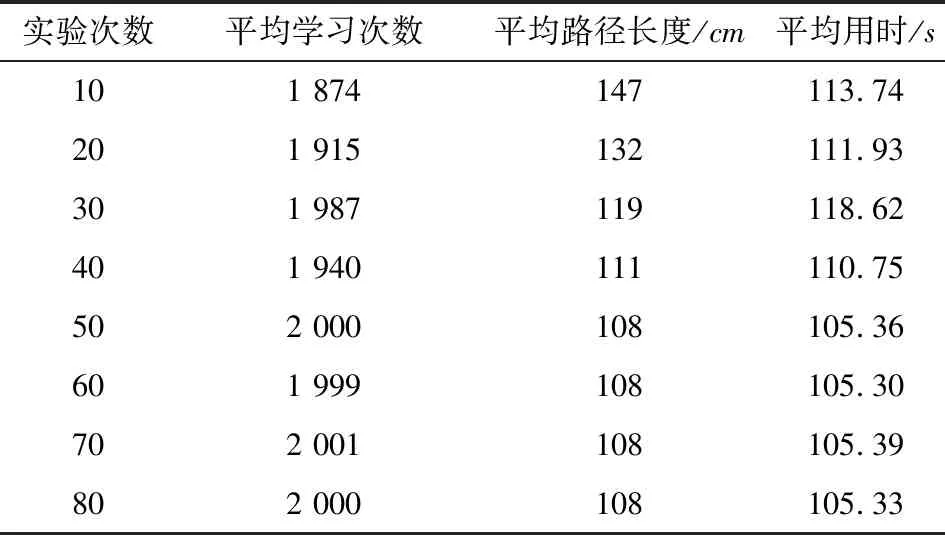
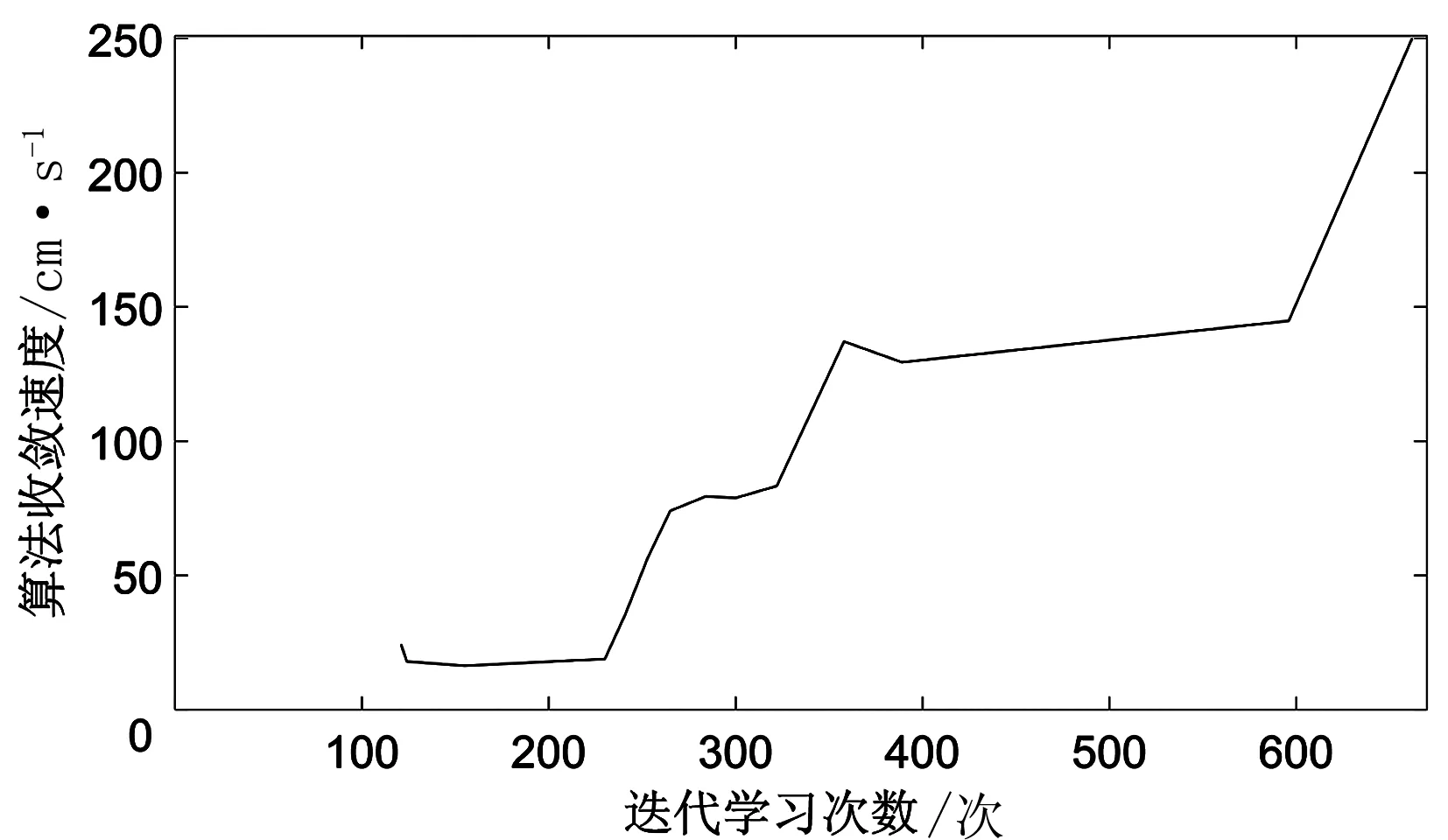
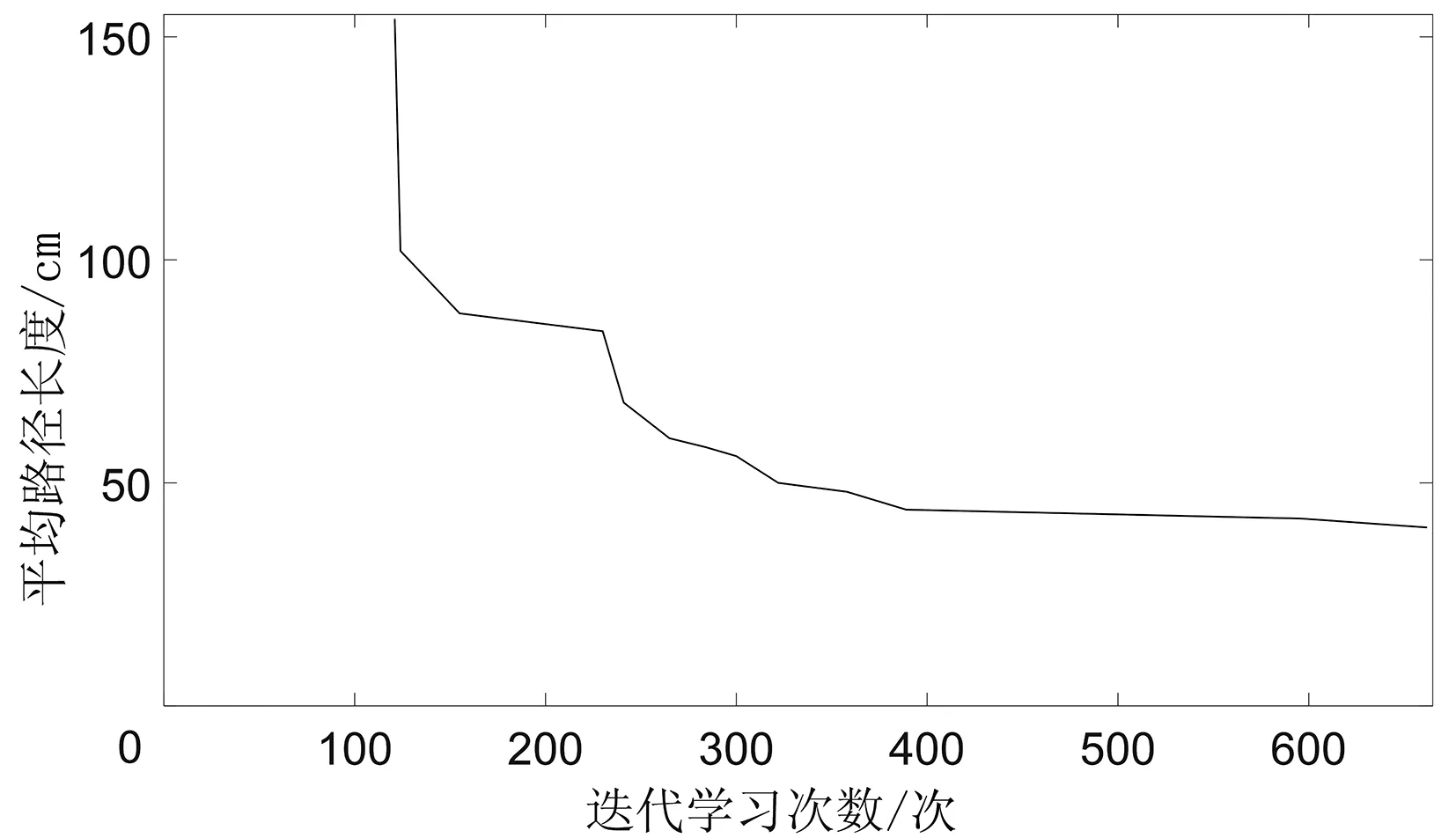
3.2 路徑規劃冗余度測試
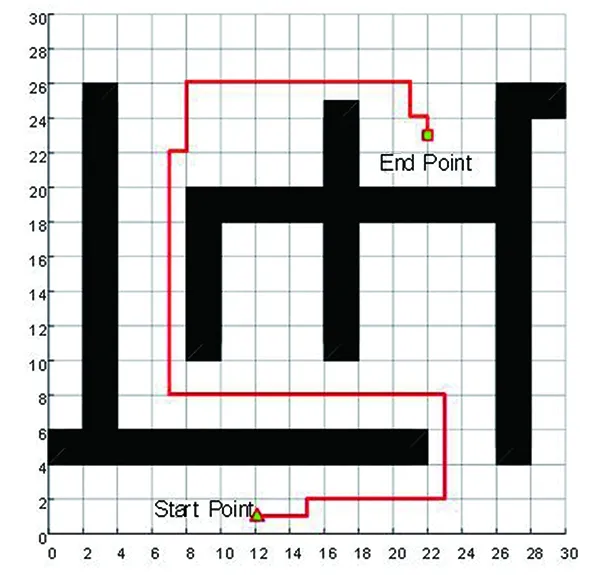
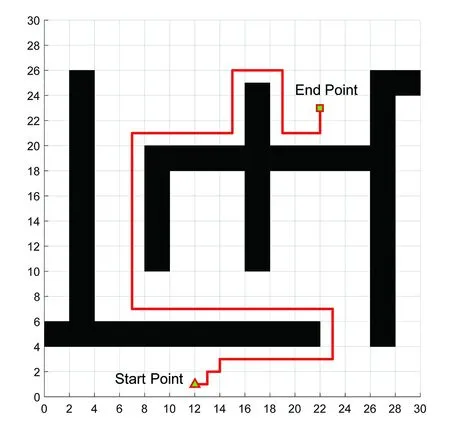
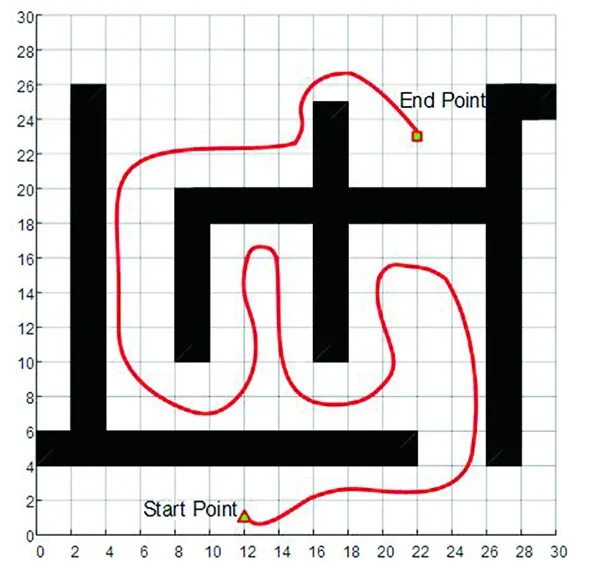
Tab.4 The path length and the turning times
4 結束語

