滲透模型思想 發展結構性思維
四川省成都市武侯實驗中學附屬小學 唐 斌 付興容
所謂“高階思維”,是指發生在較高認知水平層次上的心智活動或認知能力;高階思維具有發散性、結構性、主動性、批判性等特質。思維的“結構性”是高階思維的一個重要方面,主要是指有序的、系統的立體化思維方式,具有系統性、遷移性、本質性、創造性等特點。結構性思維,能使方法簡潔、分析深邃、決策高效,問題解決能力強。數學教學中,以結構化教學統整數學結構化知識,培養學生結構性思維。教學中滲透模型思想,以“建模”“用模”“變模”“超模”為具體路徑,發展學生思維系統性、遷移性、本質性、創造性,培養學生 結構性思維,進而發展學生高階思維能力。
一、構建數學模型,從“無形到有形”,優化認知結構,發展系統性思維
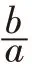
例如:暑假到了,瑞瑞一家三口自駕從成都到西昌旅游,距離約是450 千米。他們早上9:30 從家出發,上午11:30 到達名山服務區,汽車行駛了150 千米。休息半小時后按原速繼續行駛,中午吃飯花了一小時,下午6:00 能到達西昌嗎?自駕游已成為現在家庭旅游的交通方式之一,學生在生活情境中會經常遇到此類問題,解決生活中的實際問題更能激發學生學習的內驅力,調動學習的積極性、主動性。學生根據問題及信息梳理問題結構:求結束時間,必須先求經過時間;算經過時間需要路程與速度;但由于題中沒有明確告知汽車行駛的速度,因此需要借助“早上9:30從家出發”“上午11:30 到達名山服務區”這兩條信息先求出經過時間,再用已學習的“路程÷時間=速度”運算模型,算出汽車行駛的速度。接著算出剩下路程所用時間,再算出總共所花的經過時間,最后算出結束時間,與下午6:00 進行比較。學生在解決此問題過程中,構建了新的認知體系,抓速度不變,構建“路程÷時間=速度”關系模型,系統化思考“余下路程所用時間”的新問題。
二、巧用數學模型,由點及面,深化模型內涵,發展遷移性思維
結構化思維,不僅體現數學模型的系統構建,而且表現在模型的靈活運用上,運用已有的模型解決新問題,深化對模型內涵的理解,發展遷移性思維。模型應用,串式思考,縱向延伸,深入分析問題的本質,如倒數在分數除法算法中的應用,進一步探究“倒數”概念的作用,深入體會“倒數”的本質意義;橫向聯系,網狀思考,建立不同問題間的聯系,立體挖掘模型意義,如分數與整數、小數、百分數、比等之間的必然聯系。從“縱”“橫”角度,從點到面,將知識結構內化為思維結構,提高模型的應用能力。
“以一定的邏輯順序整合、內化知識結構,是結構化思維的真諦所在。”例如,《小兔請客》(北師大版一年級下冊),學生觀察情境圖收集數學信息“左邊擺了2 盤果子,右邊擺了3 盤果子,每盤有10 個果子”,提出數學問題:“一共有多少個果子呢?”這是學生第一次接觸超過20 的加法計算。用小棒代替果子,借助學具進行操作,讓學生擺一擺,說一說有多少根小棒。部分學生借助小棒,將“一盤10個”與“一捆10 根”對應,進行“10個10 個地數”,體現了數數模型的運用與遷移:“1 捆有1 個10,左邊的2捆就有2 個10,右邊的3 捆就有3 個10,合起來就有5 個10,也就是50。”數數模型進一步發展到加法計算模型:“因為2+3=5,所以2 個10+3 個10=5個10 也就是50。”借助數的意義“2個10 加3 個10 等于5 個10”,運用“10以內加法”模型,拓展到“10 以上加法”模型,縱向聯系,進一步體現了加法計算法則的內涵“相同的計數單位相加”。由整數加減法,到小數、分數加減法,橫向勾連,都是應用“相同的計數單位相加減”模型進行計算。學生掌握了計算模型,有助于培養學生舊知識解決新問題的思維遷移能力。
學習整十數的加法計算,就是學生學習加法運算的意義,及經歷整數、小數、分數加減法計算算理建模的過程。由一個知識點“2 個10 加3 個10”延伸至一類知識“小數、分數的加減計算”,凸顯出數學知識結構化,便于學生抽象出數學模型——相同的計數單位才能相加減,這便是將一個問題的解決拓展為一類問題的解決,讓學生對數學本質有了全面、深刻的理解,培養學生高階思維能力。
三、變換數學模型,由表及里,拓展模型外延,發展本質性思維
遵循知識間的邏輯關系,把握知識點在知識結構鏈中的具體位置,以“刨根問底”的態度,以問題串形式,由表及里,追尋知識的本質,進而發展本質性思維。立體多向思考,突破模型化的思維定式,破解“套模”,變換模型的不同式樣,建立模型間關系;從不同角度拓展模型外延,進一步理解數學模型的本質。
在建立牢固的知識結構的同時,建立良好的思維結構。如“雞兔同籠”問題,學生學會列表法后,再探討多種方法,拓展問題解決模型,進一步提出問題,以“問”促進思考,優化思維結構。如“還有哪些方法?你覺得哪種方法更簡單?這些方法分別適用于哪些情況?……”學生嘗試其他方法如極端假設法、任意假設法、除減法、盈虧法、比例分配法、布列方程法等,在多種方法的對比中,“以一帶多”,明白此類問題的內涵。改變模型條件,擴大模型外延,運用聯系的思想,由表及里,認識模型本質。引導學生發現“雞兔同籠”問題的多種表現形式,明確問題的本質都是“猜想”“轉化”等數學思想的體現,抓住了本質,方可舉一反三。如三輪與四輪車并存、運貨運費中賠償問題、晴天雨天摘果子問題等,都可以用“同籠”方法解決。由“雞兔同籠”問題基本模型“已知雞兔頭之和與足之和,求雞兔各有多少只”,到變換條件“已知雞兔頭之和與足之差”“已知雞兔頭之差與足之和”“已知雞兔頭倍數與足之差”“已知雞兔頭倍數與足之和”“已知雞兔頭之和與足倍數”等,求“雞兔各有多少只”;如此拓展了“雞兔同籠”的問題解決基本模型,進一步鞏固“假設”“轉化”的數學思想,靈活運用列表法或方程法解決問題,在建立知識結構的同時,優化思維結構,發展解決問題的高階思維 能力。
四、超越數學模型,從有形到無形,深化數學思想,發展創造性思維
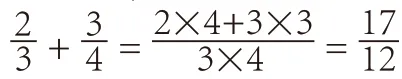
再如,一個長方體,如果長增加2 厘米,則體積增加80 立方厘米;如果寬增加3 厘米,則體積增加150 立方厘米,如果高增加4 厘米,則體積增加320 立方厘米。那么原來長方體的表面積是( )平方厘米。學生發現以“長方體的表面積=(長×寬+長×高+寬×高)×2”計算模型無法解決此問題,需要運用原始模型——表面積概念“長方體各面面積之和”,部分學生借助畫圖,突破原有的認知結構,借助轉化的數學思想,超越與突破了基本計算模型,找到新的計算方法。根據題目信息間的關系,重新建立“體積÷長=左(右)面面積”“體積÷寬=前(后)面面積” “體積÷高=上(下)面面積”“(左面積+前面積+上面積)×2=表面積”計算結構。雖建立了長方體表面積公式的數學模型,但由于此問題比較抽象,學生的空間觀念不強,因此僅靠讀題無法找到數學信息與問題之間的聯系。畫圖中運用轉化思想把抽象的數學問題用具體、形象、直觀的圖示表示出來,引領學生找到解決問題的關鍵,讓學生感受到“柳暗花明又一村”。運用轉化思想不僅提高了學生解決問題的能力,提高了學生靈活運用數學模型舉一反三的能力,培養了他們的創造性思維,促進高階思維能力發展。
數學課堂教學滲透模型思想,培養學生從混亂中找到順序,從零散中找到關系,從發散中找到核心,從現象中抽象出本質,從變化中學會創造的思維能力,促進學生結構性思維能力的提升,從而發展學生高階思維能力。方法是路徑,思想是靈魂。沒有思想的方法僅是呆板工具;蘊含思想的方法,才有強大生命力!

