板翅式換熱器封頭應變試驗及塑性壓力研究*

張 旭，鄒先平

（1.遵義師范學院 工學院，貴州 遵義 563002；2.珠海格力電器股份有限公司，廣東 珠海 519070）

0 引 言

板翅式換熱器在石化、空分、核工業領域應用廣泛[1]，其正交接管封頭作為帶接管壓力容器的一種，封頭強度設計及可靠性問題一直是研究的重點。根據美國機械工程師協會[2]（American Society of Engineers，ASME）頒發的鍋爐及壓力容器規范要求可知：設計許用壓力可根據壓力容器極限壓力取1.5倍安全系數所得。因此，如何確定極限壓力對工程的設計顯得十分關鍵。

理論極限壓力定義為極限狀態下的臨界壓力，其微小增量引起結構形變量的無限增大，這一定義的前提是基于理想塑性材料模型和小變形假設，但實際結構難以忽略真實材料的應變硬化和幾何強化影響。近年來，確定真實材料結構的塑性壓力[3]采用什么塑性準則成為了理論研究的核心。

塑性準則可分類為斜率準則和曲率準則。斜率代表曲線上某點切線的傾斜程度，基于斜率準則的判據是以結構載荷-應變曲線的斜率切線為指標。ASME提出了兩倍彈性斜率準則，是DRUCKER等三倍彈性斜率準則的保守提法，定義塑性壓力為危險節點的壓力-應變曲線與兩倍彈性斜率線之交點所對應的壓力值，該準則所確定的塑性壓力值偏保守且受人為因素影響較大，缺乏客觀性[4]；SAVE[5]提出了切線交點準則，定義了塑性壓力為危險節點的壓力-應變曲線上彈性部分和塑性部分的斜率切線交點對應的壓力值，該準則所確定的塑性壓力值分散性較小，唯一不足的是斜率切線的交點不在壓力-應變曲線上。

曲率代表曲線上某點的彎曲程度，基于曲率準則的判斷是以結構屈服塑性段的曲率為指標的。章為民[6]提出了ZC準則，定義塑性壓力為危險節點的壓力-應變曲線上塑性段零曲率點對應的載荷；MACKENZIE[7]提出的PWC準則以壓力-塑性功曲線塑性段曲率為0或趨近于零點對應的壓力值為塑性壓力，克服了Gerdeen準則難以應用的困難，但曲率趨近于零點對應的壓力值取舍具有主觀性[8]；CAMILLERI[9]提出了RPWC準則，以比率塑性功-壓力曲線的最大曲率點對應的壓力值為塑性壓力，塑性段最大曲率點對應的塑性壓力具有客觀唯一性。

本文研究板翅式換熱器正交接管封頭在ZC準則、PWC準則、RPWC準則下的塑性壓力計算方法，并利用正交接管封頭應變試驗中的應變檢測結果對有限元模型進行對比修正；研究塑性壓力與尺寸參數的影響關系，并給出板翅式換熱器正交接管封頭塑性壓力計算公式。

1 有限元建模及試驗研究

1.1 封頭非線性有限元分析模型

板翅式換熱器正交接管封頭結構如圖1所示。

圖1 板翅式換熱器正交接管封頭結構圖

圖1中，封頭筒體長度L=1 400 mm，接管高度H=180 mm，筒體壁厚T=16 mm，接管與筒體的壁厚比itT=t/T=1，筒體的徑厚比iDT=D/T=20，接管開孔率idD=d/D=0.6；

封頭和接管采用鋁合金材料5052-0（GB/T6893-200），材料的主要性能參數如下：彈性模量E=70 GPa，泊松比ν=0.33，屈服極限σy=109.48 MPa，塑性模量Epl=360.54 MPa，強度極限σb=250.30 MPa。

筆者在封頭筒體和接管壁面施加內壓載荷，封頭筒體底座施加固定約束。非線性有限元分析采用雙線性隨動強化模型和小變形理論，用于計算應變硬化條件下的封頭塑性壓力。

筆者建立的正交接管封頭網格細分圖如圖2所示。

圖2 正交接管封頭網格細分圖

1.2 封頭應變試驗研究

為了校準封頭有限元分析模型，需要獲取同一條件下封頭試驗與有限元分析的應力結果，并進行對比。

封頭水壓試驗采用電阻應變測量法，測試封頭在內壓增量載荷作用下的彈性應力分布情況。在封頭所在的對稱平面交線上進行應變布點，其中，靠近封頭-接管相貫線的區域全部布置BX120-3CA型三花應變片，遠離相貫線的區域采用BX120-3BA型直角應變片，應變片阻值為119.9±0.2 Ω，靈敏度系數為2.08±1%。

所建立的封頭應變測試試驗布點如圖3所示。

圖3 封頭應變測試試驗布點圖

2 曲率準則塑性壓力計算方法

確定ZC準則塑性壓力時，筆者選用封頭模型等效應力最大節點所在位置的應變作為變形參數，以該節點的壓力-應變曲線零曲率點對應的壓力值為封頭的塑性壓力。

在確定PWC準則和RPWC準則塑性壓力時，筆者采用文獻[10]中的塑性功和彈性功公式，通過ANSYS APDL語言編譯，獲得封頭模型所有單元的塑性功和彈性功總和。

筆者采用CAD建模軟件Pro/E的樣條曲線創建功能及曲率分析功能，得到各曲率準則下的精確塑性壓力值。

上述3種曲率準則確定過程及結果皆無主觀因素參與，判定方法簡便客觀。

3 塑性壓力與封頭尺寸參數關系研究

在給定封頭筒體長度L、筒體壁厚T、接管高度H的條件下，封頭建模參數可由封頭筒體與接管壁厚比itT、封頭筒體徑厚比iDT、接管開孔率idD3個無量綱參數唯一確定[11]。

為了探究3個無量綱參數對封頭塑性壓力的影響，筆者在同一材料模型條件下，進行如下序列的封頭模型計算：

開孔率idD參數序列為{0.2，0.4，0.6，0.8，0.9}；筒體徑厚比iDT參數序列為{10，15，20，25，30}；壁厚比itT參數序列為{0.4，0.8，1.2，1.6，2.0}。

4 研究結果

4.1 有限元分析與試驗測試結果

由于電阻應變計的測量量程范圍有限，要保持測試數據在量程范圍內，即應變計在彈性變形范圍內，應變測試數據才有效。

根據文獻[12]中對于復雜應變測試數據的處理方法，換算各測點的應力，方便了各測點位置的有限元分析與試驗應力結果的對比。

在8.40 MPa水壓作用下，筆者根據封頭筒體與豎直對稱平面交線上的各測點位置，實測應力及根據有限元計算應力所繪制的封頭筒體彈性應力分布，如圖4所示。

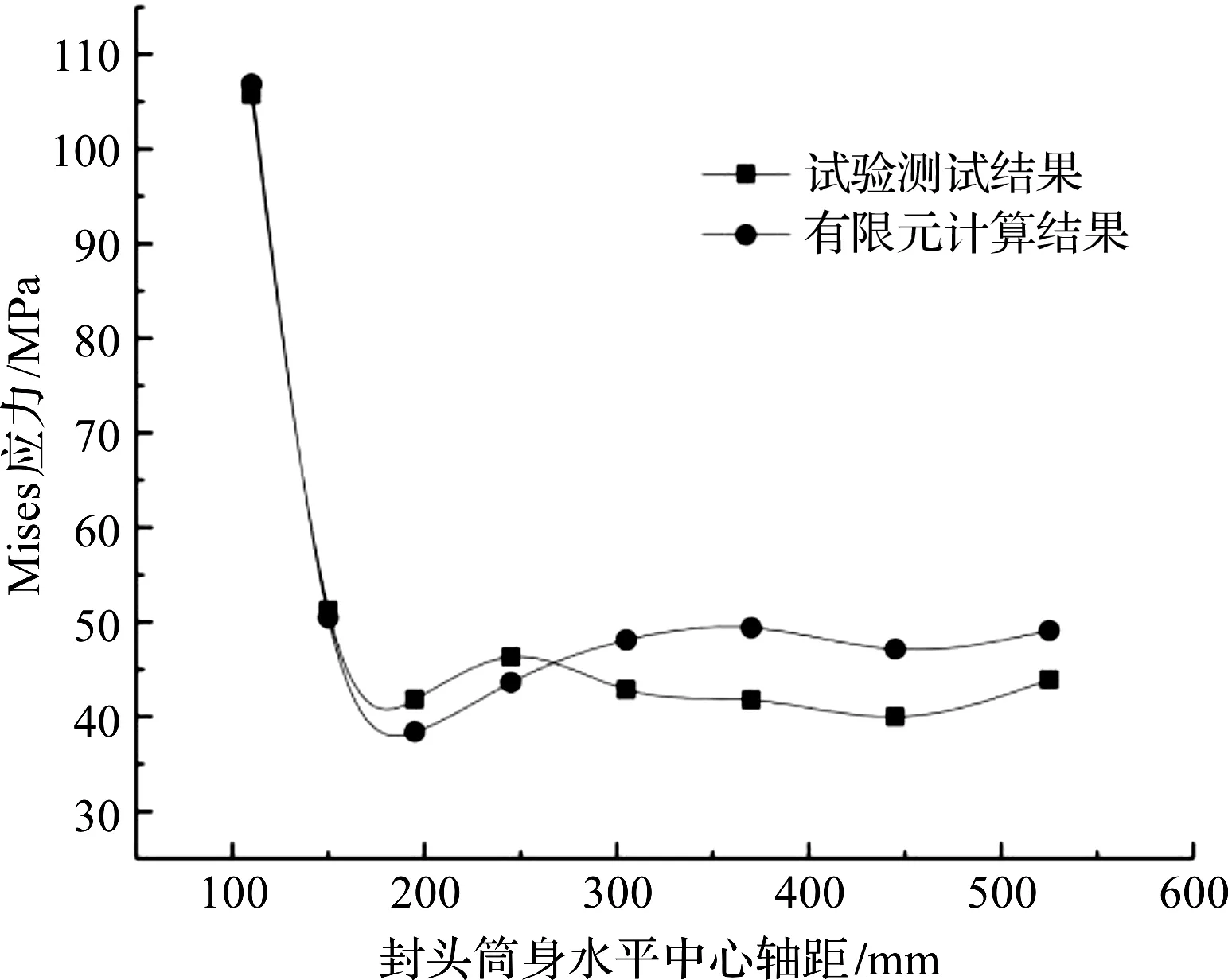
圖4 封頭筒身彈性應力分布

由圖4可知：隨著封頭筒體與豎直對稱平面交線上的各測點位置與接管之間距離的增大，實測應力數據變化趨勢與有限元計算所得結果一致；應變試驗驗證了封頭有限元建模方法的準確性；在此基礎上做曲率準則塑性壓力的研究具有準確指導性。

4.2 曲率準則塑性壓力計算結果

RPWC準則判定條件下的封頭塑性功比率-壓力載荷曲線如圖5所示。

圖5 RPWC準則下的塑性功比率-壓力曲線

由圖5可知：當壓力在0～5.74 MPa范圍內時，結構未發生塑性變形，結構塑性功總和為0，因此塑性功比率Rwp=0，相應的曲率也為0；隨著封頭塑性變形量的增大，當封頭塑性總功小于彈性總功，即Rwp<0.5時，曲率示意圖位于曲線的下方，Rwp=0.5對應的內壓載荷值為10.49 MPa；當Rwp>0.5時，曲率示意圖位于曲線的上方，曲線曲率逐漸增大至最大峰值后減小為0，曲率峰值位于塑性功比率-壓力載荷曲線的膝部，對應的塑性壓力值pRPW=12.61 MPa，膝部的出現反應了塑性區逐漸擴展和應力重新分配的過程。

PWC準則判定條件下的內壓-塑性功曲線如圖6所示。

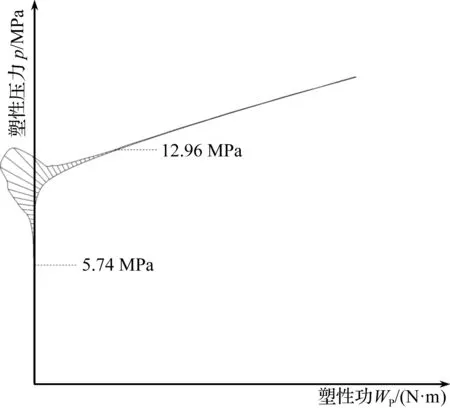
圖6 PWC準則下的壓力-塑性功曲線

由圖6可知：封頭在屈服載荷5.74 MPa時首次發生塑性變形，塑性功和塑性功曲率皆為0；PWC準則判定曲線與RPWC準則判定曲線近似，同樣能反應出封頭在發生塑性垮塌過程中塑性鉸即膝部的形成，隨著內壓載荷的增大，曲線曲率逐漸增大至峰值后減小為0，但曲率等于0的曲線段較長，對塑性壓力結果準確位置的判定存在人為主觀性，曲率零點對應的塑性壓力pPWC=12.96 MPa。

文獻[6]采用了手工作圖的方式找出曲線的零曲率點，為了避除人為主觀因素對零曲率準則判定結果的影響，本文采用CAD建模軟件Pro/E的樣條曲線創建功能和曲率分析功能進行判定，使得ZC準則判定結果更加便捷、客觀。

ZC準則判定條件下的封頭塑性壓力-應變曲線如圖7所示。

圖7 ZC準則下的壓力-應變曲線

由圖7可知：應變硬化分析條件下的封頭最危險節點對應的壓力-應變曲線如圖7（a）所示，根據圖示曲率分布情況，封頭在發生塑性垮塌過程中形成了塑性鉸，且由于塑性流動使大變形效應逐漸明顯，導致了反向曲率的強化部分。第一個零曲率點對應的塑性壓力值pZC=13.20 MPa；

試驗測試條件下的封頭最危險節點位置對應的壓力-應變曲線如圖7（b）所示，第一個零曲率點對應的塑性壓力值pZCT=13.04 MPa。

封頭3種曲率準則的塑性壓力計算結果如表1所示。

表1 封頭的塑性壓力和許用壓力結果

由表1可知：以ZC準則塑性壓力（試驗）結果為參考，RPWC準則塑性壓力相對誤差為3.29%，PWC準則塑性壓力相對誤差為0.61%，ZC準則塑性壓力相對誤差為1.23%。在該封頭模型算例條件下，3種曲率準則塑性壓力計算結果非常接近。

4.3 塑性壓力與尺寸參數關系研究結果

15組封頭模型尺寸的塑性壓力計算結果如表（2～4）所示。

表2 塑性壓力與封頭開孔率關系（iDT=20，itT=1）

表3 塑性壓力與筒體徑厚比關系（idD=0.6，itT=1）

表4 塑性壓力與筒體接管壁厚比關系（idD=0.6，iDT=20）

3種曲率準則下塑性壓力計算結果分別與封頭筒體-接管壁厚比itT，封頭筒體徑厚比iDT，封頭開孔率idD的影響關系如上表所示。

3種曲率準則下的15組封頭模型尺寸計算結果具有一致性。塑性壓力隨著接管開孔率idD的增大而減小；塑性壓力隨著筒體徑厚比iDT的增大而減小；塑性壓力隨著筒體與接管壁厚比itT的增大而增大。

5 比較與討論

（1）由表（2～4）的計算結果可知：同等條件下，ZC準則塑性壓力計算結果大于PWC準則，RPWC準則塑性壓力計算結果最小；

（2）由表（2～4）的計算結果可知：大開孔率idD、大徑厚比iDT、小壁厚比itT對封頭承壓能力有減弱效果；

（3）3種曲率準則在判定方法上具有較大差異：RPWC與PWC判定準則所采用的塑性總功是封頭模型所有單元合集的全局指標，ZC判定準則采用的封頭-接管相貫區最大應力節點應變是以局部指標代表封頭全局；ZC準則局部節點位置的選取具有主觀性和片面性，PWC準則曲率趨近于零點，對應的載荷值取舍具有主觀性，相比RPWC準則實施過程更具客觀性，曲率峰值具有唯一性。

（4）封頭許用壓力[p]=8.41 MPa，為RPWC準則塑性壓力12.61 MPa的1.5倍安全系數所得。

封頭模型算例在許用壓力下的等效應力云圖如圖8所示。

圖8中，黑色塑性區最大應力為110.48 MPa，與屈服極限較接近；少量塑性區受周圍彈性區的包圍限制，封頭結構整體還處于彈性，這表明RPWC塑性壓力計算方法具有參考性。

（5）CLOUD等[13]給出了開孔壓力容器極限壓力pCLD的計算公式，如下所示：

pCLD=λpbv

（1）

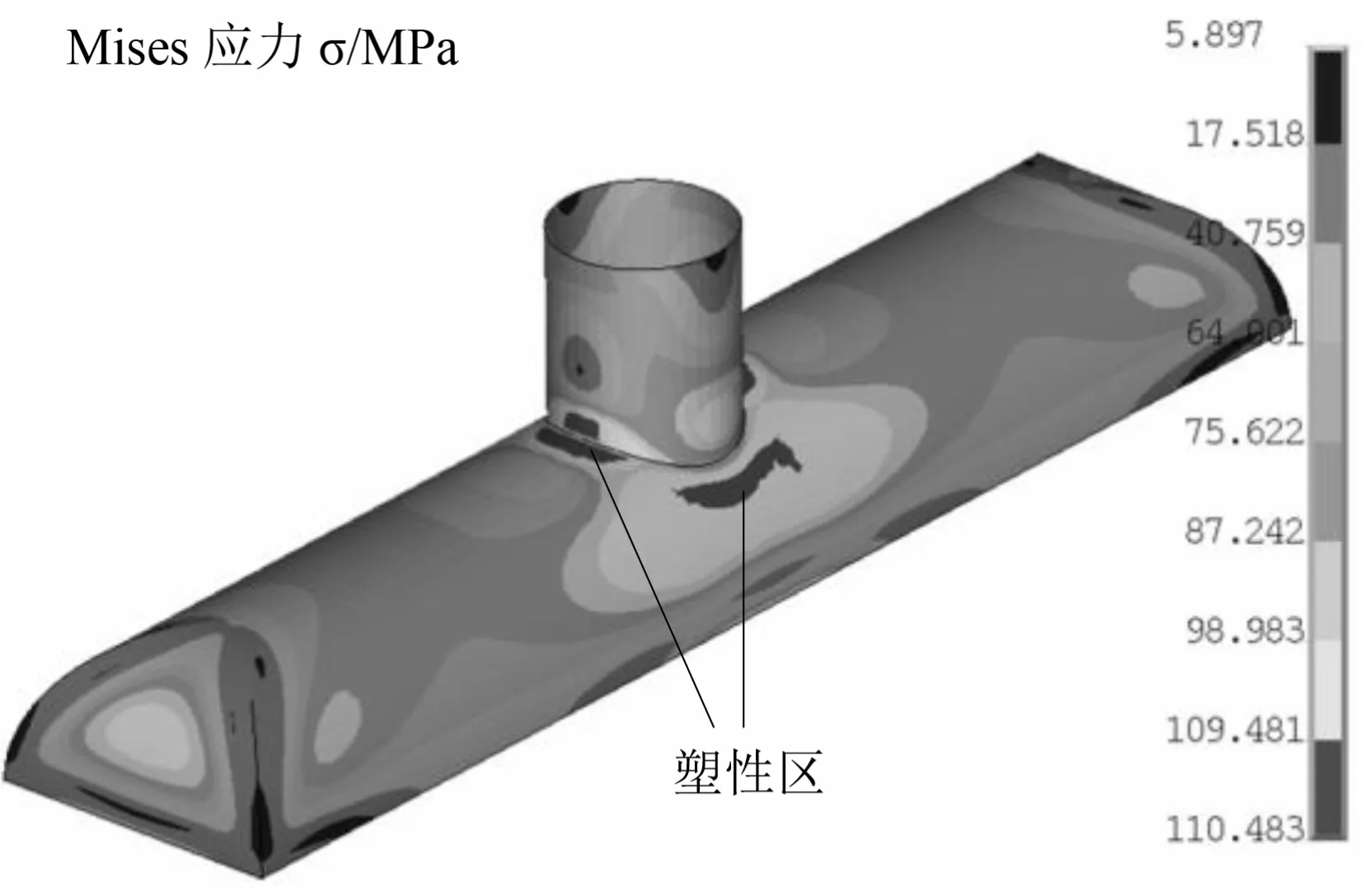
圖8 封頭許用壓力下的等效應力云圖

其中：

式中：d，D—接管和封頭的中徑；t，T—接管和封頭的壁厚；σy—材料的屈服極限。

根據CLOUD計算公式，筆者計算了表（2～4）中15組封頭模型尺寸的pCLD極限壓力。CLOUD極限壓力pCLD要遠小于RPWC準則塑性壓力pRPW，主要原因是極限壓力計算未考慮材料的應變硬化效應，CLOUD計算公式偏保守；pRPW和pCLD計算結果隨開孔率idD、筒體徑厚比iDT、壁厚比itT的變化趨勢具有一致性；這表明RPWC塑性壓力計算方法具有可行性。

為了獲得考慮應變硬化效應的板翅式換熱器封頭塑性壓力計算公式，擬合了封頭塑性壓力計算公式，即：

（2）

擬合公式的計算結果pFIT如表5所示。

表5 FIT與CLOUD公式塑性壓力計算結果

由式（2）的計算結果可知：PFIT與RPWC準則塑性壓力pRPW的相對誤差介于±3.97%之間，具有較好的擬合精度。

6 結束語

本文研究了板翅式換熱器正交接管封頭在ZC準則、PWC準則、RPWC準則下的塑性壓力計算方法，得到以下結論：

（1）通過封頭應變試驗與有限元分析結果的對比，驗證了封頭有限元建模方法的正確性；

（2）RPWC準則塑形壓力判定過程比PWC和ZC準則更具簡便客觀性，且RPWC準則塑形壓力計算結果最小，比PWC和ZC準則更偏安全；

（3）根據RPWC準則塑性壓力及CLOUD極限壓力公式的對比結果，表明了大開孔率idD、大徑厚比iDT、小壁厚比itT對封頭承壓能力有減弱效果；

（4）不考慮應變硬化效應的CLOUD極限壓力公式計算結果偏保守，RPWC準則塑性壓力計算方法更能挖掘真實材料結構的承載潛力；

（5）基于RPWC準則塑形壓力計算方法及應變硬化條件下的板翅式換熱器封頭塑形壓力擬合公式，對封頭設計具有指導意義和參考價值。