突發疫情環境下基于服務水平的應急物流網絡優化設計

劉 明，李穎祖，曹 杰，章 定

(1.南京理工大學經濟管理學院，江蘇 南京 210094；2.徐州工程學院管理工程學院，江蘇 徐州 221018； 3.紐約州立大學奧斯威戈分校商學院，NY13126 美國紐約)

1 引言

近些年，世界范圍內各類突發性疫情時有爆發，如SARS(2003)、人致禽流感(2004)、甲型H1N1流感(2009)、歐洲大腸桿菌疫情(2011)、西非埃博拉疫情(2014-2015)以及2018年8月以來一直在持續發酵的非洲豬瘟疫情等。這些疫情的爆發，不僅嚴重危害人類群眾的健康和安全，也對社會經濟發展造成重大影響。面對各類非常規突發疫情的爆發，如何快速開展應急救援成為重中之重，而在各項應急救援工作中，高效的應急物流網絡設計發揮著重要的支撐作用[1-2]。

國外疫情應急相關研究成果集中于以下兩個方面：①突發疫情環境下的應急物流網絡設計相關研究，主要針對突發疫情擴散環境下，如何布局應急服務設施，以滿足患者的應急醫療資源需求。如Dasaklis[3]從事前、事中、事后三個階段對2012年以前有關突發疫情與應急物流網絡相結合的研究進行了系統綜述。Ekici等[4]建立了疫情擴散與食物分銷選址組合優化模型，并設計了啟發式算法以求解大規模實際問題。He Yuxuan和Liu Nan[5]設計了基于SEIR模型的應急需求預測模型和需求未滿足懲罰函數，并基于此建立了疫情應急物流網絡的線性規劃模型。Liu Ming和Zhang Ding[6]針對流感擴散環境，構建了醫院、配送中心以及供應商之間的醫療資源動態訂購與配送交互式協調優化模型。Dasaklis等[7]針對天花的擴散傳播，構建了大規模接種環境下的應急供應鏈管理模型。②突發疫情環境下的應急物資動態分配相關研究，主要針對突發疫情環境下，如何動態分配有限的應急物資，以獲取最優的救援效果。如針對傳統疫苗分配是以當地居民人口數而不是考慮突發疫情實際狀態這一情形，Teytelman和Larson[8]以H1N1為例，研究了突發疫情環境下的多區域疫苗動態分配問題。Liu Ming等[9]針對突發疫情環境下應急物資不足，構建了全局優化配置模式并與實際中的均衡配置模式進行了效果比對。Chen[10]通過預測抗流感藥物需求量、優化抗流感藥物分配方式和完善疫苗接種方案等措施，實現在流感爆發后疫情應急的有效管理。Buyuktahtakin等[11]針對西非埃博拉疫情，提出了應急資源使用的最優選址分配模型。Brandeau和她的合作者則主要從疾控中心的視角，研究在給定的政府預算條件下，如何動態分配資源以使得HIV、乙肝等傳染病的防控取得最優效果[12-13]。

國內有關疫情應急的研究成果主要集中在該環境下的應急物資調度方面，如劉明和趙林度[14]構建了點對點配送和樞紐輻射配送二者混合協同的配送模式并將其應用于疫情擴散環境下的應急物資配送。王新平和王海燕[15]結合傳染病潛伏期的不確定性所引起的應急救援時滯性，采用縱向配送和橫向轉運相結合的協同配送模式，構建了一類應急物流網絡優化多目標隨機規劃模型。劉德海等[16]從演化博弈的角度，建立突發公共衛生事件的疫情傳播方程，并討論了政府調整相關控制策略對甲型H1N1疫情傳播的影響。朱莉和曹杰[17]以SIR傳染病模型為基礎，構建了一個包含“供應點-中轉點-受災點”的三層應急物流網絡模型。王海軍等[18]利用機會約束方法研究了突發疫情環境下的應急物流選址-路徑問題，建立了在一定應急限制期下時間最小化和成本最小化的雙目標隨機規劃模型并應用遺傳算法進行求解。蔣杰輝和馬良[19]基于Holling-Ⅱ函數的疾病擴散模型，構建了疫情環境下的多目標應急物資配送車輛路徑優化模型并用改進的智能水滴算法進行求解。陳濤和王玉井[20]研究了雄安新區城市化進程中重大傳染病輸入性風險，提出在安全韌性雄安新區構建中，需要進一步協同優化區域公共衛生資源。

在考慮應急服務水平方面，余鵬和雋志才[21]構建了服務水平保證下應急搶修點選址模型并設計了問題求解的拉格朗日算法，其應急服務水平核心是從應急搶修點到其負責維護設備的通行時間小于設定標準的概率要大于某一給定值。何新華等[22]考慮了震后道路中斷條件下應急供應問題與交通路網的協同優化，其應急服務水平的核心是災民需求的及時滿足。張彤等[23]則提出了面向公平分配的時變應急服務覆蓋模型，旨在強調應急服務中的公平性。

與現有的疫情應急物流網絡優化研究成果相比，本文所設計模型具有以下不同之處：(1)定義了一類創新的應急服務水平函數，該函數綜合考慮了感染區域應急物資需求滿足與疫情應急救援成本；(2)建立了基于服務水平的疫情應急物流網絡優化模型，該模型融合了疫情感染區域的人口流動、政府部門的二級環形預防策略以及應急配送中心的服務半徑限制等現實因素。

2 模型構建

2.1 疫情應急物資需求預測

基于江蘇地區2009年H1N1疫情的擴散特征和經典的SEIR傳染病動力學模型[4-6]，考慮到部分患者因病死亡，本文構建了如下的SEIRD倉室模型。該模型將疫情爆發地區的人群分為了5類：易感染者(S)、暴露者(E)、感染者(I)、康復者(R)和死亡者(D)。其中，易感染者通過接觸感染者進入暴露潛伏期，經過一段時間后有明顯發病癥狀從而進入感染者階段，大部分感染者經過治療康復且具有免疫能力，但也有小部分感染者因病毒引發并發癥從而死亡。

圖1 H1N1疫情擴散的SEIRD模型

上述SEIRD模型的假設條件如下：

1)在疫情應急響應過程中，政府雖然會采取強有力的手段控制人口的流動，但顯然不能完全避免，因此考慮人口流動的假設更符合實際情況，而現有文獻大多假設流動人口為易感染者[5-7]，本文亦做同樣處理。

2)不考慮感染區域人口的自然出生率和死亡率。通常這些因素都需要很長時間才能對人口結構有影響，而疫情通常就幾個月時間，因此在本文中不予以考慮。

3)假設政府采取的應急響應策略是對感染者進行隔離治療并對密切接觸者進行二級環形預防，這也是國內外突發公共衛生事件中疾控部門常用的響應策略(如圖2所示)。

圖2 疫情環境下的二級環形預防策略

SEIRD模型涉及的參數及變量定義如下：

參數：

T：疫情持續時間，t=1,2,3,…,T；

K：感染區域集合，k=1,2,3,….,K；

M：其他區域集合，m=1,2,…,M；

βk：感染區域k中疫情的傳染率；

σk：感染區域k中暴露者的發病率；

δk：感染區域k中感染者的死亡率；

γk：感染區域k中感染者的康復率；

θ：每個患者單位時間的應急物資需求量；

n：每個患者的平均密切接觸人數；

η：每個被患者密切接觸的人單位時間的應急物資需求量；

狀態變量：

Sk(t)：t時刻感染區域k的易感染者數量；

Ek(t)：t時刻感染區域k的暴露者數量；

Ik(t)：t時刻感染區域k的感染者數量；

Rk(t)：t時刻感染區域k的康復者數量；

Dk(t)：t時刻感染區域k的死亡者數量；

NIk(t)：t時刻感染區域k的人口流動凈值；

Amk(t)：t時刻從其它m個區域進入感染區域k的人口數，m={Kk}；

Okm(t)：t時刻從感染區域k流出到其它m個區域的人口數，m={Kk}；

dk：區域k的應急物資需求總量。

根據上述假設條件和符號說明，對于任意感染區域k在任意時刻t的疫情擴散行為可以描述為以下差分方程組：

(1)

Sk(t+1)=Sk(t)+NIk(t)-βkSk(t)Ik(t)

(2)

Ek(t+1)=Ek(t)+βkSk(t)Ik(t)-σkEk(t)

(3)

Ik(t+1)=Ik(t)+σkEk(t)-δkIk(t)-γkIk(t)

(4)

Rk(t+1)=Rk(t)+γkIk(t)

(5)

Dk(t+1)=Dk(t)+δkIk(t)

(6)

上述公式(1)表示區域k在t時刻人口的流動凈值等于從其它區域進來的人口流入量之和，減去從該感染區域到其它區域的人口流出量之和。因此，當NIk(t)>0時，表示該區域存在外來人口流入；反之當NIk(t)<0時，表示該區域存在人口向外流失；而當NIk(t)=0時，表示該區域人口處于平衡狀態。公式(2-6)表明對于任意倉室而言，在第t+1時刻的人數等于其在第t時刻的人數，加上在t時刻進入該倉室的人數，并減去在t時刻從該倉室移除的人數。例如公式(2)表示t+1時刻感染區域k中的易感染者數量，等于t時刻該地區已有的易感染者數量Sk(t)，加上t時刻的新增易感染者數量NIk(t)，再減去該時刻已轉化成暴露者的數量βkSk(t)Ik(t)。

對于任意感染區域，在給定各倉室的初始值Sk(0),Ek(0),Ik(0),Rk(0),Dk(0)和相關的參數值后，可以利用上述差分方程組對疫情在該區域的擴散行為進行分析，繼而可以獲得該感染區域的患者人數時間序列數據。不失一般性，定義每個患者單位時間的應急物資需求量為θ，那么t時刻感染區域k中的患者對應急物資的需求量為θIk(t)；同時根據上述符號說明，每個患者的平均密切接觸人數為n，每個被接觸的人單位時間的應急物資需求量為η，則在t時刻的二級環形預防應急物資總需求為n(n+1)ηIk(t)。綜上，感染區域k在整個疫情響應過程中的應急物資需求總量dk等于：

(7)

2.2 應急服務水平函數設計

為刻畫應急服務水平的概念，我們從應急物資需求滿足(應急服務水平1，后文用ESL1表示)與應急救援總成本(應急服務水平2，后文用ESL2表示)兩個方面進行綜合考量，這兩個方面對應急服務水平的影響如圖3所示。

為方便后續應急服務水平函數的表達，首先給出相關參數及變量定義如下：

參數：

Ωmin：疫情應急救援預算下限；

Ωmax：疫情應急救援預算上限；

ωk：區域k的人口數占所有感染區域總人口的比重；

狀態變量：

圖3 應急服務水平組成

hk：第k個感染區域的需求未滿足的比例；

p(hk)：第k個感染區域在ESL1方面的折算值；

f：表示應急救援總成本；

決策變量：

εjk：0-1變量，表示第j個RDC(臨時區域分撥中心)是否給第k個感染區域提供應急物資配送，如果提供，則εjk=1，否則εjk=0；

xjk：第j個RDC給第k個感染區域提供的應急物資量。

在突發疫情應急救援環境下，決策者首先考慮的是各感染區域的應急物資需求滿足，如圖3(a)所示。隨著感染區域應急物資需求的逐漸滿足，ESL1表現為從0到1的S型曲線，反映出應急物資的滿足對應急服務水平的影響是具有參考學習效應的；而當應急物資需求被超額滿足時，ESL1變為常數，意味著多余的應急物資并不能提升應急服務水平。此外，由于區域經濟差異，發達地區人口往往較為密集，因此當其應急物資需求未滿足時，所造成的后果往往更嚴重，為此我們在ESL1的定義中需進一步考慮人口比例的影響。根據上述說明，給出ESL1定義如下：

(8)

(9)

(10)

上述公式(8)給出了第k個感染區域的需求未滿足比例；公式(9)則計算出第k個感染區域在ESL1方面的計算結果，顯然當hk趨于0時，p(hk)趨于1，表明第k個感染區域的應急物資需求基本得到滿足；反之，當hk趨于1時，則p(hk)趨于0，即該區域的應急物資需求基本缺失；公式(10)表明最終的ESL1是由各感染區域k在服務水平1方面的結果p(hk)進行加權求和而得到的。

在圖3(b)中，ESL2進一步考慮應急救援總成本的控制對總體應急服務水平ESL提升的促進作用。盡管在面臨一些非常規突發疫情時，政府會不計成本的進行應急救援(如SARS)，但對于一般疫情應急，決策部門希望應急救援的成本能夠控制在有效的范圍內。如圖3(b)所示，本文將ESL2設計為分段曲線：當應急救援成本小于預算最小值時，意味著此次救援的費用控制在較好的范圍內，ESL2的值為1；當應急救援成本超過預算最小值并逐步增加時，ESL2的值也隨之逐步降低；當應急救援成本超過給定的應急預算上限值時，意味著此次救援的費用超過預期，ESL2的值則為0。根據上述說明，給出ESL2的定義如下：

(11)

式(11)中，f由2.3節中的優化模型求解獲得，參數λ,b給出如下：

(12)

2.3 應急物流網絡設計

大規模突發疫情爆發后，相關部門需要從國家戰略儲備庫(strategic national stockpile, SNS)調撥大量的應急醫療物資配送到各感染區域，從而需要建立一個包含SNS、RDC以及感染區域的三級應急物流網絡。在這個應急物流網絡的構建過程中，決策者的目標是應急服務水平的最大化，具體需要決策的問題包括：(1)各感染區域的應急物資需求滿足情況如何？(2)應急醫療物資從SNS下撥到各感染區域，中間應該設置多少個RDC？(3)每個RDC具體負責哪些感染區域？(4)每個RDC的相對大小是多少？(主要考察該RDC承擔的應急物資量占總體應急物資量的比重)(5)最優的應急救援成本是多少？從優化的角度而言，這是一個連續選址分配決策問題。類似地，我們首先定義模型所需的符號如下：

參數：

I：SNS集合，i=1,2,3,…,I；

J：RDC集合，j=1,2,3,…,J，由于開始并不確定有多少個RDC，因此預先給定一個RDC的上限數J，最優的RDC數可能小于或等于該上限數；

α：應急服務水平權重參數；

Ui：SNSi的供應能力；

(Δk,Γk)：第k個感染區域接收應急醫療物資的位置坐標；

(Λi,Ψi)：第i個SNS的位置坐標；

CTL：從SNS到RDC的單位運輸成本；

CLTL：從RDC到感染區域的單位運輸成本；

Cj：RDC設置的固定成本；

φ：RDC的運營成本系數；

R：RDC的最大配送半徑；

狀態變量：

(xj,yj)：第j個RDC的位置坐標。

Dij：從SNSi到RDCj的應急物資配送距離，為方便計算，統一采用歐式距離；

Djk：從RDCj到第k個感染區域的應急物資配送距離；

sj：第j個RDC的相對規模；

Vj：RDC的運營成本，由RDC的相對規模決定；

決策變量：

zj：0-1變量，表示第j個RDC是否設置，如果設置，則zj=1，否則zj=0；

yij：從第i個SNS給第j個RDC提供的應急物資量；

基于上述符號說明，給出應急物流網絡優化模型如下：

MaxESL=αESL1+(1-α)ESL2

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

εjk≤zj,?j∈J,k∈K

(21)

(22)

(23)

Djk≤R,?k∈K,j∈J

(24)

zj,εjk={0,1},?j∈J,k∈K

(25)

xjk,yij∈R+,?i∈I,j∈J,k∈K

(26)

(xj,yj),?j∈J為實數連續變量

(27)

上述優化模型的目標函數(13)為應急服務水平最大化，權重參數α從側面反映了決策的偏好。α越大，說明決策者更重視應急需求的滿足；α越小，說明決策者更注重應急成本的控制。通過調整α的值，能夠獲得不同的應急物流網絡，以滿足不同疫情等級環境對救援工作的要求。約束條件(14)表示應急響應的總成本，包括應急物資的配送物流成本和RDC的建設及運營成本。約束條件(15)表示RDCj的運營成本是由該RDC的相對規模決定。約束條件(16)給出了RDCj的相對規模計算方式。約束條件(17)表示每個感染區域的應急物資需求僅由一個RDC提供。由于超額的應急物資供給并不能提升應急服務水平，約束條件(18)表示提供給每個感染區域的應急物資量不超過該感染區域的需求量。約束條件(19)表示每個RDC的流量守恒約束。約束條件(20)表示如果供應能力比需求量小，則應急物資都要配送到各感染區域；反之，則按需求量配送對應的應急醫療物資。約束條件(21)表示只有被選擇建立的RDC才能給感染區域提供應急物資配送服務。約束條件(22)表示RDC的數量限制。約束條件(23)表示每個SNS的供應能力約束。約束條件(24)表示RDC的服務半徑限制。約束條件(25-27)表示決策變量的類型。很顯然，由于變量和目標函數的性質，這是一個0-1混合整數非線性規劃模型。值得說明的是，本模型既沒有事先給出確定的RDC數量(如經典的多源韋伯問題情景)，也沒有完全不確定應該建多少個RDC(如經典的集合覆蓋問題情景)，而是基于決策者所擁有的資源和應急管理的經驗等因素，給出了一個RDC數量的上限(見約束條件(22))，這就使得本文所研究的選址分配問題，是介于上述兩類經典問題中間的一種狀態。

3 算法設計

選址分配問題模型通常都是NP問題，難以在短時間內獲得其最優解，而實際應急決策又往往對時效性的要求較高，對應急救援成本最優反而其次。為此，我們設計了一類混合枚舉搜索和遺傳算法的求解方法對該問題進行求解，這種方法能夠保證在短時間內找到一個近似最優解(也有可能是全局最優解)。本文設計的染色體并不是一行數據，而是一個矩陣，其結構如圖4所示。染色體的行數與RDC數量相對應，染色體的前兩列表示RDC的位置(xj,yj)，接下來的I列對應SNS配送到RDC的應急物資量yij，后面的K列數據表示RDC配送到感染區域的應急物資量xjk。對于任意一條染色體而言，當RDC數量給定后，我們隨機生成它們的位置(xj,yj)。當RDC數量和位置均確定后，后續I+K列即為在給定情景下各條線路上的應急物資調度最優解。

圖4 染色體矩陣編碼方式

基于上述染色體設計，給出本文模型的求解算法過程如下：

步驟1：數據輸入及設置。輸入模型中涉及的所有相關參數數據。

步驟2：應急物資需求計算。根據疫情傳播的相關參數和各個疫區的人口結構數據計算出各個疫區的應急物資需求量。

步驟3：給定RDC數量j=1，開始循環。

步驟4：構建初始種群。生成滿足基本條件的初始種群，以目標函數為適應度函數，計算每條染色體的適應度。

步驟5：選擇操作。采用錦標賽選擇法，構建出新的平均適應度值較優的子代種群。

步驟6：交叉操作。采用算術交叉算子，即子代染色體的RDC坐標由父代染色體的坐標數據經算術交叉得到。在獲得新的地理位置后，重新對模型進行求解，比較父代染色體及子代染色體的適應度值，選擇其中較高的兩條染色體保留在種群中，進行下一步操作。

步驟7：變異操作。采用隨機鄰域變異方式，即為染色體中的RDC隨機生成一個它周邊區域的地理位置。同樣的，比較變異前后兩條染色體的適應度值，保留適應度更高的染色體。

步驟8：產生下一代種群。應用精英保留策略，得到下一代種群。

步驟9：判斷收斂條件是否滿足，當最大適應度值和平均適應度值趨于穩定或迭代次數達到預設值時，即終止運算，進入下一步。否則返回步驟5。

步驟10：結束當前計算。記錄最優的染色體及適應度值并返回此結果，該結果為當前情景下的最優結果。

步驟11：j=j+1。判斷j>J，如果是，則算法結束，進入下一步；否則，返回到步驟4，重新開始下一輪計算過程。

步驟12：輸出最終結果。

4 算例測試

為驗證本文模型在實際突發疫情中的應急救援效果，以2009-2010年江蘇省甲型H1N1流感爆發的相關數據為基礎進行算例測試。參考公共衛生科學數據中心及文獻[4,6,9]中提供的數據資料，我們對疫情傳播的相關參數、各疫區的人口結構和位置數據、各SNS的應急物資儲存量和位置數據、相關的成本參數數據、以及遺傳算法的相關參數等進行了統一設置。

4.1 測試結果

通過求解模型，我們首先得到總體的應急服務水平ESL=0.6749，其中第一個部分αESL1=0.5578，第二個部分(1-α)ESL2=0.1171，結合應急服務水平權重參數α取值0.6，則可知ESL1=0.9297、ESL2=0.2926。由于ESL1<1，說明感染區域存在需求未被滿足的情況，表1給出了各個感染區域需求滿足情況。從該表可以看出，由于所設計的應急服務水平函數考慮了不同區域經濟發展水平和人口密集情況，因此蘇南區域(蘇州、無錫、常州、南京等)的需求滿足比例較蘇北區域(徐州、連云港、宿遷等)有明顯的優勢。在突發疫情的應急救援環境下，由于決策者首先考慮的是滿足各個感染區域的應急物資需求，應急救援成本的控制反而其次，因此在本測試當中，ESL2停留于一個較低的水平，這從另外一方面也反映出應急救援服務還有一定的改進空間。

第二，通過模型求解，獲得了突發疫情環境下最優的應急物流網絡，其結構如圖5所示。從圖中可以看出，需要在江蘇區域設置4個RDC，其地理位置及每個RDC的相對規模如表2所示。其中，RDC-1位于連云港市，負責連云港、鹽城的應急物資配送；RDC-2位于揚州市，負責為揚州、泰州、南京、鎮江和常州提供應急物資；RDC-3位于無錫市，負責為無錫、南通和蘇州提供應急物資配送服務；RDC-4位于宿遷市，負責配送徐州、宿遷和淮安這三個疫區的應急物資。在本文中，相對規模表示該RDC所承擔的應急物資量占總體應急物資配送量的比重。從表2中可知，位于揚州的RDC-2需要承擔最大的應急物資周轉配送量(占37.85%)，而位于連云港的RDC-1則承擔了相對較少的應急物資周轉(14.27%)。

表1 各感染區域需求滿足情況

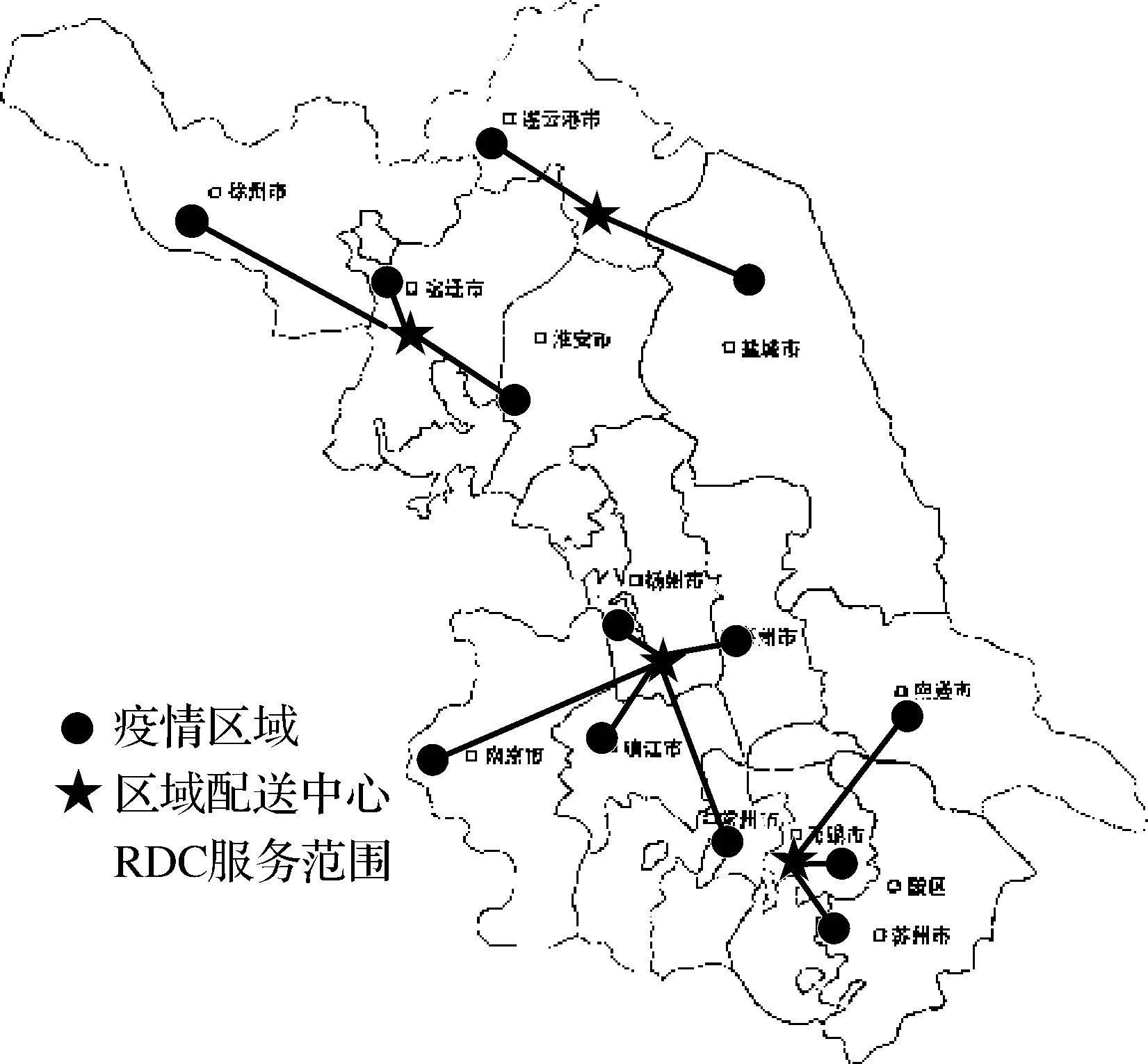
圖5 應急物流網絡結構

表2 RDC的位置和相對大小

第三，通過模型求解，得到應急救援總成本f=6.8295(單位：百萬元，下同)，其中從SNS到RDC段的應急物流成本為4.8398，占比70.86%；從RDC到各感染區域的應急物流成本為1.2754，占比18.67%；RDC的設置及運轉費用為0.7143，占比僅為4.87%。這說明在應急物流網絡的設計中，主要的成本在于應急物資的配送物流過程，而用于應急物資中轉的RDC雖然比例很少，但卻起到很大的節約成本、提升應急服務水平的作用。

4.2 敏感性分析

(1)權重參數α敏感性分析

權重參數α的不同，意味著決策者對應急服務水平的兩個組成部分有著不同的側重。為展示該參數設置對應急服務水平的影響，在不改變其他參數設置的基礎上，本文對其分別取值(0.4，0.5，0.6，0.7，0.8)進行敏感性分析，測試結果如圖6所示。從該圖可知，隨著α的增加，αESL1呈現明顯上升趨勢，而(1-α)ESL2部分有顯著降低，但總體應急服務水平ESL呈現逐步上升的趨勢，反映在實際中即當決策者的優化目標是盡可能地滿足感染區域的應急物資需求時，此時總體應急服務水平能有明顯改善；但相應地，應急救援的成本將大大的增加。在我國的各類災害應急救援過程中，政府部門往往是不計成本的，首先關注的災區百姓的應急救援物資需求滿足，而西方發達國家以及非洲貧困區域的疫情應急救援，卻常常更多的考慮應急救援資金約束。因此，從應急服務水平角度而言，我國現行的應急救援制度具有顯著的優越性，災區百姓有很明顯的獲得感，也正是這種優越的機制，從根本上保障了我國強大的疫情應急救援能力。

圖6 權重參數α敏感性分析結果

(2)應急預算敏感性分析

盡管在我國應急管理的實踐中，決策部門總是把災區群眾的需求滿足置于首位，但這并不意味著應急救援的開展就一定要不計成本。合理的估計應急救援預算，設計節約有效的應急物流網絡，在保障應急服務水平的同時，實現對應急救援成本的有效控制，防止應急救援過程中的各種資源浪費，同樣具有重要的理論和現實意義。為測試應急預算設置的改變對模型求解結果的影響，我們將預算上下限調整為初始值的80%、90%、100%、110%和120%，測試結果如圖7所示。從該圖能明顯地看出，當預算由原先的80%增長到120%時，αESL1的值比較穩定，說明ESL1部分主要受SNS的供應能力影響；(1-α)ESL2部分呈現顯著增長，從而提升了總體應急服務水平ESL。特別地，當應急預算下限為現行設置值的80%時，(1-α)ESL2=0，即ESL2=0，結合應急服務水平函數的定義，說明應急救援成本至少要超過該值，也意味著政府部門至少要撥付對應的應急救援資金，才能保障應急物資的基本供應。

圖7 應急預算敏感性分析結果

(3)RDC數量敏感性分析

在疫情應急物流網絡設計中，如果RDC數量太少，則應急物資需要運輸更長的距離才能到達感染區域；而如果RDC數量太多，則建立和運營RDC的成本又過大；因此，一個優化的應急物流網絡結構往往是上述兩者間的一個帕累托最優。在本文中，我們分別對設置2、3、4、5、6個RDC進行測試，結果如圖8所示。從該圖可以看出，隨著RDC數量的增加，從RDC到感染區域的配送成本呈現明顯下降，而從SNS到RDC的配送成本是先降低后增加，結合RDC本身的設置成本，總的應急救援成本呈現先降低后增加的趨勢，其中設置4座RDC得到的應急救援總成本最低，此時應急服務水平也最高。因此對于決策者而言，在疫情應急物流網絡設計中，需要設置合適數量的RDC，才能夠有效降低救援成本，從而提高應急服務水平。

圖8 RDC數量敏感性分析結果

5 結語

本文以傳染病系統動力學模型和應急選址分配理論為基礎，定義了一類創新的應急服務水平函數，并建立了基于服務水平的疫情應急物流網絡優化模型。該模型具有較好的靈活性和可拓展性，相關部門在應急救援的實際工作中，可以通過調整權重參數有側重地布局應急物流網絡。此外，本文的模型中還充分融合了疫情感染區域的人口流動、不同疫區的人口密度特征、政府部門的二級環形預防策略以及應急配送中心的服務半徑限制等現實因素，因而決策結果具有較好的實踐指導意義。

本文研究的不足之處在于雖然給出了RDC的位置、數量、相對規模等，但并未考慮RDC的容量約束，而在實際運作過程中，配送中心的容量直接影響到應急物流網絡的運作效率和物流系統的總成本。此外，在實際疫情爆發的過程中，由于感染區域政府采取的應急救援方式不同，會對疫情的發展產生影響，因此未來的研究中，還需進一步考慮不同干預手段對疫情發展的影響并將之融入應急物流網絡的設計中。