薄膜表面形貌的相場方法模擬

吳平平 王 冠

(廈門工學院材料科學與工程系,福建 廈門 361021)

0 引言

薄膜材料的表面平整度是衡量薄膜質量的一個重要的指標。而薄膜質量生長的好壞，又在一定程度上決定了表面形貌薄膜的性質及其應用范圍[1]。無論是與光電設備、存儲設備相關的半導體薄膜還是依賴其電學性能應用的鐵電氧化物薄膜，外延生長的薄膜與襯底材料之間不可能保持晶格常數的完全一致，這使得薄膜的內部存在一定程度的錯配應變，當薄膜厚度較低時，薄膜的晶格常數還能與襯底保持一致，這可以稱為理想化的完全匹配(fully commensurate)的晶體薄膜，但當超過某一臨界厚度時，薄膜開始出現松弛(relaxation)現象[4]，同時，由于薄膜生長過程以及表面的起伏等各類因素的作用將在薄膜的內部引入缺陷及位錯，從而使得薄膜的表面粗糙度增加，降低薄膜的質量。因此，為了降低表面粗糙度，提升薄膜質量，研究薄膜的生長過程，預測薄膜的表面形貌，理解錯配應變以及一些輔助緩沖層技術是如何影響薄膜的形貌是十分重要的[5]。

材料的結構組織與形貌特征的研究通常處于微觀范疇，材料的微觀結構能夠影響材料的性能，所以材料微觀結構的設計，如何去優化微觀組織，解決材料中的問題，對材料性能的研究尤為重要。計算模擬是現在一個很好的方法，表現出很多優秀的特點，不僅能夠再現材料結構，還能夠解釋材料結構與材料性能的關系，進而預測部分未知材料的結構與性能以加速新材料的研發。相場計算方法，在計算材料學領域中屬于一類描述介觀尺度材料結構的一類有效的計算方法[7-12]。相場方法常見于模擬枝晶生長的過程[13]，近年來也在鐵性智能材料方面[15]，鐵電、鐵磁和多鐵材料方面[13]，和半導體太陽能薄膜方面[17]等很多材料領域有所應用。由于相場方法是基于材料熱力學/動力學來展開計算，這使得該計算方法具有相當現實的物理意義。使用相場方法可以避免跟蹤界面[7]，從而使得相場方法在材料結構模擬方面得到了很廣泛的應用，而相場方法所涉及的自由能表達式(及部分參數)可以與具體實驗結果相匹配，使得相場方法在近年來同時受到廣大理論工作者與實驗工作者的偏愛。目前文獻中已有相當多的相場計算方法相關的綜述文章[7-12]與專著[18]，相場方法也已經拓展到各種不同的材料物理性質的模擬與計算。通過引入包含錯配應變效應的彈性能進入熱力學自由能計算，使得相場方法在研究模擬薄膜表面形貌特征方面也有了廣泛的應用。本文將把焦點定位在相場方法模擬薄膜生長與薄膜表面形貌領域，首先簡單的回顧了薄膜生長的幾種主要的模式，著重描述了一下臨界厚度問題以及薄膜表面存在的ATG不穩定性問題。隨后，概括了相場方法求解此類問題的一般性過程。然后重點介紹部分是近十余年來相場方法在計算薄膜表面問題，薄膜生長問題方面的一系列研究成果，以及處理各類問題時對相場方法進行的改進與發展，并同時討論了相場方法對薄膜中的缺陷問題和多層薄膜問題所做的一部分工作。最后給出總結以及未來相場方法在研究此類問題的突破點與展望。

1 薄膜生長

光電薄膜器件在太陽能方面不斷發展，薄膜太陽能電池作為一種光電功能薄膜，可以解決能源短缺問題且無污染易于推廣[20]。薄膜太陽能電池有多種，按材料可分為硅薄膜型、化合物半導體薄膜型和有機薄膜型。 化合物半導體的光電特性與材料表面的平整度有很密切的聯系，例如，制備表面平整的高質量InGaAs薄膜，對于InGaAs半導體光電器件有著極其重要的意義。而InGaAs與GaAs襯底之間存在晶格失配應力，制備高質量的InGaAs薄膜一直是研究的熱點與難點[21]。所以，研究薄膜的生長過程，對于理解薄膜性能，具有重要的意義。

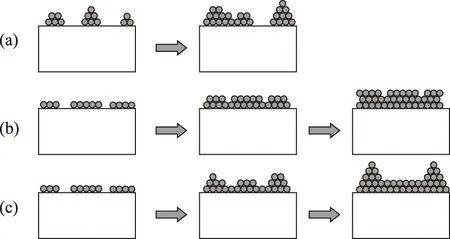
圖1 3種主要的薄膜生長模式(a) 島狀生長模式; (b) 層狀生長模式; (c) 層-島狀混合生長模式

首先我們介紹薄膜生長的幾種主要過程，為了能夠得到單層的薄膜結構，往往可以使用分子束外延(molecular beam epitaxy, MBE)方法[22]，通過氣相技術生長外延薄膜。一般認為，Ernst Bauer在1958年首先分類總結出了3種主要的薄膜生長模式[24]，如圖1所示。(a)島狀生長模式，又稱為Volmer-Weber生長，這種生長模式下，首先在薄膜的襯底上原子會聚集，并逐漸形成一個小島狀的結構，薄膜原子和原子之間的作用力要比原子與襯底材料之間的作用力更強，而從熱力學的角度上來說，這種生長模式提供了更多的表面能，往往適用于薄膜材料與襯底材料之間晶格常數相差較大的情況下，這是由于較大的晶格常數差距將引起巨大的錯配應變并產生較大的彈性能，所以島狀生長模式雖然增加了表面能，但是卻能極大幅度降低薄膜材料內部的彈性能，從而使得總自由能降低。這種生長方式在半導體材料上尤為常見，如Si/Ge系統，InAs/GaAs系統中都可以觀察到此類生長。這種生長方式最大的缺點在于很容易使得薄膜表面非常不平整。(b)層狀生長模式，又稱為Frank-Van der Merwe生長；這種生長模式下，薄膜材料首先在襯底上生長成為薄薄的一層，當這樣的一種單原子薄層生長完成之后，再在第一層的基礎上生長第二層原子層，這說明了薄膜材料對襯底之間的作用力更強，明顯應大于薄膜原子與原子之間的作用力，這種生長方式在氧化物薄膜生長中較為常見，這種生長方式也稱為二維生長。(c)層-島狀混合生長模式，又稱為Stranski-Krastanov生長[25]，是由Stranski和Krastanov在1958年發現的。在這種生長模式下，薄膜材料首先被襯底材料所吸附，從而在襯底上生長成為了薄薄的幾層原子層，但當超過一定的臨界厚度時，在薄膜的這幾層原子層上，薄膜繼續生長時，開始了島狀生長的模式，從熱力學的角度來說，首先薄膜的晶格常數往往是和襯底的晶格常數相匹配的，當薄膜的厚度低于臨界厚度時，整體的應變能較低，但當厚度達到臨界厚度時，應變能達到一個臨界值，此時，薄膜的上表面開始發生松弛現象(relaxation)，松弛將很容易引入位錯，位錯的引入可以降低應變能，這里應變能的降低幅度一般可以遠超過薄膜進行島狀生長所引入的表面能增加，使得后一階段的生長模式進入島狀生長模式。這類生長模式應為最常見的模式，在各類薄膜生長的過程中都有觀察得到。

所以說，當薄膜厚度太高時，位錯和缺陷就不可避免，這時如果考慮完美晶體的情況，就需要注意到薄膜的臨界厚度，對于薄膜臨界厚度的討論，最經典的兩種理論來自于Matthews-Blakeslee (MB)理論[26]以及People-Bean (PB)理論[27]。其中，根據Matthews and Blakeslee’s (M&B’s)的理論指出，外延薄膜的臨界厚度為

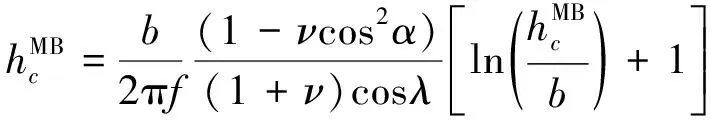
(1a)

其中hc是臨界厚度，ν是泊松比，f∈mf=(af-as)/as是薄膜的錯配應變，其中af和as分別是薄膜和襯底的晶格常數。b是伯克斯矢量的尺寸，α代表了位錯線與伯克斯矢量的夾角，λ代表了滑移方向與薄膜平面內垂直于滑移面與界面交線的方向的夾角。假設ν=1/3，b=4?，cosα=1/2，cosλ=1/2。公式可以簡化為

(1b)

而People-Bean理論提出外延薄膜的臨界厚度是

(2a)

他們假設以GexSi1-x合金為例，b=4?，a平均值為5.54?。可得

(2b)

最初的MB理論和PB理論大多建立在金屬-半導體薄膜體系之中，為了更準確的描述氧化物薄膜中的臨界厚度，Speck和Pompe改良了MB模型[28]，同樣的Maree等人改良了PB模型[29]，可以得到

這里的β表示錯切參數描述缺陷核的次連續能量。改良后的模型可以更好地與氧化物類型的薄膜進行比對。從而在氧化物薄膜材料方面有一定的應用[30]。

為了更直觀的演示與比較兩個模型的區別，根據相關的文獻[32-34]，圖2所示為對數坐標下MB模型和PB模型的預測值以及相關的實驗觀測值。圖中可以很明顯的看到，兩個模型均有相關的實驗數據可以與理論預測值對照。而這兩個模型也一直存在爭議。其中MB模型是最受到廣泛接受的，也是能夠與實驗成功對照最多的模型。PB模型受到廣泛關注主要是因為一些SiGe/Si系統和InGaAs/GaAs系統的實驗結果可以很好的與PB模型對照。然而，需要注意的是，很多實驗，尤其是早期的實驗，均存在不同程度的松弛效應，而松弛效應并未考慮在模型里[35]。

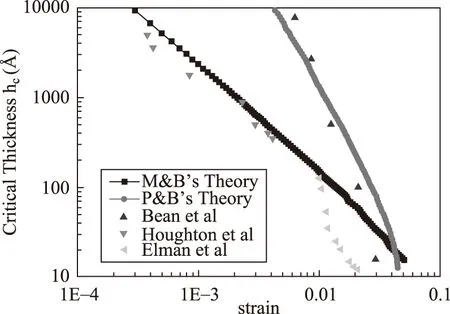
圖2 MB模型，PB模型對臨界厚度的預測值與實驗值[32-34] 的比較

同時，我們還應關注在薄膜生長過程中，臨界厚度hc處薄膜表面由于應力作用產生的波動，薄膜表面的波動很容易導致局域表面的彎曲，從而導致原子在起伏的表面上堆積形成層-島(S-K)生長模式，這種生長模式上的島是由于彈性不穩定性導致的，從而島的晶格常數和塊體的一致。這種彈性不穩定性往往被稱為ATG不穩定性，它首先是由Asaro, Tiller以及Grinfeld (ATG)[36]所發現的，這種一致性的島狀生長是沒有缺陷的，這使得這類島狀生長在納米電子與光電子器件當中有很強的應用潛力，但這里請注意，這種應變不穩定性會隨著島間的空間減小而降低。對于單位面積島密度較高的薄膜來說，島與島之間間隔較小，隨著沉積的進一步發生，島與島之間相連時，很容易產生缺陷或者位錯環，從而導致島上出現缺陷[38]。通過線性的不穩定性分析，可以預測臨界波長以及最快的生長速度[39,40]。而表面的最終形貌，需要取決于不同波長的表面波共同作用的結果。ATG穩定性在各類系統和條件下都有所報道，例如4He的固液界面[41]，Si襯底上的SiGe薄膜[42]，聚合物基體上的聚合物薄膜[43]，金屬薄膜[44]等。ATG現象的產生最基本的解釋可以如圖3所示[45]，如果薄膜的表面是平整的，那么表面是無法松弛的，然而，一旦表面開始振蕩，波峰處的應變就可以得到松弛，波谷處的應力反而會集中，這樣使得波動進一步加劇，如果還同時考慮氣相沉積的過程，那么原子則更有可能沉積在波峰處，同樣導致波動加劇。

2 相場計算方法

為了描述在某一特定材料襯底上外延生長的薄膜，最簡單的情形是引入3種不同的序參量來表示空氣層(η1)，薄膜層(η2)以及襯底層(η3)，有些計算會考慮到緩沖層(η4)。ηi分別指代的是這幾相在某個位置的體積百分含量，這樣對于系統中的任意一處，序參量的總和應等于1，亦即

(5)

介于兩個序參量ηi和ηj的界面定義為γij。一個最基本的描述形貌的相場模型，所考慮的系統的總自由能應該包括化學能，表面能和彈性能

Ftotal=Fchem+Finter+Felas

(6)

其中，朗道形式的化學能表達展開是

(7)

這里的ωij是雙勢阱的最高點，V是系統的總體積。系統的總界面能需要考慮到每兩個序參量的界面的總和，這樣總界面能可以寫成

(8)

這里的αij是梯度能系數。這里的梯度能系數，可以通過實驗過程中所得到的界面能，或者第一性原理計算得到的界面能來反向推導得到。薄膜在某一特定的應力狀態下的彈性能可以使用Khachaturyan的微彈性理論計算[46]

(9)

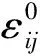
對于一個守恒系統，在砷化鎵襯底上的InxGa1-xAs薄膜表面形態生長的時間演化是由非線性Cahn- Hilliard方程支配

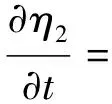
(10)

考慮薄膜的生長情況下，可以在方程的右側增加一項[47]

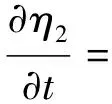
(11)

其中M是動力學系數，t是時間，這里的η2表示描述薄膜的序參量，t是時間，方程右邊的第二項Vdnyχ描述的是薄膜的生長，其中Vd是沉積速率，χ是一個隨機數，ny是表面的法線方向，也就是說

(12)

我們的模擬中，如果我們考慮一個穩定的靜態情況，那么Vd這一項應該為零。僅僅當研究薄膜沉積現象時，Vd應為一個有限值，即具體的沉積速率大小。這樣，計算得到各分能量，然后求得總能量Ftotal的大小，代入相場方程迭代求解，求解方程時既可以使用差分方法，或者使用半隱性傅里葉譜方法[48]，以加快計算速度并保持相對的穩定。η3是一個固定的襯底結構，并不會隨時間演化，而空氣相η1可以通過公式(1)計算得到。

如果考慮到材料內部成分的問題，可以同時考慮成分場c(r,t)以及相場η(r,t)兩個場，來計算得到材料的相分布以及成分分布

如果考慮存在缺陷以及缺陷移動問題，一個動態的缺陷場是必不可少的，使用Gingzburg-Landau方程(Allen-Cahn)可以很好地描述缺陷場的變化

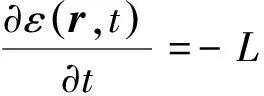
(15)

其中L是動力學系數。對于求解帶有緩沖層的薄膜結構，我們通過同時求解多序參量以為核心的Cahn-Hilliard(CH) 方程：

這里需要注意到的一點是，如果采用多序參量進行計算的話，不僅僅朗道能以及界面能的能量計算較為復雜，需要更多的相關參數，更為重要的是，計算的復雜性以及誤差出錯的可能性也大大增加，一種較為簡化的替代方式是，一般而言，多層結構是在一層完成后再添加另一層，這樣相隔一層的兩層材料之間可能會有接觸并考慮其界面問題，但相隔兩層的材料之間接觸的可能性就大大降低，這樣聯合求解雙CH方程并不斷重復，就可以得到整個系統的表面以及界面結構。當然對于一些超晶格、周期性、不考慮表面(或襯底)效應的薄膜多層結構，也可以僅使用一個序參量來區分兩類不同的薄膜結構。

在模擬中，大多數材料所使用的重要參數，如晶格常數，彈性系數，錯配應變等可以盡可能地使用實驗工作文獻的數據，部分未知材料的參數可以使用相關材料的參數估算。我們以GaAs和InAs為例，其彈性常數來源于實驗[49，50]。 而InxGa1-xAs的彈性系數可以使用線性插值法得到。通過選擇計算過程中使用的化學能系數，梯度能系數和Cahn-Hilliard方程的動力學系數，可以調整計算的空間尺寸與時間尺寸使之與實際實驗過程對照。對于薄膜體系中，一般在薄膜平面內應用周期性的邊界條件。計算過程中，可以使用了兩種平面波來描述薄膜的表面。一種假設是表面形態是靜態的正弦波，這樣薄膜厚度h(x)為

h(x)=h0+βsin(kx+φ)

(18)

其中h0是初始平均薄膜厚度，β是振幅，k是波數，和φ是初始平面波相位。而如果采用隨機表面，我們認為隨機表面是n個正弦波的疊加：

(19)

其中m是波型的數量，第m列波所對應的振幅，波數，和平面波相位分別為βm，km和φm。

為了表征固態薄膜的表面平整程度，使用了均方根粗糙度(RMS)，它可以定義為

(20)

3 薄膜表面的相場計算方法進展

相比理論模型來說，相場方法的優勢在于可以避免追蹤界面，依據自由能極小值優化獲得薄膜的表面界面形貌。通過界面穩定性來與實驗結果進行比對。起到解釋實驗機理，優化實驗手段的效果。在薄膜生長模式方面，尤其是在半導體材料中，島狀生長模式或者層-島狀生長模式較為常見，具體生長情況取決于生長速度與薄膜的平面內應變大小。近年來相場模擬中兩類生長均有報道，與實驗結果也符合較好。Liu等人[51]首先報道了外延島狀生長的薄膜表面形貌。控制生長的層數以及生長速度可以獲得不同的薄膜表面形貌。Takaki等人[47]在動力學相場計算方法，引入了生長速度項，觀察到了層-島狀生長模式的半導體薄膜生長。Voigt等人[52]的研究也指出，在生長過程中，部分薄膜由于應變分布不均勻等現象導致局域應變過大，斷裂形成島狀-層狀的混合生長，亦即SK生長模式，Szlufarska 等人[53]在InGaAs材料的模擬也觀察到了SK類型的薄膜生長，說明相場計算和已知的實驗報道是保持一致的。在臨界厚度的預測方面相場模擬的工作較少，近年來，為了解決薄膜松弛問題，相場方法也開展了一些工作來驗證經典理論。Sheng[30]和Podmaniczky[54]分別使用了經典相場動力學方法和相場晶體方法對比了相場計算得到的臨界厚度與MB理論、PB理論的對比結果。對比結果顯示相場計算模擬的結果與PB理論所預測的數值一致性較高。預測薄膜的ATG不穩定性正是相場方法的優勢所在。相場方法因為不預先假定界面，不追蹤界面等優勢，可以直接模擬薄膜的表面形貌并與實驗進行對比。這里需要注意的是，ATG不穩定性是由界面能和應變能兩類能量相互制衡所導致的，所以，在相場的理論模型中，必須考慮應變能的作用。薄膜表面形貌及ATG不穩定性的一些細節作者在下面的3.1節中進行了詳細的描述。

3.1 薄膜形貌

Khachaturyan等人應用了其微彈性理論[55]，研究了表面的不穩定性問題。通過假設表面形貌為一個隨機的疊加波，觀察其表面隨著時間流逝而發生的形貌變化。研究顯示，在存在錯配應變的情況下，一個較薄的薄膜表面會首先形成溝壑，隨著時間演化使得表面呈現自發組織的納米點結構。該結構的形成來源于自由能的極小值，提升的表面能可以有效地降低材料內部的彈性能，最終形成了納米點結構。進而通過彈性能作用引入多重正弦波疊加的隨機表面，則會最終形成了納米島結構。

Hu等人則研究了納米點結構的大小以及表面能/界面能對納米點結構的影響[56]。其研究中所示，隨著襯底/薄膜之間的界面能量增大，納米點切面與襯底平面的夾角不斷增大，從而影響了納米點的形貌與尺寸，進一步的研究顯示，表面角與納米點的尺寸是成正比的，表面角的增大意味著納米點的尺寸也在增大。Hu等人同時研究了薄膜中存在的調幅分解問題，通過調整或控制不同的薄膜的彈性系數與剪切應變，也可以很好地控制自發分解所得到的粒子的尺寸，獲得的薄膜表面的自發分解圖案可以更直觀體現。模擬結構結果顯示，可以應用錯切方式(miscut)來控制粒子的大小與形貌[57]。

平面內應變對納米點的形貌、結構是至關重要的，絕大部分的平面內應變是xy方向等同的，當然不同襯底上不同方向上生長的薄膜，xy方向上的剪切應變或許會不一致。Ni等人通過設置不同的剪切應變，來改變納米點的形貌，以達到其應用價值[58]。在其實驗中通過模擬不同方向上(x和y)的不同錯配應變(0，0.02) 以及(0.02，-0.02)所觀察而得出有意思的情況。如果僅一方向上存在拉伸應變，薄膜呈現波紋形狀，而在一方向拉伸，另一方向壓縮，則容易出現納米點與納米線同時存在的情況。

Tomita等人在薄膜形貌上考慮了薄膜生長的因素，在Cahn-Hilliard方程中引入沉積速率，如公式(11)[47]。研究在某一恒定沉積速率下Vd=1×10-11m/s 下不同初始形貌、不同界面能所導致的納米點形貌、結構以及尺寸的變化情況。Tomita闡述了在時間演化下島狀生長過程，不僅演示出了納米點的形貌，也同時給出了x方向上正應力場的分布，還展現出在不同薄膜-襯底的界面能情況下的效果[47]。Wang等人也采用相場模擬技術，在鎵砷襯底上逐步生長出In0.3Ga0.7As薄膜的過程，如圖4所示[17]。

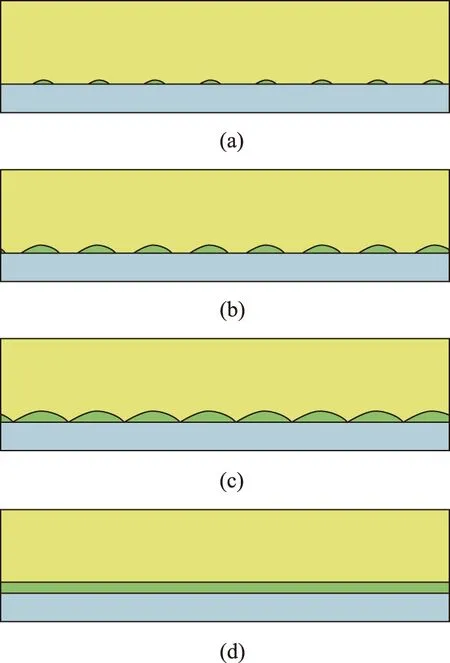
圖4 在GaAs襯底上In0.3Ga0.7As薄膜的生長

除了了解薄膜的表面形貌特征，對于不同形貌的元素分布，也會影響相關材料器件的特性。Ni等人[59]通過同時求解方程相場方程(13)、濃度場方程(14)，可以很好地描述不同形貌的納米點結構下的濃度變化。實驗采用金字塔、拱頂、截斷金字塔形納米點的濃度場分布，用來表示Ge原子偏好聚集在量子點結構的頂部、角落、尖端等地，而靠近襯底，三相交點的連接部分濃度較低[59]。

吉野雅彥等人在襯底上加工設計了一系列的凹槽，研究在此上生長金薄膜納米點的形貌[60]。通過兩者不同的過程，可以生長得到僅在平臺表面的規則分布納米點結構以及分別在平臺和凹槽都有分布的納米點結構。這樣，可以通過凹槽誘導的方式來生長排列規則整齊的納米點材料。

而Martin Grant等人開創出相場晶體方法[61]，也包含了薄膜表面模擬的機制。他提出隨著薄膜的不斷生長，溝壑開始出現，如果不能控制納米點之間的間隙，空洞有可能在薄膜內部出現，從而形成缺陷。相場晶體方法的優勢在于可以很直接的看到原子在薄膜表面的累積過程，這一過程可以很清晰[61]。

近年來，Wang等人在模擬薄膜生長的過程中，同時考慮了調幅分解引起的界面不穩定性問題[62]，通過引入不均衡應變來描述不同相之間的應變差值

(21)

模擬結果顯示沒有錯配應變，隨著時間推移，在薄膜中的雙相自發分解過程中存在3%錯配應變時以及沒有宏觀錯配應變但存在1%相錯配應變時的情形，與沒有錯配應變的對比情形[62]。

Wang等人繼而結合實驗工作研究了一類襯底上帶有貼片的自組織納米點結構[63]。實驗結果表明，貼片確實有助于自組織納米點的形成，然而貼片中是否存在應變問題。會影響到納米點結構的形貌生長與數量。貼片帶有應變的情況下，納米點的形貌更加飽滿也會與靠貼片更近一些。其實驗研究電鏡圖也說明了這一點。

3.2 缺陷對薄膜表面的影響

有關半導體外延薄膜中的缺陷問題，尤其是位錯問題，對半導體薄膜的質量來說尤為重要，在已有的薄膜相場模擬中加入缺陷或者位錯的影響，可以使相場模擬的結果更加真實[65]。在計算相結構、表面結構的基礎上，再把應變本身作為序參量，通過Ginzburg-Landau方程演化，可以描述應變分布，以及應變分布隨時間的演化結果。Khachaturyan等人同時求解相場(方程(13))及應變場(方程(15))來獲得線缺陷隨著應力松弛效應的移動軌跡，他為我們清晰明確的表明錯配應變在薄膜和襯底中隨著時間的流逝所經過的一系類位置變化。同時還可以描述不同情況下Frank-Read源在厚襯底、薄襯底以及多層膜之間的詳細的擴散情況，這些位錯源隨時間演化的擴散形貌各不相同[66]。

Zhuang等人通過在相場動力學方程中植入有限元網格的方法，也可以獲得很好的效果[67]。可以很好地顯示位錯線的分布，并同時展示薄膜材料表面的位移以及變形情況，從而可以很好地預測薄膜表面的缺陷，裂紋等力學現象。還為大家直觀的體現出薄膜表面在Z方向上的放大位移的情況。

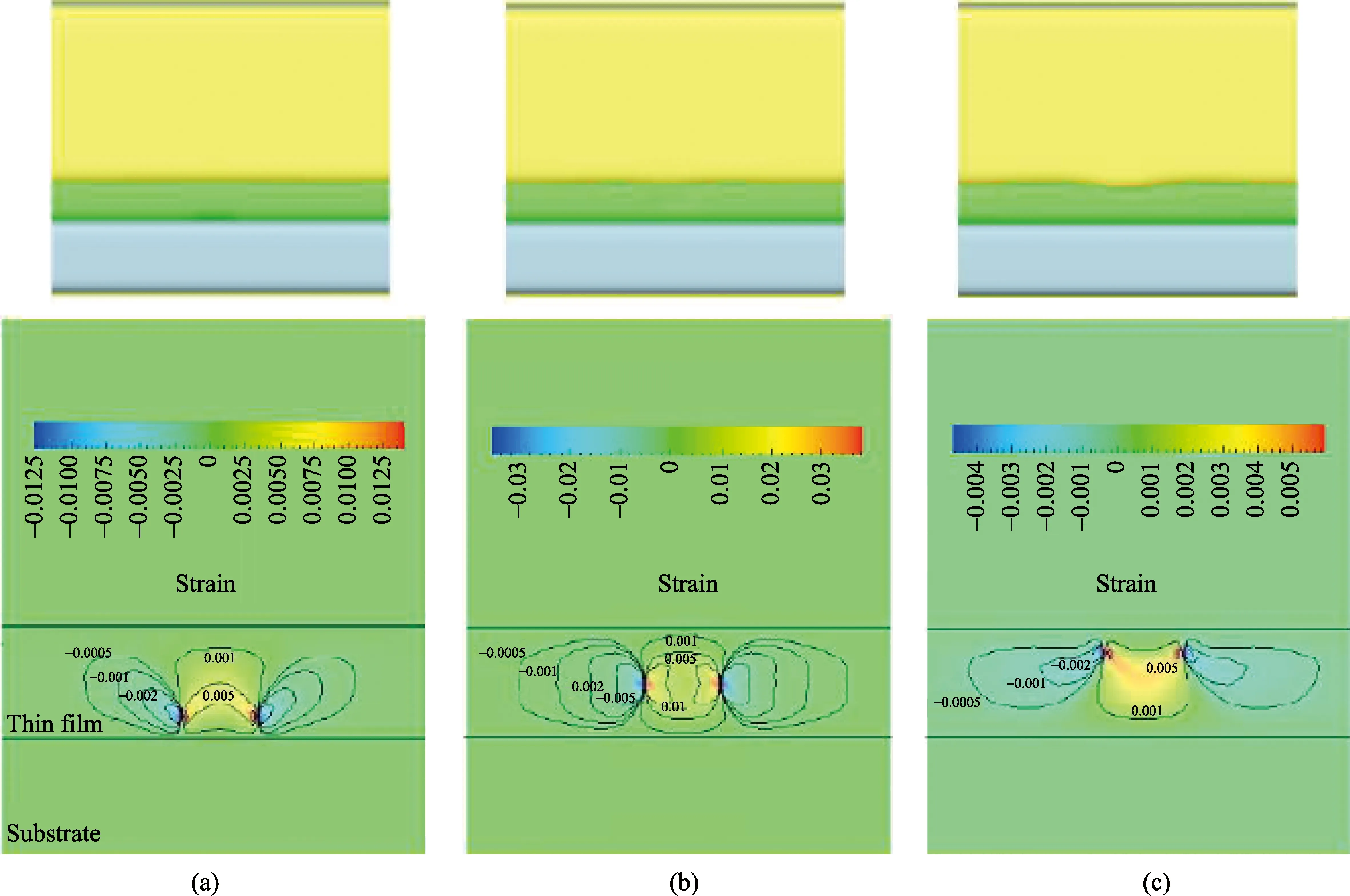
圖5 當缺陷位于薄膜的底部、中部、以及頂部時所引起的表面形貌的變化以及相關的應變場的分布狀態

Chen等人也將位錯應用于薄膜與襯底之間的界面處，繼而研究薄膜中的自發分解問題。采用控制變量的方法，在保持薄膜的厚度不變，使xy方向上界面處缺陷數量改變，得出不同的自發分解的結構情況。研究結果顯示，薄膜中的調幅分解，很大程度上會受到界面處的錯配應變的影響。在界面處的很少的缺陷，就可以引發很明顯的自發分解結構的變化。表面形貌與結構可以隨著缺陷的密度，薄膜的厚度而發生變化[68]。通過調整或控制薄膜的彈性系數與剪切應變，可以很好的控制自發分解所得到的粒子的尺寸。這可以應用于錯切方式(miscut)來控制粒子的大小與形貌[69]。

Grant等人使用了晶體相場方法研究了帶缺陷的薄膜與不帶缺陷薄膜的形貌[70]，對于與襯底之間存在一定的錯配應變的情況，表面粗化以及界面能增加是不可避免的，然而他們發現，帶缺陷的薄膜在一定程度上可以抑制薄膜表面溝壑的生長速度，模擬出兩種分別是帶有缺陷以及沒有缺陷的情況，事實上，在納米島的表面形成缺陷后，應力集中導致彈性能增大取代了表面能的增加。這一點與生長速度以及薄膜和襯底之間錯配應變的關系非常密切。

Wu等人研究了處在界面，薄膜內部，以及接近薄膜表面處的缺陷對薄膜表面形貌的影響，如圖5所示。很明顯的接近薄膜表面的缺陷對薄膜的影響很大。缺陷的尺寸，密度等對薄膜的表面粗糙度也有不同程度的影響，帶有缺陷機制的3維結構表面形貌的計算結果與實驗結果相比非常類似[55]。

3.3 多層薄膜問題

在一些實際的應用體系中，多層薄膜往往是常見的，Gururajan等人最先研究了多層薄膜中的形貌界面不穩定性問題[72]。在他們的研究中，多層薄膜形貌發生彎曲，進而發生斷裂是一個常見的情況。他的實驗為我們呈現出的一個關于簡單的三層薄膜的例子，在這個薄膜所顯示的不同的形貌，一個相對較軟較薄，另一個相對較硬較厚，經過實驗演化，從開始不穩定狀況到薄膜發生斷裂的形貌的對比過程。而其中彈性各向異性、薄膜厚度、薄膜的體積百分比以及薄膜之間的間隔，都有可能會引起薄膜表面的不穩定性，進而發生薄膜斷裂問題。Zaeem等人使用了有限元方法耦合相場動力學，并引入彈性能[73]。計算了5層薄膜所能展現的不同演化結構，類型Ⅰ-Ⅳ分別顯示了不同條件下的多層薄膜演化結果。薄膜有可能斷裂變成顆粒形貌(類型Ⅰ)，也有可能某一條消失，另一條擴展(類型Ⅱ)，或者合并(類型Ⅲ)，或者合并并擴散(類型Ⅳ)。作者可以根據不同的條件得到演化相圖。

這里請注意上述所提到的多層薄膜均是兩相結構的薄膜。為了解決在半導體薄膜中使用的緩沖層技術以及多層緩沖層技術，Wu等人在原有的三個序參量的基礎上加入第4個序參量以描述緩沖層結構[74]。這樣通過聯解雙Cahn-Hilliard方程可以很好的分析帶有緩沖層結構的多層薄膜體系的應力、應變、表面等等各類問題。研究顯示，隨著緩沖層厚度的增加，薄膜的表面粗糙度不斷的降低，如圖6所示[75]。

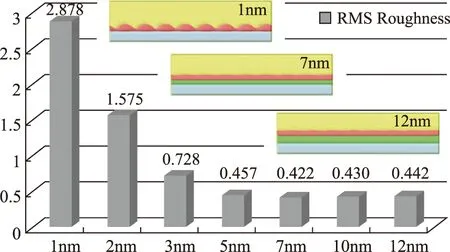
圖6 隨著緩沖層厚度的增加，薄膜的表面粗糙度不斷降低

這個模型也可以進一步的拓展成多序參量結構，用來模擬量子阱、量子點結構或者并設計新一代的緩沖層結構、多層緩沖層結構以及梯度緩沖層結構，或進一步研究緩沖層的緩沖機制。

4 結語

薄膜表面以及薄膜生長決定了薄膜質量，在相場方法中考慮彈性能以及彈性效應，可以很好地描述薄膜的表面形貌，內部的應力應變分布，一定情況下還可以描述一些原子濃度，相分離，缺陷影響等特征。本文首先介紹了薄膜生長的基礎，包括生長模式、臨界厚度以及ATG表面不穩定性。通過基本的相場計算模型，重點介紹了近年來相場方法與經典理論的對照，及其應用在研究薄膜表面、缺陷薄膜作用以及多層薄膜情況。從已有的研究中我們可以看出，相場方法已經可以很好地與實驗相比對，描述薄膜的形貌以及相關的物理性能，未來相場方法在模擬薄膜方面的發展應側重于應用和預測材料性質方面：

4.1 多場的聯合效應

從上述的研究工作我們可以看出，聯合多場進行相場動力學計算，是當前相場計算發展的一大趨勢。多場聯合計算的好處更加全面、詳細，而且考慮到不同場之間的相互作用時會更加接近真實情況。但是缺點也非常明顯，其一就是計算量太大，所以多場方程聯合求解如何優化計算是一個主要問題。其二是程序開發周期或許會延長，一些界面友好的相場計算軟件(如μ-pro[76])，或許可以較好的解決這類問題。

4.2 基因組計算

對于材料應用來說，開發新型材料或者設計新型材料結構尤為重要，然而，完全通過實驗手段開發新材料自然需要很高的成本，通過材料計算的方法進行一個大致方向上的預測，就顯得尤為重要。相場動力學方法的一大優勢在于可以很好的結合實驗工作，獲取實驗參數或者根據第一性原理計算獲得基本參數，從而實現與實驗結果的高度匹配。同時相場方法還可以顯示結構，耦合缺陷等一系列材料中的問題，并可以從統計意義上給出宏觀性質。根據一系列參數進行高通量計算建立相關基因組數據庫，包含材料結構，宏觀性質，缺陷分布等是相場方法在近年來的首要任務。

4.3 機器學習的應用

基因組計算的目的是為了更快的找到適合的材料。而使用近年來興起的機器學習技術，可以更快的更方便的找到新型材料。可以有兩種途徑達到尋找適合材料或者新材料的目的。(1)通過相場方法，建立材料基因組數據庫，通過機器學習，滿足適合條件的方法在數據庫中找到新型材料。(2)從某一特殊點開始，通過相場方法計算出材料的性質，衡量與目標材料性質的差距，通過機器學習的方式，改變或調整初始條件，慢慢逼近目標材料所需要的特性。當然前一種方法的耗時較短，覆蓋范圍大，但建基因組數據庫工程量大，后一種方法目的性強，靈活性強，不需要預先建立數據庫。這兩類方法都有自己的特點和優勢，可以應用在不同場合。