基于時間序列分析的單采血小板臨床需求預測模型研究

彭榮榮 劉蕓男 楊小麗* 楊冬燕

(1.重慶醫科大學公共衛生與管理學院 醫學與社會發展研究中心 健康領域社會風險預測治理協同創新中心，重慶 400016;2.重慶市血液中心，重慶 400015)

近些年,隨著我國地市級醫院醫療服務水平的提高，罹患再生障礙性貧血、白血病、血小板減少性紫癜等血液病的城鄉居民，不再像以前不得不去省級綜合醫院接受治療，如今更多地選擇到中心血站覆蓋的地市級醫療機構就醫，致使地市級醫療機構血小板用量迅速增加，中心血站血小板供需矛盾突出，季節性和結構性血小板缺乏時有發生[1]。目前我國采供血機構尚無科學的臨床血小板需求預測方法，僅憑相關人員過往經驗簡單估算，實踐中時有血小板缺乏及過期報廢現象發生，本研究擬采用時間序列分析方法建立血小板臨床需求預測的自回歸移動平均(autoregressive integrated moving average，ARIMA)模型，為中心血站制定無償獻血招募及采集計劃提供科學依據。

1 資料與方法

1.1 數據來源

獲取2006至2016年重慶市6個中心血站每月向醫院提供的單采血小板臨床用量數據(單采血小板是用細胞分離機單采技術采集的血小板)。

1.2 ARIMA模型的建立

ARIMA模型建立的基本步驟：(1)時間序列分析及處理。對于平穩序列可直接擬合模型，非平穩序列需先進行平穩化處理。使用差分和季節差分分別對存在趨勢性和季節性的序列進行處理使其平穩。(2)模型識別與參數估計。根據自相關函數(autocorrelation function,ACF)圖和偏自相關函數(partial autocorrelation function，PACF)圖的特征，判斷其拖尾或截尾情況，初步確定p、q和P、Q值，提出幾種備選模型；對備選模型進行參數估計與假設檢驗，根據t檢驗結果中的P值進行判定，若P>0.05[2]則參數檢驗未通過；反之，則通過。然后依據貝葉斯信息準則(Bayesian information criterion，BIC)確定最佳模型。(3)模型檢驗。對模型的殘差序列進行白噪聲檢驗，主要是為了檢驗殘差是否存在自相關性，一方面可以根據殘差序列的自相關圖判斷，另一方面可以進行Ljung-Box Q檢驗。如果殘差序列不是白噪聲序列，則需進一步改進模型。(4)模型預測。運用最優模型預測2016年7至12 月每月血小板臨床需求量，計算95%置信水平下的置信區間以及相對誤差，以驗證模型的擬合效果。

1.3 統計學方法

運用Excel軟件建立數據庫，按月統計單采血小板臨床用量，以1個治療量計算；然后將其導入IBM SPSS Statistics軟件進行統計分析。

2 結果

2.1 單采血小板臨床用量時間序列分析及處理

繪制2006年1月至2016年6月每月單采血小板臨床用量的原始序列圖(圖1A)，可以看出原始序列存在明顯的上升趨勢，2006至2013年臨床用量逐年上升，2013至2016年上升趨勢才逐漸變緩。為了消除原序列趨勢性影響，故對其進行一階差分處理，結果見圖1B，可見原序列的上升趨勢不再明顯。

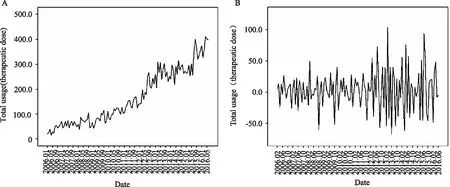
圖1 原始序列圖和經過一階差分后的序列圖

繪制原序列經過一階差分的自相關函數(ACF)和偏自相關函數(PACF)圖來檢驗原序列是否存在季節性，見圖2。由圖2可見，發現ACF和PACF在滯后12階均顯著不為0，表明原序列還存在季節周期性，以12個月為一個周期。因此，需要對原序列的一階差分序列進行季節差分，結果見圖3。從圖3可以看出經過一階差分和一階季節差分后序列中每個值都圍繞在固定值附近波動，為平穩序列。

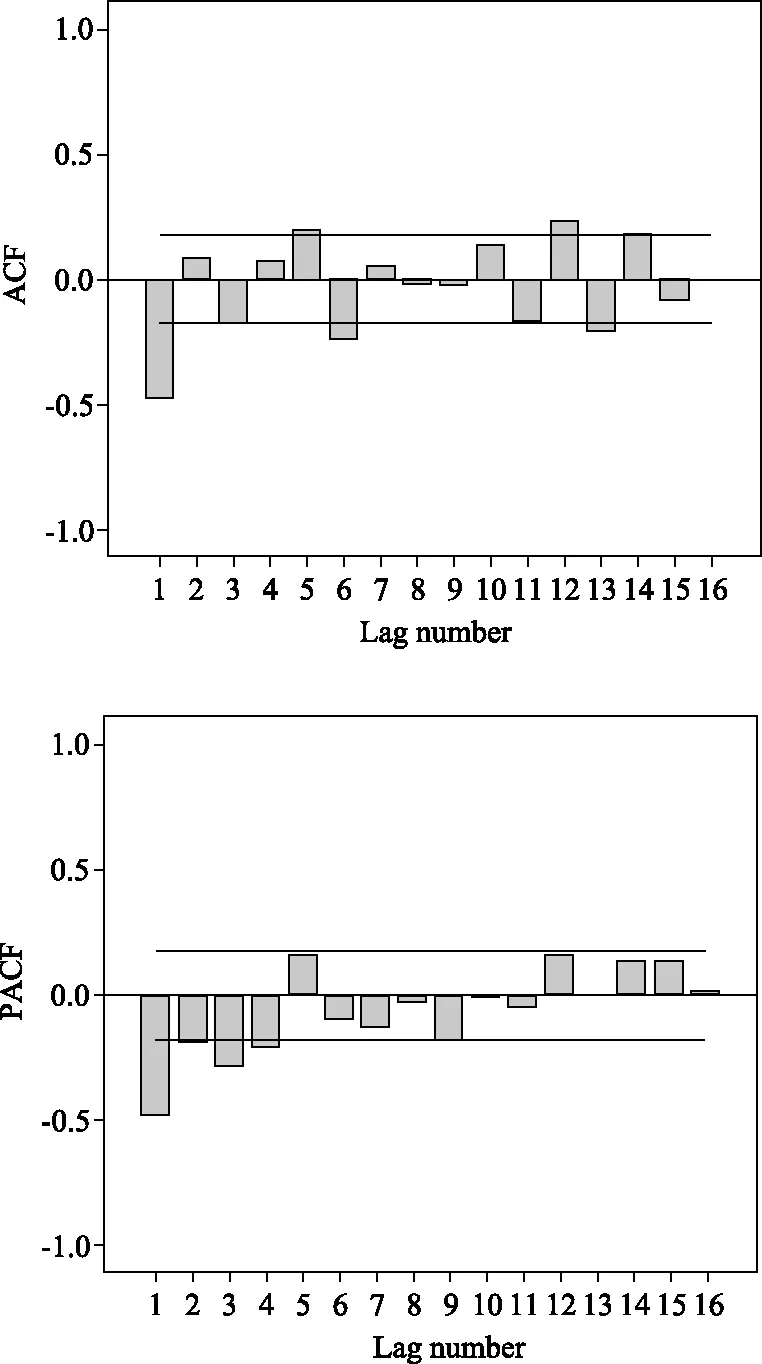
圖2 經過一階差分后的自相關函數和偏自相關函數圖

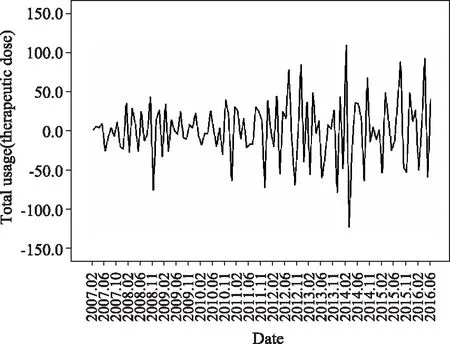
圖3 經過一階差分和一階季節差分后的序列圖

2.2 單采血小板臨床用量模型識別與參數估計

由于2006年1月至2016年6月每月單采血小板臨床用量序列存在明顯的趨勢性和季節性，故選用ARIMA乘積季節性模型，即ARIMA(p,d,q)(P,D,Q)s，其中p為非季節自回歸階數，d為非季節差分階數，q為非季節移動平均階數，P為季節自回歸階數，D為季節差分階數，Q為季節移動平均階數，s為季節長度。因序列的季節周期為12個月，故s取12；由于對原序列進行了一階差分和一階季節差分，因此d和D都取1。

繪制單采血小板臨床用量序列經過一階差分和一階季節差分序列的自相關函數(ACF)和偏自相關函數(PACF)圖，見圖4。圖4可見，ACF在滯后1、5、6、12、13階都有突出，表明ACF拖尾或者截尾特征不明顯，q取0；PACF在滯后1～5階突出，第5階后明顯收縮，因此判斷PACF呈5階截尾，p取5。同時，ACF在滯后12階顯著不為0，故Q取1；PACF在滯后12階可以認為是0，故P取0或1。綜上可知，識別模型為ARIMA(5,1,0)(0,1,1)12、ARIMA(5,1,0)(1,1,1)12。

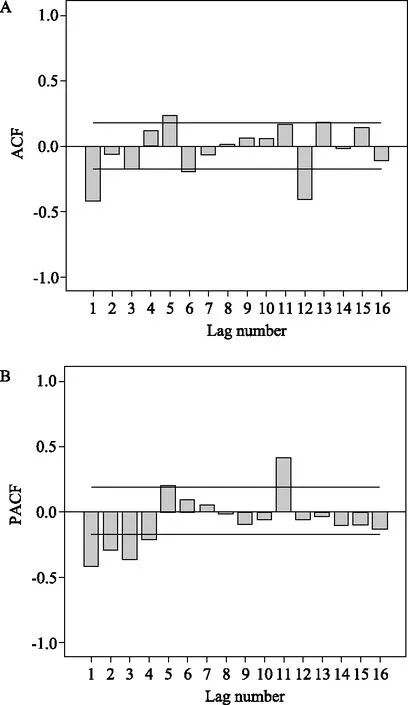
圖4 一階差分和一階季節差分后的自相關函數和偏自相關函數圖

識別模型的參數估計與假設檢驗見表1。從表1可知，識別模型ARIMA(5,1,0)(0,1,1)12和ARIMA(5,1,0)(1,1,1)12的參數顯著性檢驗均未通過(P>0.05)，故需重新選定模型。相關學者[3-4]認為P、D、Q三者取值一般不大于2，即取0、1或2；為了將模型考慮得更加全面，嘗試p和q取0的情況。采用從低階向高階不斷嘗試的辦法，通過比較各個模型的標準化BIC值，BIC值越小的模型，擬合效果越好[5-6]，最終選定最優模型為ARIMA(0,1,1)(1,0,1)12。

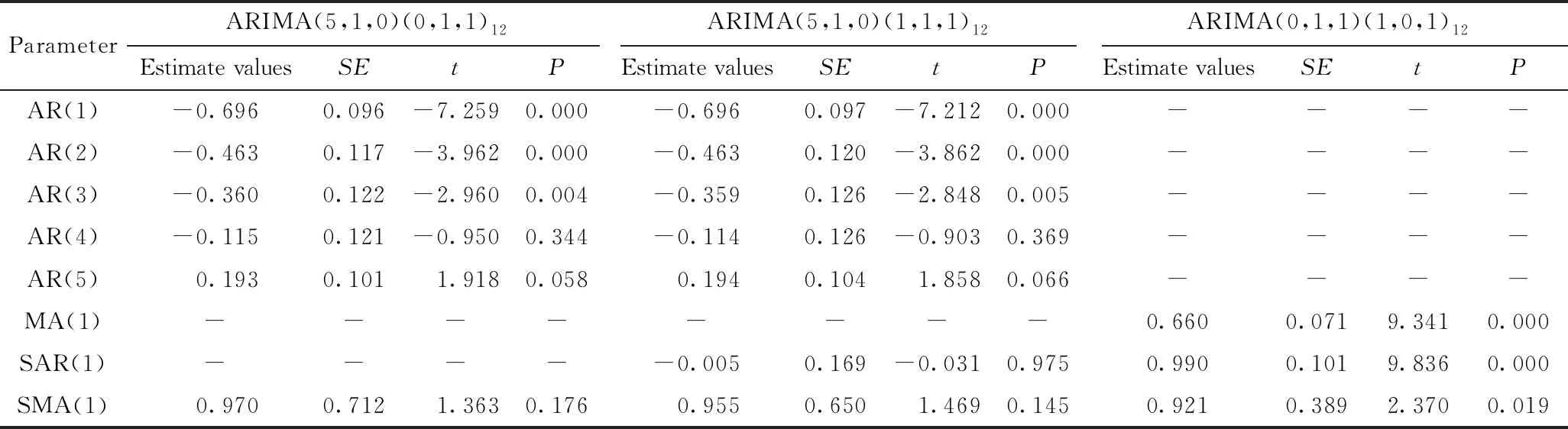
表1 識別模型和最優模型的參數估計值與假設檢驗

ARIMA: autoregressive integrated moving average;SE:standard error;AR： autoregressive;MA： moving average;SAR： seasonal autoregressive;SMA： seasonal moving average.

2.3 模型檢驗

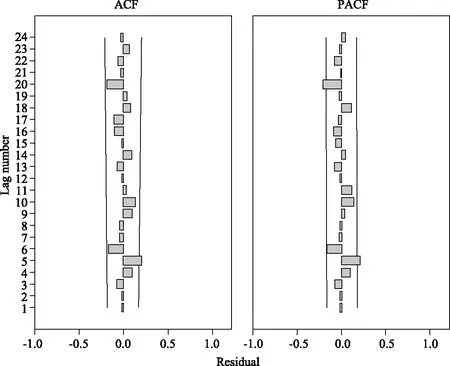
圖5 單采血小板臨床用量ARIMA(0,1,1)(1,0,1)12模型殘差序列自相關函數和偏自相關函數圖

對最優模型ARIMA(0,1,1)(1,0,1)12進行白噪聲診斷。由圖5可見，殘差序列自相關函數和偏自相關函數基本落在兩倍標準差范圍之內，即在95%的置信區間內；并且殘差序列Ljung-Box Q統計結果顯示P值大于0.05，表明殘差不存在相關關系。因此，模型ARIMA(0,1,1)(1,0,1)12的殘差序列滿足隨機性假設，為白噪聲序列，擬合模型顯著有效，適用于臨床單采血小板需求量的預測。

2.4 模型預測

應用最優模型ARIMA(0,1,1)(1,0,1)12預測2016年7-12月每月單采血小板臨床用量并評估模型的預測效果。預測結果顯示，實際值與預測值均在95%的置信區間內，平均相對誤差為7.5%(詳見表2)，模型擬合圖中預測值與實際值的曲線變化趨勢基本一致(圖6)。多數學者[7-9]認為平均相對誤差小于10%說明模型的預測結果精度較高，預測擬合效果好。

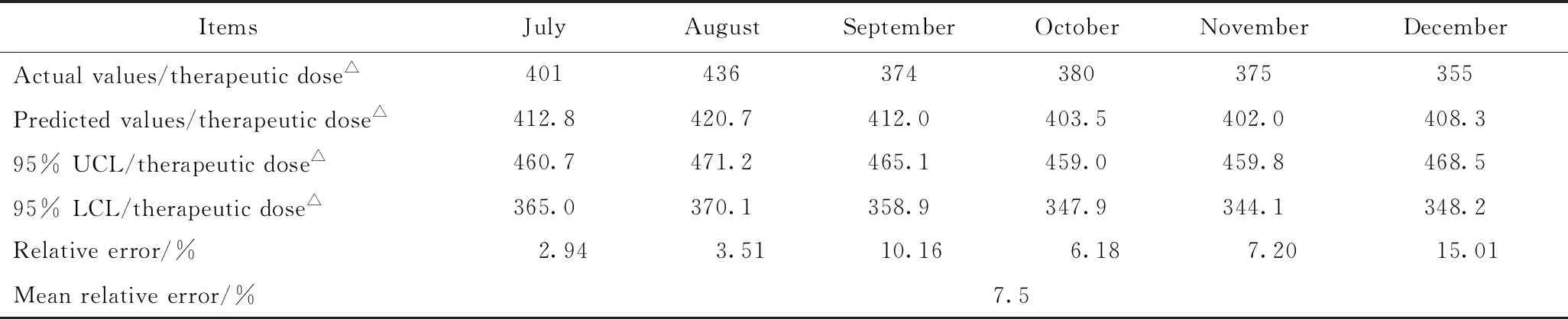
表2 2016年7至12月份每月單采血小板臨床用量預測值與實際值的比較

△: one therapeutic dose is 50 mL apheresis platelets;UCL: upper confidence limit;LCL: lower confidence limit.

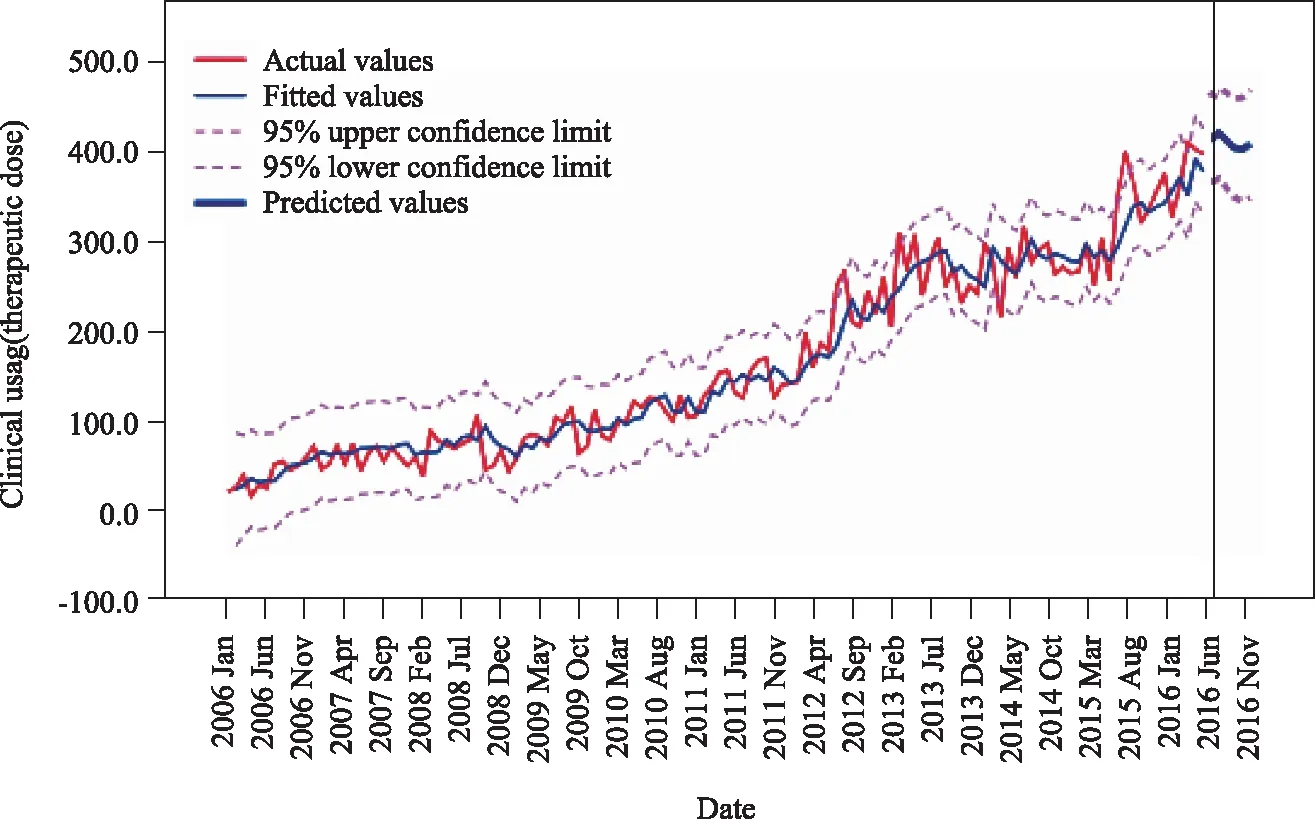
圖6 單采血小板臨床用量ARIMA(0,1,1)(1,0,1)12模型擬合效果圖

3 討論

時間序列預測是通過歷史數據來分析目標對象隨著時間而改變的內在規律，并利用外推機制將這種規律推演到未來，預測目標未來的變化情況，其中ARIMA模型是應用最廣泛的時間序列模型[10-11]。ARIMA模型通過不斷反復識別、修改和模型診斷，可篩選出最優的擬合預測模型，該模型具有適用性強和精確度高等特點，且能綜合分析線性趨勢、季節波動和隨機誤差等因素[12]，適用于與季節周期性相關的臨床血小板需求預測研究。

本研究將近些年血小板供需矛盾較為突出的中心血站納入研究視野，以重慶市中心血站為研究對象，利用中心血站2006年1月至2016年6月每月單采血小板臨床用量建立ARIMA模型，運用最終確定的最優模型對2016年7至12月每月單采血小板臨床需求量進行預測，預測結果顯示，平均相對誤差為7.5%，說明各模型的預測精度較高，擬合效果好。

臨床上血小板輸注主要用于治療血液病等各種因素所致的血小板數量下降或功能障礙。由于血小板的保存期限短，在溫度(22±2)℃的環境下保存時間小于5 d，建立血小板臨床需求量ARIMA預測模型，為血小板采集、制備、供給提供科學的依據，增強風險應對能力，使采供血機構提供的血小板量既能滿足臨床需求，又能避免過期浪費。有研究[13]表明ARIMA模型適宜短期(1年)預測，是由于ARIMA模型是依據歷史數據建立的預測模型，并未考慮政府相關政策出臺和調整、突發公共衛生事件等外部因素的影響[14-15]。因此，運用ARIMA模型預測血小板臨床用量時除需及時更新血小板臨床用量數據對模型類型、參數不斷完善[16]，以修正擬合效果最佳的模型以外，尚需關注外部因素可能帶來的影響。