基于深度學習的泊松散彈噪聲受限光子計數通信系統速率優化研究
胡思逸 沈岱靈 周小林 凌力


摘 要: ?泊松散彈噪聲具有非線性、非加性的性質,因而受到研究者的廣泛關注。20世紀80年代以來,大量關于泊松信道速率和容量的成果被提出。然而,由于泊松噪聲的特殊性質,導致速率公式復雜,過去的研究成果大多集中在理論極限性能的推導上下界的問題上。提出了一種基于深度學習的方法,針對復雜的速率公式,給出了非理想條件下的最優解,對于實際系統的性能有一定的參考價值。并且,深度學習較傳統梯度下降搜索算法有更高的泛用性和更快的速度。
關鍵詞: 泊松信道; 光子計數; 深度學習
中圖分類號: TP 311
文獻標志碼: A
Abstract: Poisson shot noise has the characteristics of non-linearity and non-additiveness, and has attracted widespread attention of researchers. Since the 1980s, a large number of results on Poisson channel rate and capacity have been proposed. However, due to the special nature of Poisson noise, the rate formula is complicated. Most of the previous research results have focused on the derivation of the theoretical limit performance. In this paper, a method based on deep learning is proposed. For the complex rate formula, the optimal solution under non-ideal conditions is given, which has certain reference value for the performance of the actual system. Moreover, deep learning has higher versatility and faster speed than traditional gradient descent search algorithms.
Key words: poisson channel; photon counting; deep learning
0 引言
在無線光通信系統中,接收端光子計數器產生的噪聲符合泊松分布,具有特殊的性質。在過去的研究中,泊松噪聲多被近似為高斯噪聲處理。然而,這一近似方法僅在光強較大時適用。近年來,許多學者嘗試針對泊松噪聲模型進行更精確的理論分析。Gong Chen研究了連續泊松信道速率模型下的功率分配[1]?,Verdu推導出了泊松速率公式的一些性質[2]。Amos Lapidoth在對離散泊松速率公式近似化簡的基礎上,推導了泊松信道速率的上界和下界[3]。然而,由于公式的復雜度較高,僅在發射功率較低時才有較好的近似效果,可用于研究系統的極限性能,但不易應用于針對實際系統的研究。而近年來廣泛應用的深度學習技術可研究復雜公式的性質,簡化了分析的難度,對于實際系統有一定的參考價值。
1 研究內容
1.1 泊松信道速率
采用光強調制/直接檢測(IM/DD)的單用戶無線光通信系統的結構,如圖1所示。
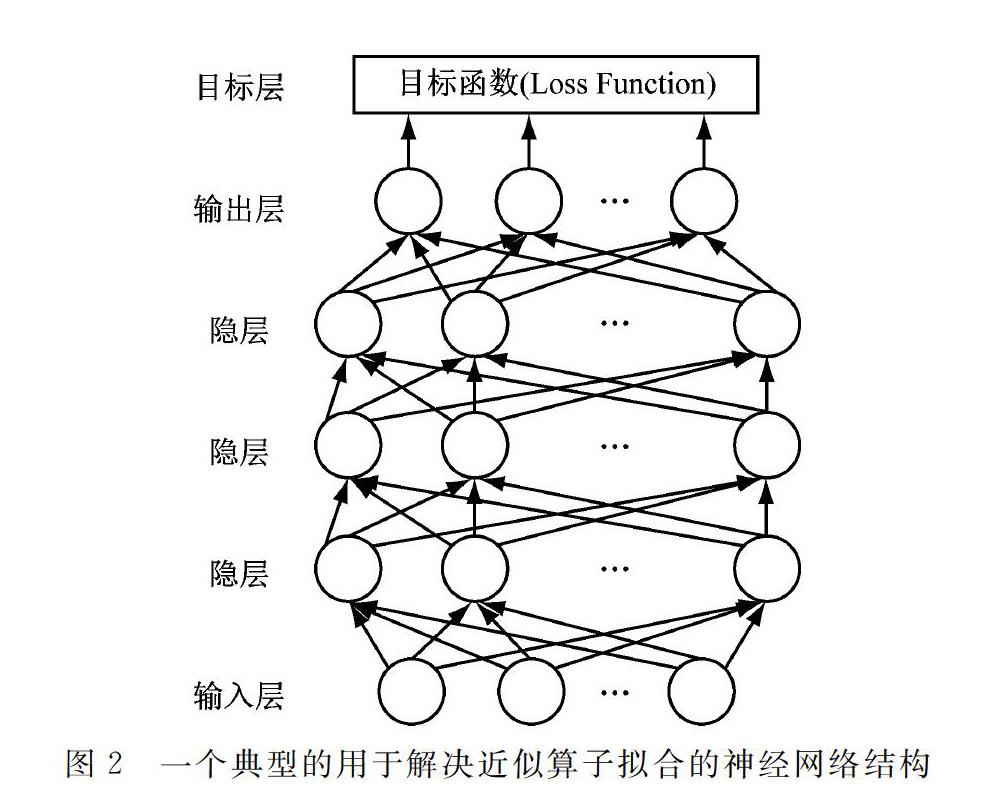
神經網絡作為多隱層的MLP,自然可以作為一個通用近似算子。神經網絡采用對目標函數(誤差函數)進行反向傳播與梯度下降的方法,實現對近似算子的擬合。這種擬合在一類不具備結構化公式的問題以及在一類復雜的結構化公式的最優解問題上得到了較為廣泛的應用[8-9]。
1.3 優化算法設計
本文聚焦于多信道的泊松噪聲下用戶功率的優化問題,采用深度學習的方法,對傳統復雜問題的最優解進行梯度下降形式的搜索工作。本文所建立的模型具有傳統方法不具備的優勢:
1、傳統的數學方法使用求偏導的方式對高復雜度的數學公式進行梯度的計算和迭代來求取最優解,效率較低且易陷入局部最優。
2、神經網絡在沒有離散標簽的情況下,無法有效進行離散形式的輸出。
算法的主要改進有兩點。第一,采用特殊構造的輸入對網絡的收斂方向進行控制。純隨機的變量輸入會導致網絡的輸出的不穩定,由于本文所構建的目標函數的級數較大(近似為有限階乘),訓練過程中易造成梯度爆炸。第二,目標函數需要離散值作為輸入。由于梯度只能保存在連續的變量中,離散的輸出值會導致梯度消失。算法的具體細節如表1所示。
算法采用保存對連續變量近似到最近離散值(自然數)的方法,將去除梯度的近似距離作為加函數疊加到原始輸出值上,解決梯度消失問題。算法中Nb代表背景光子數組合,Rate代表分配的發射光子數組合,model代表神經網絡,I代表目標函數,具體參見公式(3)、(4)。
2 仿真和分析
2.1 仿真設置
本文中使用的實驗平臺為Windows10操作系統,硬件環境為2核Intel(R) Core(TM) i5-7500 CPU @ 3.40 GHz,內存為24 GB,顯卡為NVIDA的 GTX 1060,顯存為6 G。本實驗模型實驗均在Pytorch環境下搭建。
本文采用的實驗數據根據1.1節所介紹,由于不同頻率的光同時發送信息,大氣中的背景光會對其形成干擾,而不同頻率的光子在大氣中的數量不同。本文根據不同的環境條件,共進行3組實驗,環境參數設置分別為:
其中,batch_size代表參與一次梯度下降的批次大小,前兩組由于輸入固定,為了符合神經網絡并行計算的要求,batch_size的值大于等于2;第三組由于求取泛化的最優解,故設置batch_size為100。K代表信道數。Rc與R為常量。ns_ave 代表網絡輸出上增加的手動偏移,由于默認背景光總數為40*信道數,故設置網絡的初始搜索點為40+初始的網絡輸出值。ns_total代表信道的背景光總數。采用的優化器為adam,學習速率為0.001,訓練總次數設置為50個迭代。
由于信道數在3,4的情況下,可以用遍歷的方法得到函數的最優解,故本文采用組一組二兩組來驗證模型最優解的可行性。信道數較高情況下(>=10),使用遍歷的方法得到函數最優解的計算代價過大,神經網絡的泛化性使得模型在不同輸入情況下,可以產生泛化的目標輸出,以此減小傳統方法的計算資源浪費,故采用實驗組三的參數,來驗證預訓練的模型可以在不同背景光子參數輸入下得到不同最優解,達到模型泛化與效率提升。
2.2 實驗結果與實驗分析
如圖3所示。
三信道與四信道實驗結果可見,模型所采取的使用近似距離來保存梯度的方法,對于網絡的訓練是有效的。模型在40-50個epoch時收斂于最優值附近。
模型的輸入分別為5,5,50(三信道)與5,5,5,50(四信道)。由遍歷法可得,最優解為37,37,46(三信道)與38,38,38,46(四信道),與模型收斂值曲線的最高點所在信道功率相同。如圖4所示。
根據實驗所產生的結果模型在每個epoch隨機生成10個背景光子組合進行了評估并記錄所有性能的均值,最后,展示了性能的變化折線。由曲線可見,模型在隨機產生的背景光子組合下的性能逐步提升,最終收斂在9.42附近,證明在不同的背景光子下,模型產生的最優解產生了足夠強的泛化性,使得和速率輸出穩定。
2.3 優化性能分析
將訓練好后的模型應用于實際場景中,隨機選取一組背景光子Nb,選取不同信道數場景,比較均勻功率下的性能和經過優化后的系統性能,如圖6所示。
由圖6分析可得,經過訓練后的模型,在10信道與30信道的情景下,在不同的背景光子總數下,優化算法對系統的性能都具有明顯的提升。其中在10信道下,優化算法對和速率的提升隨著發射光子總數的增大基本穩定,而在30信道下,和速率提升隨著發射光子總數的增大而逐漸增大,這說明在信道數較高且發射總光子數較大的情況下,優化算法對和速率的提升更加明顯。
3 總結
本文使用深度學習的方法對泊松單用戶并行信道的優化進行了研究,針對搜索離散變量最優解的問題,對算法做出了一定的改進。由仿真結果可知,對于泊松散彈噪聲受限光子計數問題,深度學習可通過梯度下降的方法進行離散最優點搜索,這種方法為解決泊松優化問題提供了一種新的思路。仿真結果顯示,算法在不同的信道數與不同總光子數條件下均可得出最優解,并具有較強的泛化性。
參考文獻
[1] Liu B, Gong C, Cheng J, et al. Power Allocation Over Broad Spectra Optical Wireless Scattering Communication Based on Link Gain Correlation[J]. IEEE Transactions on Communications, 2019, 67(10): 6980-6993.
[2] Guo D, Shamai S, Verdú S. Mutual information and conditional mean estimation in Poisson channels[J]. IEEE Transactions on Information Theory, 2008, 54(5): 1837-1849.
[3] Lapidoth A, Shapiro J H, Venkatesan V, et al. The discrete-time Poisson channel at low input powers[J]. IEEE Transactions on Information Theory, 2011, 57(6): 3260-3272.
[4] Bashbaghi S, Granger E, Sabourin R, et al. Deep Learning Architectures for Face Recognition in Video Surveillance[J]. 2019: 133-154.
[5] Bengio Y. Learning Deep Architectures for AI[J]. Foundations & Trends? in Machine Learning, 2(1):1-127.
[6] I Goodfellow, Y Bengio, A Courville. Deep learning[M]. Cambridge: MIT Press, 2016.
[7] Schmidhuber, Jürgen. Deep learning in neural networks: An overview[J]. Neural Network, 2015(61):85-117.
[8] Alex Krizhevsky, I Sutskever, G Hinton. ImageNet Classification with Deep Convolutional Neural Networks[J]. Advances in neural information processing systems, 2012, 25(2):1097-1105.
[9] Graves A, Mohamed A R, Hinton G. Speech Recognition with Deep Recurrent Neural Networks[J].2013(5):6645-6649.
(收稿日期: 2019.08.11)

