關(guān)于方程 Z（n）=φe（SL（n））的正整數(shù)解

朱 杰，廖群英

（四川師范大學數(shù)學科學學院，四川成都610066）

1 引言及主要結(jié)果

關(guān)于數(shù)論函數(shù)方程的研究是數(shù)論中十分重要和有意義的課題，其中涉及很多重要的函數(shù)，例如廣義歐拉函數(shù)、偽Smarandache函數(shù)和Smarandache LCM函數(shù).18世紀杰出數(shù)學家歐拉提出了著名的歐拉函數(shù)，正整數(shù)n的歐拉函數(shù)φ（n）定義為序列1，2，…，n-1 中與 n 互素的整數(shù)個數(shù)[1].20 世紀70年代，該函數(shù)在RSA公鑰密碼體制中扮演著重要角色.2007年，Cai等[2]在歐拉函數(shù)的基礎(chǔ)上提出了廣義歐拉函數(shù)的概念.對任意的正整數(shù)e，正整數(shù)n的廣義歐拉函數(shù) φe（n）定義為序列1，2，…，中與n互素的數(shù)的個數(shù)，即

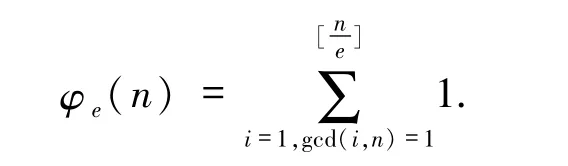
由廣義歐拉函數(shù)的定義易知；當 e=1時，有φ1（n）=φ（n），即著名的歐拉函數(shù)；當 e=2 時，有后來蔡天新等[3]和沈忠燕等[4]給出了 φe（n）（e=3，4，6）的準確計算公式.最近，文獻[5-6]給出了一類特殊正整數(shù)的廣義歐拉函數(shù)e∈｛pt，pq｝的計算公式，其中p、q為不同的素數(shù)，t為正整數(shù).

另一方面，著名數(shù)論專家Smarandache定義了正整數(shù)n的Smarandache函數(shù)，后來人們在Smarandache函數(shù)的基礎(chǔ)上，定義了正整數(shù)的偽Smarandache函數(shù)和Smarandache LCM函數(shù).文獻[7]證明對任意的正整數(shù)n，偽Smarandache函數(shù)Z（n）定義為使得1+2+…+m能被n整除的最小正整數(shù)m，即

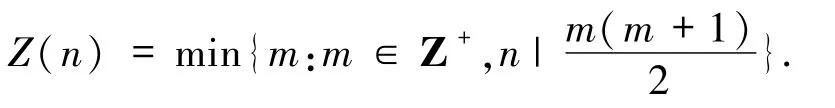
對任意的正整數(shù) n，Smarandache LCM函數(shù)SL（n）定義為最小的正整數(shù) m，使得 1，2，…，m 的最小公倍數(shù)能被 n整除[8]，即

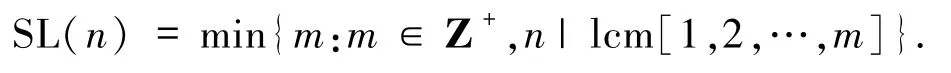
近年來，一些學者研究了這3類函數(shù)的性質(zhì)及相關(guān)方程，例如：范盼紅[9]利用初等方法對此問題進行了研究，給出了方程Z（n）=φ（n）的解的所有形式；魯偉陽[10]研究了 Z（n2）=φ（n）的所有正整數(shù)解的問題；趙艷琳[11]完全確定方程SL（n）=φ（n）的正整數(shù)解.

最近，朱杰等[12]討論了 e∈｛1，2，3，4，6｝時，方程

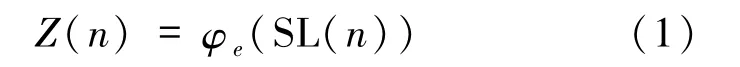
的可解性.本文繼續(xù)該問題研究，推廣了文獻[12]的結(jié)果，討論了 e∈｛pt，pq｝時，方程（1）的可解性，其中p、q是不同的素數(shù)，t為正整數(shù).事實上，給出了 e∈｛pt，pq｝時，方程（1）沒有正整數(shù)解的幾個充分條件，即證明了如下主要結(jié)果.

定理1.1設(shè) p，p1，p2，…，pk為不同的素數(shù)，t為正整數(shù)，α，α1，α2，…，αk≥0，則方程（1）沒有滿足如下條件的n值：

1）e=pt（t≤2）且

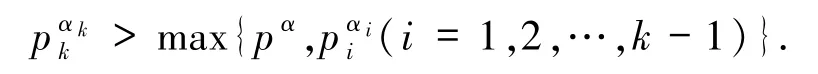
2）e=pt（t≥3）且，其中.

定理1.2設(shè) p、q、p1、p2、…、pk為不同的素數(shù)，α，β，α1，α2，…，αk≥0，e=pq.若

則方程（1）沒有滿足如下條件的n值：

2 相關(guān)引理

為方便，記Ω（n）為n的素因子個數(shù)（重復計數(shù)），ω（n）為 n的不同的素因子個數(shù)，即，規(guī)定 Ω（1）=ω（1）=0，并記gcd（a，b）表示整數(shù)a和b的最大公因數(shù).為證明本文的主要結(jié)果，需要如下幾個引理.

引理2.1[13]設(shè)正整數(shù)n的標準分解式為，則

特別地，對任意素數(shù) p及正整數(shù) α，有SL（pα）=pα.

引理2.2[5]若，其中α≥0，αi＞0，p、pi（1≤i≤k）是不同的素數(shù)，則

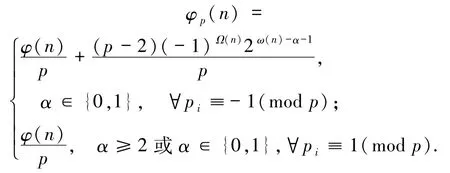
引理2.3[5]設(shè) n=pαn1＞ p2，其中，且 p、pi（1≤i≤k）是不同的素數(shù)，則

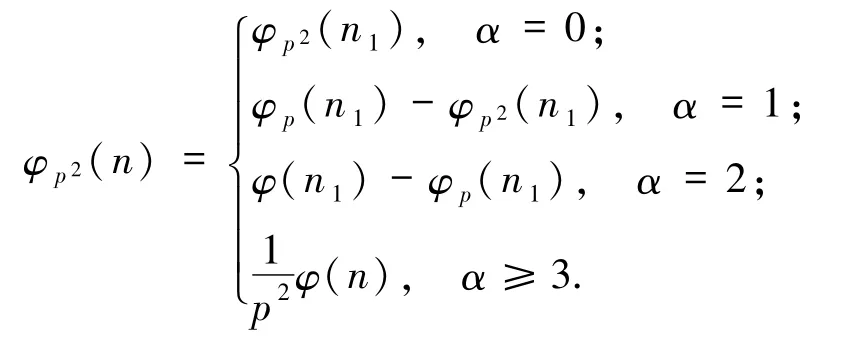
特別地，當α=0時有

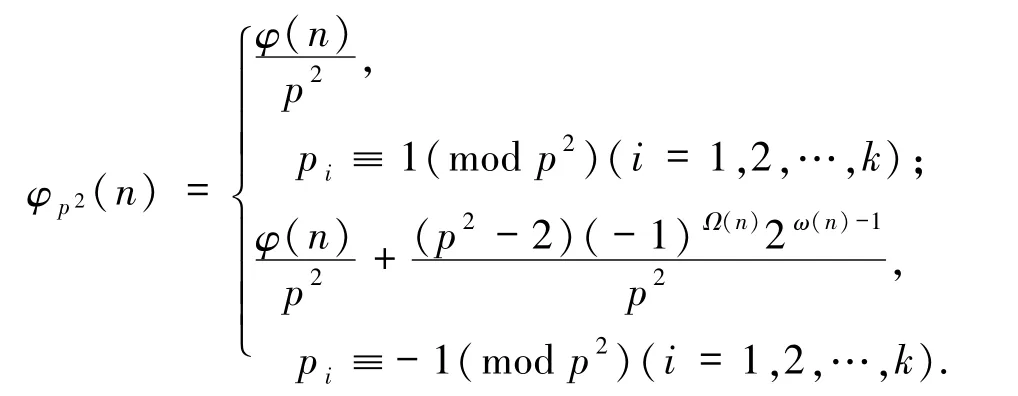
引理2.4[6]設(shè) p、pi（1≤i≤k）是不同的素數(shù)，則

定理2.5[5]設(shè)，其中 α，β≥0，αi＞0，且 p、q、pi（1≤i≤k）是不同的素數(shù).

1）若α≥2且β=0，則

2）若 α∈｛0，1｝且 β≥2，則

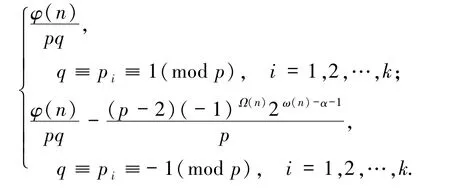
3）若α=β=0，則

3 主要結(jié)果的證明

定理1.1 的證明1）當 e=pt（t≤2）時，設(shè)，其中 p，p1，p2，…，pk為不同的素數(shù)，α，α1，α2，…，αk≥0.

（a）若 t=1，即 e=p，此時方程（1）即為Z（n）=φp（SL（n））.

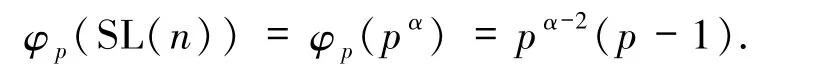
若 Z（n）=φp（SL（n）），則由 Z（n）的定義得

故

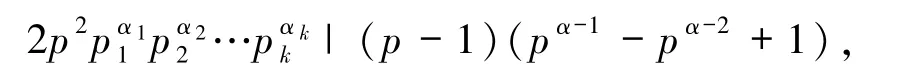
從而

故 p｜（p-1）（pα-1-pα-2+1）.又 gcd（p，p-1）=1，故 p｜（pα-1-pα-2+1），即 p｜（1-pα-2），從而α =2.此時由（2）式得 p2｜（p-1）p，即 p｜（p-1），顯然矛盾.

（i）若 pk≡1（mod p），則由引理2.2 得

若 Z（n）=φp（SL（n）），則由 Z（n）的定義得

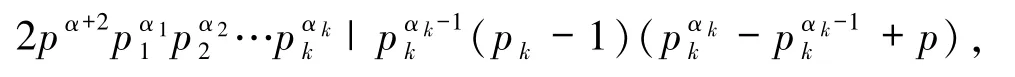
（ii）若 pk≡ -1（mod p），則由引理2.2 得

若 Z（n）=φp（SL（n）），則由 Z（n）的定義得

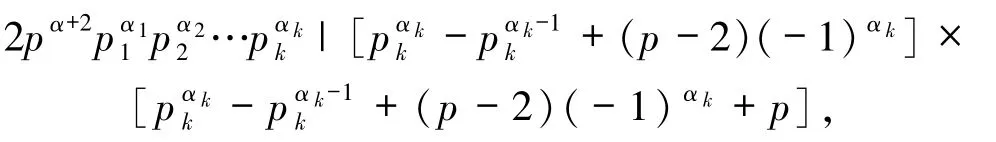
特別地，

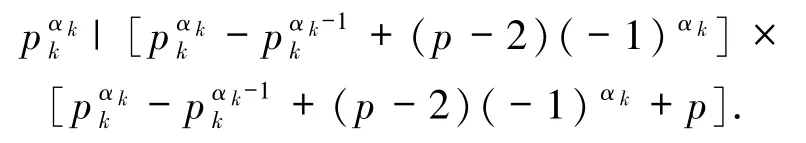
若

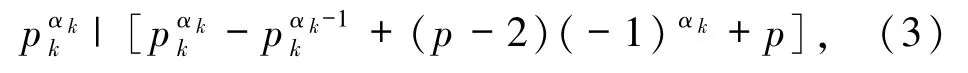
則

當 αk＞1 且為偶數(shù)時，由（4）式得 pk｜2（p-1），故pk=2 或 pk｜（p-1）.若 pk=2，則由 pk≡ -1（mod p）可知 p=3.此時由（3）式得 2αk｜（2αk-1+4），故 αk=3，此與 αk為偶數(shù)矛盾.故 pk｜（p-1），則 pk≤p-1.又 pk≡ -1（mod p），故 pk≥p-1，進而 pk=p-1，故由 p、pk為素數(shù)可得 p=3，pk=2，仍然矛盾.故αk＞1且為奇數(shù)，由（4）式得 pk=2，再由 pk≡ -1（mod p）知 p=3.此時由（3）式得 2αk｜（2αk-1+2），故 αk=2，此與 αk為奇數(shù)矛盾.故 αk=1，此時由（4）式得 pk｜1，顯然矛盾.

若存在 r（1≤r＜ αk），使得

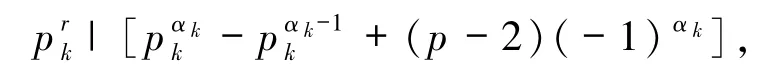
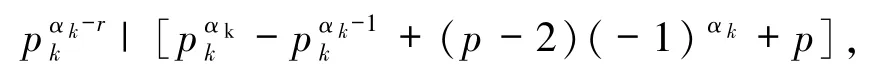
由以上證明知此種情況不成立.

（b）若 t=2，則 e=p2，此時方程（1）即為Z（n）=φp2（SL（n））.

顯然 Z（n）≠0.當 α =2時，有 φp2（SL（n））=φp2（p2）=1，顯然 Z（n）≠1.故 α≥3，此時由引理2.3得

若 Z（n）=φp2（SL（n）），則由 Z（n）的定義得

從而

故 p｜（p-1）（pα-2-pα-3+1）.又 gcd（p，p-1）=1，故 p｜（pα-2-pα-3+1），即 p｜（1-pα-3），從而α =3.此時由（5）式得 p3｜（p-1）p，即 p2｜（p-1），顯然矛盾.

（i）若 pk≡1（mod p2），則由引理2.3 得

若 Z（n）=φp2（SL（n）），則由 Z（n）的定義得

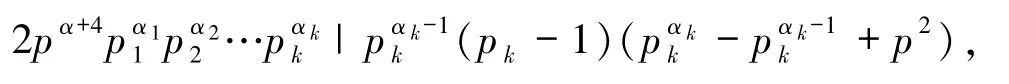
（ii）若 pk≡ -1（mod p2），則由引理2.3 得

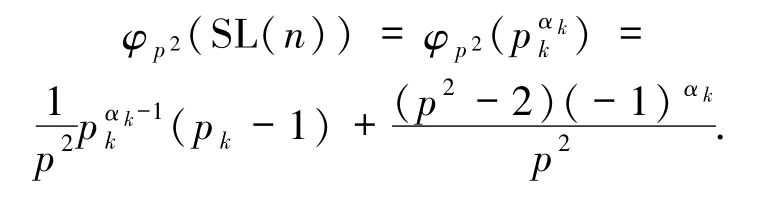
若 Z（n）=φp2（SL（n）），則由 Z（n）的定義得

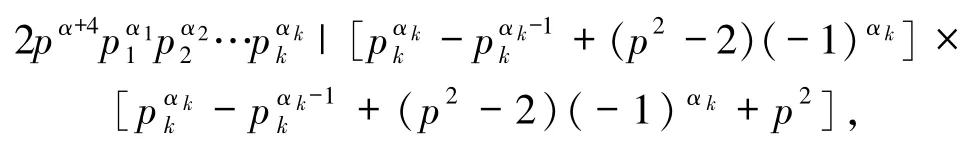
特別地，

若

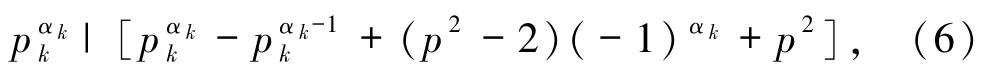
則

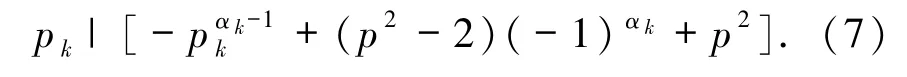
當 αk＞1 且為偶數(shù)時，由（7）式得 pk｜2（p2-1），故 pk=2 或 pk｜（p2-1）.若 pk=2，則由 pk≡ -1（mod p2）知 p2=3，顯然矛盾.故 pk｜（p2-1），則 pk≤p2-1.又 pk≡ -1（mod p2），故 pk≥p2-1，進而 pk=p2-1，故由 p、pk為素數(shù)可得 p=2，pk=3，此時再由（6）式可得3αk｜（2·3αk-1+6），顯然不成立.故 αk＞1且為奇數(shù).因此，由（7）式得 pk=2，再由 pk≡ -1（mod p2）知 p2=3，顯然矛盾.故 αk=1，此時由（7）式可得 pk｜1，顯然矛盾.

若存在 r（1≤r＜ αk），使得

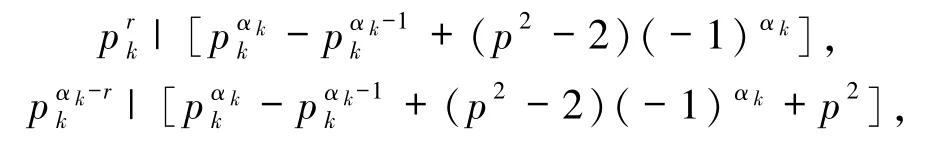
由以上證明知此種情況不成立.

2）當 e=pt（t≥3）時，其中 t為正整數(shù)，此時方程（1）即為 Z（n）=φpt（SL（n））.現(xiàn)設(shè)

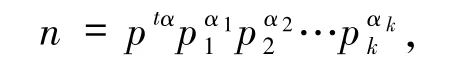
其中 p、p1、p2、…、pk為不同的素數(shù)，α，α1，α2，…，αk≥0.

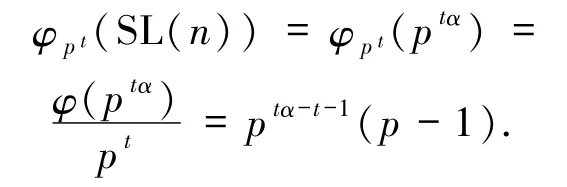
若 Z（n）=φpt（SL（n）），則由 Z（n）的定義得

從而

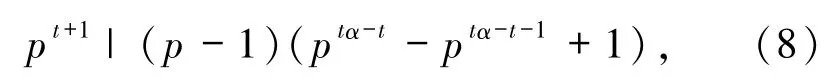
故 p｜（p-1）（ptα-t-ptα-t-1+1）.又 gcd（p，p-1）=1，故 p｜（ptα-t-ptα-t-1+1），即 p｜（1-ptα-t-1），從而tα =t+1.此時由（8）式得 ptα｜（p-1）p，顯然矛盾.

這就完成了定理1.1的證明.

定理1.2的證明當e=pq時，此時方程（1）即為 Z（n）=φpq（SL（n））.現(xiàn)設(shè)，其中 p，q，p1，p2，…，pk為不同的素數(shù)，α，β，α1，α2，…，αk≥0.

（I）若 p≡1（mod q），則由引理2.5 的1）得

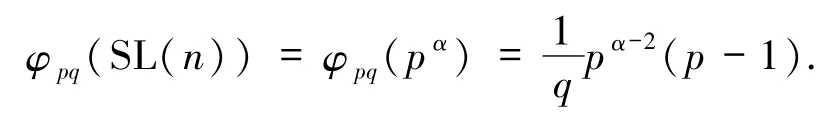
若 Z（n）=φpq（SL（n）），則由 Z（n）的定義得

從而 p2｜（p-1）（pα-1-pα-2+q），故 p｜（p-1）（pα-1-pα-2+q）.又 gcd（p，p-1）=1，故 p｜（pα-1-pα-2+q），即 p｜（q-pα-2），從而 α =2 且 p｜（q-1），故 p≤q-1.又 p≡1（mod q），故 p≥q+1，顯然矛盾.

（II）若 p≡ -1（mod q），則由引理2.5 的1）得

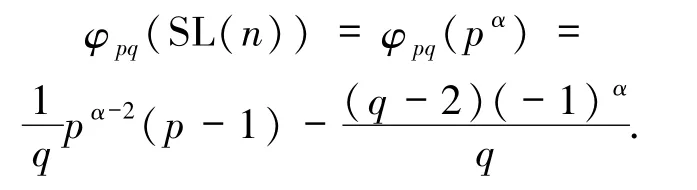
若 Z（n）=φpq（SL（n）），則由 Z（n）的定義得

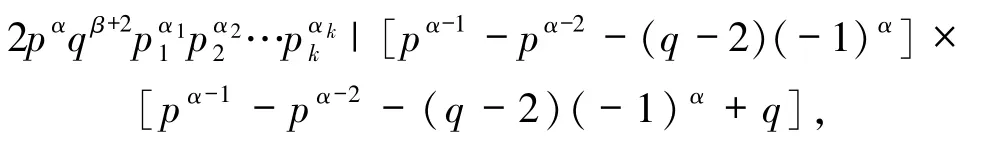
從而

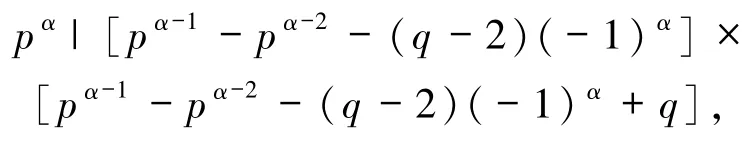
若 pα｜[pα-1-pα-2- （q-2）（-1）α]，則 p｜[-pα-2-（q-2）（-1）α].當 α ＞2 時，有 p｜（q-2），故 p≤q-2.又 p≡ -1（mod q），故 p≥q-1，顯然矛盾.從而 α =2，此時得 p｜（q-1），故 p≤q-1.又 p≡ -1（mod q），故 p≥q-1，進而 α =2 且 p=q-1.由p，q為素數(shù)可得 p=2，q=3.注意到22=pα＞max｛3β，故 n=4 或 n=4×3.若 n=4，φ6（SL（4））=φ6（4）=0，顯然Z（4）≠0.若 n=12，又 12=4 ×3，由引理2.1 得SL（12）=4，故 φ6（SL（12））=φ6（4）=0，顯然Z（12）≠0.

若

則

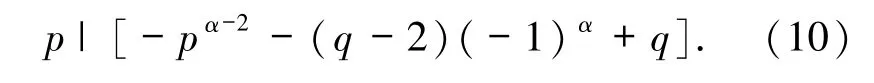
當α＞2且為偶數(shù)時，由（10）式可得p=2，再由p≡-1（mod q）可知 q=3.此時由（9）式可得2α｜（2α-2+2），顯然不成立.故α＞2且為奇數(shù)，由（10）式可得p｜2（q-1），故 p=2 或 p｜（q-1）.若 p=2，則由 p≡-1（mod q）可知 q=3.此時由（9）式得2α｜（2α-2+4），顯然不成立.故 p｜（q-1），則 p≤q-1.又 p≡-1（mod q），故 p≥q-1，進而 p=q-1，故由 p、q 為素數(shù)可得p=2，q=3，仍然矛盾.故 α=2，此時由（10）式得 p｜1，顯然矛盾.

若存在 r（1≤r＜ α），使得

由以上證明知此種情況不成立.

（I）若 pk≡1（mod pq），則由引理2.5 的 3）得

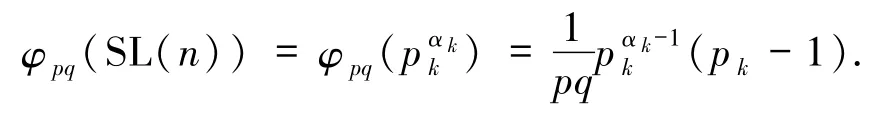
若 Z（n）=φp（SL（n）），則由 Z（n）的定義得

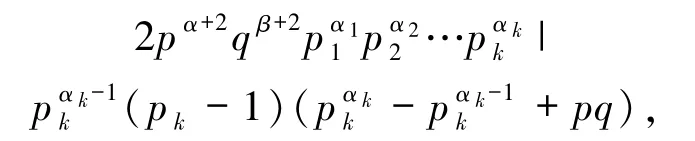
（II）若pk≡ -1（mod pq），則由引理2.5 的3）得

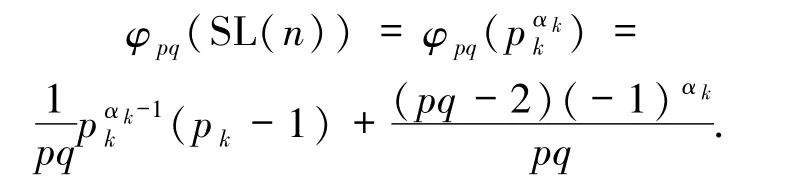
若 Z（n）=φpq（SL（n）），則由 Z（n）的定義得

特別地，

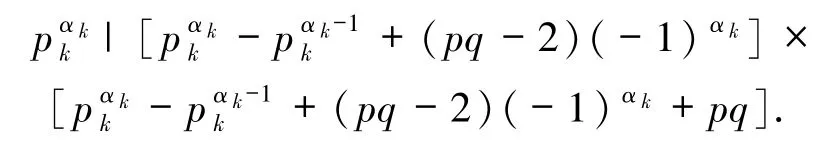
若

則

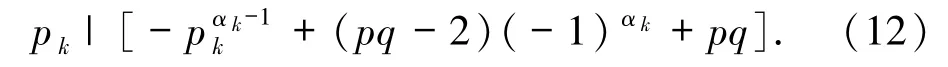
當 αk＞1 且為偶數(shù)時，由（12）式得 pk｜2（pq-1），故 pk=2 或 pk｜（pq-1）.若 pk=2，則由 pk≡ -1（mod pq）可知 pq=3，顯然矛盾.故 pk｜（pq-1），則pk≤pq-1.又 pk≡ -1（mod pq），故 pk≥pq-1，進而 pk=pq-1.此時，再由（11）式可得，若 αk=2，則 pk｜（pk+1），顯然不成立.故 αk≥3 且 pk=2，即 2αk｜（2αk-1+4），得 αk=3，此與 αk為偶數(shù)矛盾.故 αk＞1且為奇數(shù)，由（12）式得 pk=2，再由 pk≡ -1（mod pq）可知 pq=3，顯然矛盾.故 αk=1，此時由（12）式得 pk｜1，顯然矛盾.

若存在 r（1≤r＜αk），使得

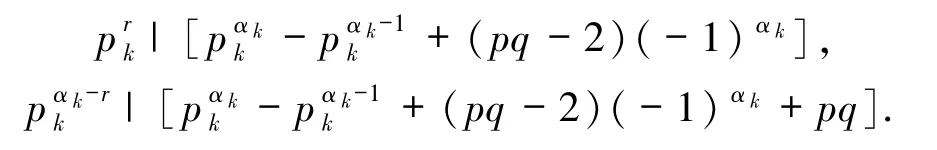
由以上證明知此種情況不成立.這就完成了定理1.2的證明.

4 應用舉例

本節(jié)通過實例進一步驗證定理1.1～1.2，其中例4.1對應定理1.1，例4.2對應定理1.2.

例4.1取e=5，n=25，31或29.

若n=31，由31是素數(shù)，從而由Z（n）的定義知Z（31）=30，又由SL（n）的定義知SL（31）=31，故φ5（SL（31））=φ5（31）.又中與31互素的數(shù)的個數(shù)為6，故 φ5（31）=6，故 Z（31）≠φ5（SL（31））.若 n=29，同理可得 Z（29）≠φ5（SL（29））.

例4.2取 e=14，n=49，43 或41.

若n=43，由43是素數(shù)，從而由Z（n）的定義知Z（43）=42，又由SL（n）的定義知SL（43）=43，故φ14（SL（43））=φ14（43）.又中與43互素的數(shù)的個數(shù)為3，故φ14（43）=3，故 Z（43）≠φ14（SL（43））.若 n=41，同理可得 Z（41）≠φ14（SL（41））.

由上面的例子可以看出，當 n值滿足定理1.1～1.2的條件時，此時方程（1）無該類解.

5 進一步的結(jié)果

前面給出了p、q為不同的素數(shù)，t為正整數(shù)，且e∈｛pt，pq｝時，方程（1）沒有正整數(shù)解的幾個充分條件.通過實例也發(fā)現(xiàn)當e為pt，pq這些特殊值時，該方程在很多情況下都沒有正整數(shù)解.本節(jié)利用φe（pα）（α≥1）的計算公式，進一步討論方程（1）的可解性.

對任意素數(shù)p，以及任意正整數(shù)α、e，由廣義歐拉函數(shù)的定義可知

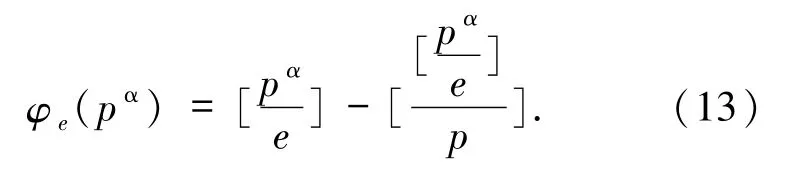
由此可得：

定理5.1方程（1）的全部正整數(shù)解為e=1，n=1 或，其中 p，q1，q2，…，qs為不同的素數(shù)，α1，α2，…，αs≥0，且

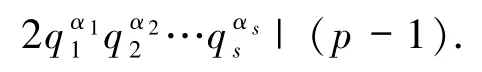
證明若n=1時由定義知Z（1）=SL（1）=1，此時方程（1）即為 φe（1）=1，故 e=1.

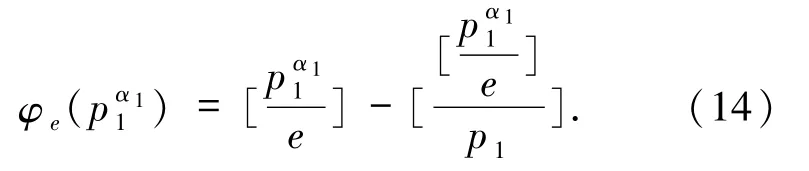
因此，由方程（1）可得

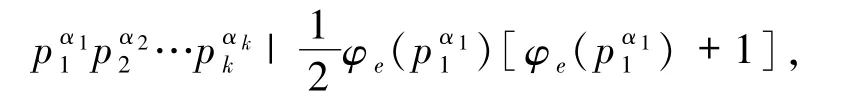
從而

由于（φe（p1），φe（p1）+1）=1，則由（15）式可得因?qū)θ我庹麛?shù)但由e≥2 以及（14）式知，矛盾.故 e=1，從而.又，故 α1=1，即，且，即，其中定理5.1 得證.