關于梯形有關概念教材編寫及二次開發研究（二）

劉憲升

[摘要]簡單梳理“梯形”作為數學名詞的來源，并借助梯子的結構，分析了梯形是對其結構（空間）形式和數量關系的本質屬性抽象提煉的結果，是人們大腦的反映，展現了梯形有關概念的來源及合理性，水到渠成地得到了梯形的中位線定理，給出了教學中應實現數學知識與生活的有機融合和重視民族語言保護的建議。

[關鍵詞]梯形;梯子;概念;生活

[中圖分類號]

G623.5

[文獻標識碼]A

[文章編號] 1007-9068（ 2020）20-0006-03

研究（一）中提到，現行教材中梯形概念的探索活動大多注重與生活的聯系，可沒有真正觸及梯形有關概念來源于生活的本質。那是不是真的可以從生活中抽象、提煉出這種圖形為什么叫梯形，為什么只有一組對邊平行，為什么上底比下底短等相關知識呢？答案是肯定的。本文就對此做一探討。

一、數學中“梯形”一詞的來源

數學中的梯形在我國古代的數學文獻中早已出現，且能計算它的面積，但不是現今的稱呼。我國古代數學重視實用，梯形及其面積的求法就是應丈量田地的需要而誕生的。

《九章算術》“方田”章中有“邪田”“箕田”的度量術。其中，“邪田”即斜田，就是現今直角梯形形狀的田地;“箕田”就是現今等腰梯形形狀的田地。梯形的兩底稱為舌、踵，高稱為正從。但沒有出現一般梯形田地的度量，可能是因為它能分成兩個直角梯形形狀田地的緣故。《五曹算經》中，在繼承《九章算術》的基礎上又增加了“簫田”的算法，和“邪田”“箕田”并存且算法相同。這里的“簫田”就是一般的梯形（不是等腰梯形和直角梯形）田地。雖然書中未做解釋，但因為古代的簫是多管的，形狀像鳥翼，鳥翼兩側（相當于梯形兩腰）是斜（不與梯形的底垂直）的且不相等，故“簫田”就是指形狀像一般梯形的田地。

在徐光啟翻譯的《幾何原本》卷一（四庫全書本）中沒有“梯形”這個名字，它被歸入無法四邊形之中。根據法國傳教士張誠、白晉從法文譯本修訂的，收錄于《御制數理精蘊》上篇卷二中的《幾何原本》（四庫全書本）中也沒有“梯形”，且據其四邊形的分類看不出屬于哪一類。

清朝柘城杜知耕撰寫的《數學鑰》卷一（四庫全書本）（http：//www.kanripo.org/text/KR3f0050/001）關于四邊形的分類如下：

四速皆等四角中矩者日方形如第一固四角中矩四邊雨雨相等者日直形如第二固或四速等或雨速等而四角俱不中矩者日象目形如第三國四速俱不等雨角中矩雨角不中矩者日斜方形如第四固角不中矩雨邊相等者日梯形如第五固速及角俱不等者日無法形如第六圖。

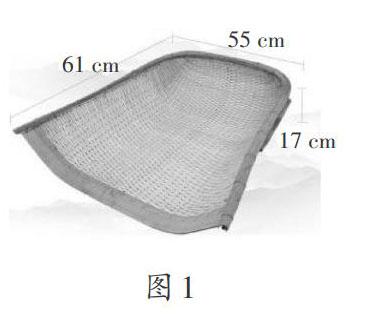
其中的“斜方形”就是現今的直角梯形;“梯形”就是現今的等腰梯形。當然，“梯形”作為數學名詞，到底第一次是不是出自此書，杜知耕是不是第一個用的人，筆者沒有查到。但不管怎樣，可以說，第一次在數學上用“梯形”（雖然當時只表示等腰梯形）這個名詞的人，是善于觀察生活，并能對生活進行抽象和提煉的人，也是發現用“梯形”比用“箕田”更能說明等腰梯形特征的人。因為簸箕底面的形狀只是近似等腰梯形（如圖1），可以說，用“梯形”更能說明數學中的梯形為什么這么定義，以及為什么上底短、下底長的人，是清楚梯形的中位線定理及其在生活中怎么應用的人。實在令人欽佩！為什么這么說呢？請看下面的分析。

二、數學中梯形有關概念來源于生活

其實，“梯形”作為數學概念來源于梯子的形狀，也就是形狀像梯子（格）的圖形。為解釋清楚，有必要對梯子的構造做具體分析。

1.梯子的結構

自古以來，梯子就是勞動人民用于上下攀爬的一種常用工具，農村和城鎮家庭中幾乎都有。只是古代的梯子大都是木質的，現今農村中木質梯子也較多，而城市中金屬梯子較多。關于梯子的結構參見木質梯子豎著的圖片（如圖2）。制作梯子時，一般是用兩根比較長且略粗一些的木頭（有些直接采用比較合適的兩棵樹的樹干）并排做梆，然后截取若干根適合攀爬的短木頭（一樣粗細）做橫桿——橫撐，再將橫撐榫卯在兩梆之間，制成如圖2所示形狀。為了安全與方便，梯子的下面寬一些，橫撐長一些，兩梆也粗一些;往上逐漸縮窄，橫撐逐層變短，兩梆也逐漸變細。這樣制成的梯子重心靠下，將梯子豎起來（下面較寬的一頭著地）斜靠在墻上時，不僅省力，因為重心較低，梯子也放得穩當，增加了攀爬的安全性。由于任何兩根橫撐都是平行的，且相鄰兩橫撐間的距離相等，既方便人們上下攀爬，也提高了安全性。

當然，有些梯子梆的兩頭一樣粗細且兩梆平行，有的是為了制作省事，有的是為了實現伸縮功能（伸縮梯子），等等。

2.梯形圖形的抽象提煉與有關概念的合理性

據上分析，結合圖2可知：梯子的任何兩根橫撐及其之間的兩梆圍成的部分（下稱“梯子格”），它們的形狀都具有兩撐平行且之間的兩梆不平行的共同特征。若把兩根橫撐及其之間的兩梆抽象成線段，這樣的四條線段圍成的圖形就是數學上的梯形（嚴格說是等腰梯形），如梯形ABCD、梯形EFGH等。之所以叫梯形是因為圖形的形狀是梯子格的形狀，也可寬泛地說是形狀像梯子的圖形。這樣一來，梯形為什么定義成只有一組對邊（代表橫撐）平行，而另一組對邊（代表兩橫撐所夾兩梆）不平行的四邊形就很自然了，因它源于制造梯子時安全與方便的需要。

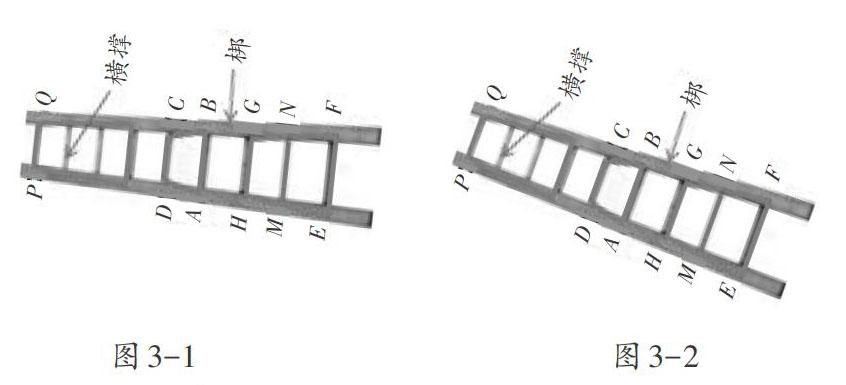
另外，梯形兩底中，短的是上底，長的是下底之界定也就符合常識了。因梯子不用時，為了安全和少占用空間，人們將梯子的一梆平放于地斜倚在墻根（另一梆倚墻）（如圖3-1），或平放在地上;也有的將較窄的一頭的一梆斜靠在比較矮的物體上，如側立斜倚在墻上（如圖3-2），這樣再用時豎起來還省功省力一些。甚至為了特殊的需要，人們也可能將梯子較窄的一頭朝下豎起來。但不管怎樣放置，對梯子來說，哪根橫撐在上，哪根橫撐在下是不變的。如圖3-1、3-2中的橫撐AB、DC，DC始終是在AB上面的一根橫撐，AB始終是在CD下面的一根橫撐，不因梯子擺放位置的不同而改變。這就是數學中規定梯形的兩底中較長的底是下底，較短的底是上底的原因。因為根據梯子的結構，上面的橫撐比下面的橫撐短。