打造“活潑潑地”小學(xué)數(shù)學(xué)課堂

徐純

[摘要]具有生氣的、活潑的課堂是每一個(gè)教師所追求的。那么該如何打造出活潑的課堂呢？不妨從培養(yǎng)學(xué)生的學(xué)習(xí)興趣入手，讓學(xué)生在教師設(shè)計(jì)的教學(xué)情境中漸入佳境，不僅能打造活潑的數(shù)學(xué)課堂，還能有效培養(yǎng)學(xué)生的科學(xué)思維和創(chuàng)造性思維。

[關(guān)鍵詞]小學(xué)數(shù)學(xué);興趣;課堂教學(xué)

[中圖分類號(hào)]

G623.5

[文獻(xiàn)標(biāo)識(shí)碼]A

[文章編號(hào)] 1007-9068（ 2020） 20-0092-02

“活潑潑地”系杜威的學(xué)生，民國(guó)教育家汪懋祖先生的教育主張。那么，我們的小學(xué)數(shù)學(xué)課堂應(yīng)怎樣“活潑潑地”進(jìn)行教學(xué)？其實(shí)只要教師不斷思考，不斷實(shí)踐，就能夠讓數(shù)學(xué)課堂變得生動(dòng)活潑，且富有個(gè)性。以下便是筆者的一些思考。

一、激發(fā)興趣，為課堂注入不竭動(dòng)力

俗話說，興趣是最好的老師。興趣在學(xué)生學(xué)習(xí)過程中發(fā)揮著巨大的作用。那么，什么是學(xué)習(xí)的興趣，學(xué)習(xí)的興趣到底與動(dòng)機(jī)、好奇心等內(nèi)在心理傾向一致嗎？顯然不是。《普通心理學(xué)》一書指出興趣是一個(gè)人為了滿足自己的某種需要而經(jīng)常從事某種活動(dòng)，并且在活動(dòng)過程中得到了愉悅的體驗(yàn)，這時(shí)候需要就可能轉(zhuǎn)化成為興趣。概括來說興趣的三個(gè)特征是“經(jīng)常性”“愉悅性”“轉(zhuǎn)化而來”。

比如，教師在課堂上精心設(shè)計(jì)了一個(gè)誘人的教學(xué)導(dǎo)語，可能激起學(xué)生學(xué)習(xí)數(shù)學(xué)的好奇心，但是不能說激發(fā)了學(xué)生的學(xué)習(xí)興趣。又如，學(xué)生最近兩天得到了老師的表揚(yáng)，開始樂于做數(shù)學(xué)題目了，這也不能說是培養(yǎng)了學(xué)生的學(xué)習(xí)興趣。只有持之以恒地愛上數(shù)學(xué)這門學(xué)科，才能說學(xué)生的興趣得到了激發(fā)。然而激發(fā)學(xué)生的興趣為小學(xué)數(shù)學(xué)教師帶來了巨大的挑戰(zhàn)。因此，在教學(xué)中，教師要引發(fā)學(xué)生思考，激發(fā)學(xué)生的興趣，讓學(xué)生愛上數(shù)學(xué)。例如，在教學(xué)“加法交換律和結(jié)合律”時(shí)，通過教師講述“朝三暮四”的故事，學(xué)生認(rèn)識(shí)到不管是3+4，還是4+3，結(jié)果（總數(shù)）不變。讓學(xué)生不僅輕松愉快地進(jìn)入新知的學(xué)習(xí)，更是把數(shù)源于數(shù)的數(shù)學(xué)思想貫穿其中，既激發(fā)了學(xué)生的學(xué)習(xí)興趣，又使課堂氛圍輕松起來。

二、引發(fā)思考，促使學(xué)生漸入佳境

學(xué)生是學(xué)習(xí)的主體，教師是學(xué)生學(xué)習(xí)的組織者、引導(dǎo)者和合作者。教師在課堂上要善于組織、引導(dǎo)學(xué)生，使學(xué)生在自主學(xué)習(xí)的過程中漸入佳境。

例如，在教學(xué)行程問題時(shí)，教師該如何引導(dǎo)學(xué)生掌握行程問題的一般解題思路呢？富有教學(xué)藝術(shù)修養(yǎng)的教師會(huì)采用潛移默化、潤(rùn)物細(xì)無聲的方法進(jìn)行教學(xué)。第一步，設(shè)置生活情景，讓學(xué)生明白S=vt。第二步，通過兩個(gè)人同時(shí)相向而行，然后相遇，在提示速度和時(shí)間的基礎(chǔ)上，讓學(xué)生理解路程的解題方法是求和。第三步，讓學(xué)生先求出一個(gè)單位時(shí)間里兩個(gè)人的速度和，然后再求出若干個(gè)單位時(shí)間里的路程總和。第四步，引導(dǎo)學(xué)生思考不是同時(shí)出發(fā)的行程問題又如何求解。

在上述教學(xué)過程中，第一步是打基礎(chǔ)的階段;第二步是建立在第一步的基礎(chǔ)之上，稍作提高;第三步是對(duì)第二步的變形，本質(zhì)沒有變化;第四步可以轉(zhuǎn)化成前面幾個(gè)步驟的形式來求得。引導(dǎo)講究的是巧妙地設(shè)計(jì)問題，從學(xué)生的學(xué)習(xí)實(shí)際出發(fā)，激發(fā)他們的好奇心。引導(dǎo)要不留痕跡，逐步提高，不可跳躍，雜亂無章，需要教師在課前進(jìn)行精心設(shè)計(jì)，讓學(xué)生在不知不覺中進(jìn)人數(shù)學(xué)學(xué)習(xí)的廣闊天地。

三、培養(yǎng)科學(xué)思維，讓學(xué)生終身受益

什么是科學(xué)思維？通俗來說，科學(xué)思維就是用科學(xué)的方法進(jìn)行思考學(xué)習(xí)。小學(xué)數(shù)學(xué)對(duì)學(xué)生的啟蒙，最根本的就是思維方式的啟蒙。教師應(yīng)盡可能讓學(xué)生利用科學(xué)思維，且課堂教學(xué)設(shè)計(jì)應(yīng)從培養(yǎng)學(xué)生的科學(xué)思維人手。

教學(xué)設(shè)計(jì)可以分為六個(gè)環(huán)節(jié)：提出問題一猜想假設(shè)一制定方案一實(shí)施探究一展示交流一拓展創(chuàng)新。在提出問題階段，教師可以引導(dǎo)學(xué)生認(rèn)真觀察、思考，并在觀察、思考中提出問題，為探究活動(dòng)做好準(zhǔn)備。在猜想假設(shè)階段，學(xué)生要圍繞發(fā)現(xiàn)的問題，進(jìn)行預(yù)測(cè)或做假設(shè)性解釋。在制定方案階段，要引導(dǎo)學(xué)生圍繞剛才的假設(shè)，提出活動(dòng)的大致思路，為接下來的科學(xué)驗(yàn)證做好準(zhǔn)備。在動(dòng)手動(dòng)腦的探究階段，要圍繞目的、方法步驟、分工、注意事項(xiàng)、時(shí)間五個(gè)方面展開，處理好“放”和“收”的關(guān)系。在展示交流階段，先小組討論，再全班進(jìn)行客觀評(píng)價(jià)，注重多次交流。在拓展創(chuàng)新的階段要注意引導(dǎo)學(xué)生運(yùn)用知識(shí)解決現(xiàn)實(shí)問題。

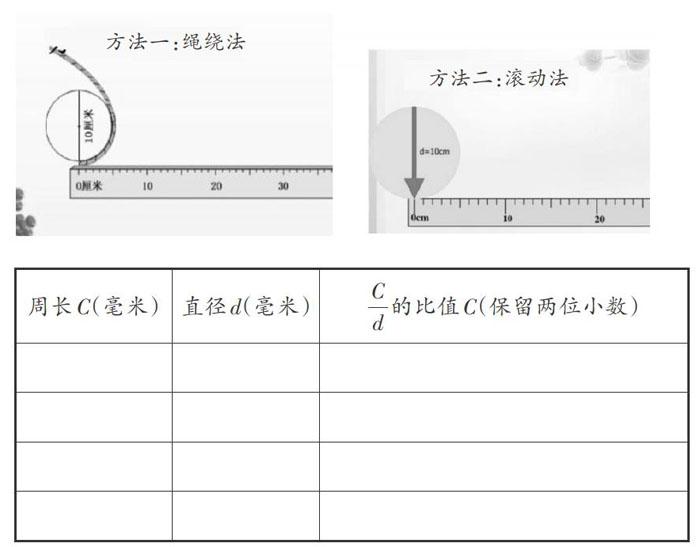
例如，在教學(xué)圓周的知識(shí)時(shí)，給學(xué)生分發(fā)一些圓形紙片，然后讓學(xué)生提出關(guān)于圓周的問題。有的學(xué)生可能就會(huì)思考“圓周和圓直徑有什么關(guān)系？”或提出某種假設(shè)“圓周和直徑應(yīng)該有一定的聯(lián)系，要不然為什么圓的直徑越大圓周就越長(zhǎng)呢？它們之間會(huì)不會(huì)存在某個(gè)比例關(guān)系呢？”接下來，指導(dǎo)學(xué)生制定活動(dòng)方案，可以圍繞繩繞法或者滾動(dòng)法制定。接著進(jìn)行實(shí)驗(yàn)和探究，把不同圓的周長(zhǎng)和半徑分別記錄在表格上，通過分析和計(jì)算得出圓周和直徑的比值。

最后發(fā)現(xiàn)這個(gè)比值大都接近一個(gè)基本恒定的數(shù)——π。科學(xué)思維就是這樣的一個(gè)過程：發(fā)現(xiàn)問題，提出假設(shè)，進(jìn)行實(shí)驗(yàn)，最后解決問題。用事實(shí)說話，培養(yǎng)學(xué)生的探究能力和科學(xué)思維的習(xí)慣，可以讓學(xué)生終身受益。

四、創(chuàng)造性思維，讓課堂更加靈動(dòng)

建立在一般思維基礎(chǔ)上的創(chuàng)造性思維具有廣闊性、靈活性、深刻性等特點(diǎn)。它既不受現(xiàn)有知識(shí)的限制，也不受傳統(tǒng)方法的束縛，從多角度、多側(cè)面、多層次去思考，去尋找答案是培養(yǎng)創(chuàng)造性思維的有效途徑。

例如，教師在教學(xué)例題“有一個(gè)正方形池塘，四周種樹，每邊種8棵，每個(gè)頂點(diǎn)各種1棵，每?jī)煽脴渲g的距離都相等，池塘的四周一共種了多少棵樹？”

這道題可以從不同的角度思考，如可以運(yùn)用“減多法”思考，根據(jù)條件可知，每邊種8棵，4邊就是8x4=32（棵），但每邊頂點(diǎn)的1棵算了兩次，一共多算了4棵，所以四周一共種了32-4=28（棵）樹。還可以從運(yùn)用“分類法”思考，先數(shù)正方形的一組對(duì)邊，包括兩個(gè)頂點(diǎn)，每邊種8棵，再數(shù)另一組對(duì)邊，不數(shù)兩個(gè)頂點(diǎn)的數(shù)量，每邊種8-2=6（棵），一共有8x2+6x2=28（棵）。到此，教師提問：“還有沒有其他的方法呢？”善于開動(dòng)腦筋的學(xué)生在教師的指導(dǎo)下又找到了另外一種解題思路—一“加點(diǎn)法”。正方形的4條邊不算頂點(diǎn)，一條邊種6棵，有四個(gè)頂點(diǎn)，列式為（8-2）x4+4=28（棵）。

學(xué)生在教師的指導(dǎo)下，從不同的層面進(jìn)行思考，就會(huì)有不同的解題思路，每一種思路就是一次創(chuàng)造的過程，在這個(gè)過程中，學(xué)生的思維獲得了啟迪，創(chuàng)造性思維得到了培養(yǎng)。在這樣一次又一次的拓展和深化中，課堂氣氛變得越來越活躍，學(xué)生的視野變得越來越廣闊，思維變得越來越靈動(dòng)。

數(shù)學(xué)是思維的體操，教師要善于開動(dòng)腦筋，從培養(yǎng)學(xué)生興趣，激發(fā)學(xué)生思考人手，著重培養(yǎng)學(xué)生的科學(xué)思維和創(chuàng)造性思維，打造“活潑潑地”數(shù)學(xué)課堂，讓學(xué)生的數(shù)學(xué)素養(yǎng)得到有效的提高。

（責(zé)編 覃小慧）