魅力課堂：“可能性”這一課該教什么？

蘇明強

[摘要]從課程標準的“四基”的角度分析“可能性”這一課，教學的目的應該是讓學生了解簡單隨機現象的不確定性，能說出簡單隨機現象中所有可能發生的結果，能定性描述簡單隨機現象發生的可能性大小，體會隨機思想和變中不變思想，積累基本活動經驗。

[關鍵詞]魅力課堂;可能性;課程標準的“四基”

[中圖分類號]

G623.5

[文獻標識碼]A

[文章編號] 1007-9068（ 2020） 20-0017-02

1978年，我國第一次在小學數學中增加了統計知識的教學內容，2001年，教育部頒布了《義務教育數學課程標準（實驗稿）》，第一次在小學數學教學內容中增加了概率方面的知識，包括可能性、可能性有大有小、等可能性和可能性大小表示等內容，分布在第一學段和第二學段之中，這時的“可能性”作為概率知識的起始課常常被安排在二年級或三年級。2011年，教育部頒布了《義務教育數學課程標準（2011年版）》，刪除了“可能性大小表示”的內容，“可能性”“可能性有大有小”“等可能性”這三部分內容統一安排在第二學段。對“可能性”這一節起始課，北師大版教材安排在四年級上冊第八單元第一課時，蘇教版教材安排在四年級上冊第六單元第一課時，人教版教材安排在五年級上冊第四單元第一課時。

對于“可能性”這一課，多數教師反映“教”和“不教”沒什么區別，因為即使不教，學生好像也會。于是，教師在教學中基本傾向于讓學生學會用“可能”“不可能”“一定”說一句話，如“太陽一定從西邊升起來”“太陽不可能從東邊升起來”等。這是不是類似語文課中的“造句”？這樣教的“可能性”是數學課嗎？

筆者所倡導的魅力數學教育觀認為：數學課要有數學味——思想的味道、思維的味道和思考的味道。概率課要有概率的味道，如何才能讓“可能性”這一課上出概率的味道呢？《義務教育數學課程標準（ 2011年版）》在內容標準中對這部分知識的教學提出了“在具體情境中，通過實例感受簡單的隨機現象，能列出簡單的隨機現象中所有可能發生的結果，能對一些簡單的隨機現象發生的可能性大小作出定性描述”的明確要求。下面，結合課程標準提出的教學要求，從課程標準的“四基”的角度分析“可能性”這節課究竟應該教什么、怎么教、為什么。

一、從基礎知識的角度分析

基礎知識在教學目標中屬于結果目標，“可能性”這一課的基礎知識究竟是什么？這是一個關鍵性的問題，有的教師把這節課的知識點定在“一定”“不可能”“可能”這三個詞，這就不奇怪很多教師都反映這節課“教”和“不教”一個樣，主要原因就在這里：“一定”“不可能”“可能”這三個詞確實不需要“教”，因為學生早在生活中就學會了。那么，“可能性”一課從知識的角度上看究竟應該教什么？課程標準提出“在具體情境中，通過實例感受簡單的隨機現象”的目標要求。筆者認為：“可能性”這節課應該教的知識點不是“一定”“不可能”“可能”這三個詞，而是“隨機現象”。隨機現象包含兩層含義，一是在個別試驗中呈現出不確定性：二是在大量重復試驗中其結果又具有一定的規律性。因此，“隨機現象的不確定性”是本節課的具體知識點，應該達到第一水平層次的要求“了解”，作為教學目標可以表述為“了解簡單隨機現象的不確定性”。

明確了“可能性”一課的基礎知識應該教什么，下面接著探討該怎么教、為什么。從隨機現象的數學本質進行分析，一是隨機現象要求可能發生的事件至少要有2種，二是隨機現象要求隨機試驗能重復進行，因此，“拋硬幣”是一個極佳的模型。然而，如何讓學生了解隨機現象的不確定性？筆者認為：倘若僅僅把“拋硬幣”當成一個游戲活動，學生簡單地“猜一猜”“拋一拋”“說一說”是無法達到預定教學目標的。教師可以在“拋硬幣”之前先設計一個確定性的活動，再組織“拋硬幣”的活動，從“確定的”過渡到“不確定的”，讓學生形成對比。在“拋硬幣”的試驗中，不要讓學生“猜一猜”——猜硬幣落地后哪一面朝上，而應該讓學生“想一想”——想讓硬幣落地后哪一面朝上。“猜一猜”容易讓學生沉迷于游戲活動之中，“想一想”更能讓學生體會到“我們無法主觀控制硬幣落地后哪一面朝上”，這樣設計更加接近隨機現象不確定性的數學本質。

二、從基本技能的角度分析

基本技能在教學目標中屬于結果目標，“可能性”這一課的基本技能究竟是什么？這是本節課的另一個關鍵性問題，有的教師把這節課的技能點放在用“一定”“不可能”“可能”這三個詞說一件事情（或一句話）上，這就是多數教師反映這節課“教”和“不教”一個樣的另一個根本原因。那么，從基本技能的角度分析“可能性”一課，究竟該教什么？課程標準提出“能列出簡單的隨機現象中所有可能發生的結果，能對一些簡單的隨機現象發生的可能性大小作出定性描述”的目標要求。筆者認為“可能性”一課的基本技能，應該包括以下兩個方面的內容：一是說出簡單隨機現象中所有可能發生的結果（即有幾種可能），需要達到結果目標的第三層次水平“能”（相當于“掌握”）;二是定性描述簡單隨機現象發生的可能性大小，需要達到結果目標的第三層次水平“能”（相當于“掌握”）。因此，“可能性”一課在基本技能方面，作為教學目標可以具體表述為：能說出簡單隨機現象中所有可能發生的結果，能定性描述簡單隨機現象發生的可能性大小。

明確了“可能性”一課的“基本技能”應該教什么以后，就該討論怎么教，以及為什么了。第一，在“拋硬幣”活動中，不能讓學生僅僅沉浸在游戲活動的歡樂之中，而應該讓學生在每一次游戲活動之前先“想一想”，再“說一說”有幾種可能發生的情況，以及為什么。第二，在概率知識的學習歷程中，描述隨機現象發生的可能性大小，需要經歷一個從定性描述到定量描述的過程，定性描述是用“一定”“不可能”“可能”三個詞語進行描述，定量描述是用“1”“0”“大于0小于1的分數”進行描述。“可能性”一課，要讓學生學會用“一定”“不可能”“可能”定性描述隨機現象發生的可能性大小，而不是讓學生學會用這三個詞說一件事（或一句話）。比如，在“拋硬幣”活動中，不是讓學生用“可能”描述這個游戲活動的全過程，說“硬幣落地后可能正面朝上，也可能反面朝上”，而是應該讓學生根據“拋硬幣”的一個隨機事件（如硬幣落地后正好正面朝上），選擇適當的描述性詞語，描述這個隨機事件發生的可能性大小（可能）。因此，教學時，教師可以先敘述隨機現象中的一個隨機事件，然后讓學生定性描述這個隨機事件發生的可能性大小，這才是本節課應該達到的技能目標要求。

三、從基本思想的角度分析

基本思想是數學課程標準的“四基”的重要內容，在教學目標中屬于過程目標。數學思想是指數學知識、方法在更高層次上的抽象與概括，數學思想常常蘊涵在數學知識的形成、發展和應用過程中。一般認為，數學基本思想有抽象思想、推理思想和建模思想，抽象思想包括集合思想、分類思想、符號表示思想、對應思想、數形結合思想、變中不變思想、極限思想等;推理思想包括轉化思想、歸納思想、類比思想、演繹思想等;建模思想包括簡化思想、量化思想、優化思想、函數思想、方程思想、隨機思想、統計思想等。“可能性”一課蘊涵的數學思想主要有隨機思想和變中不變思想——應該達到過程目標的第二層次水平，教學目標可以表述為“體會隨機思想和變中不變思想”。

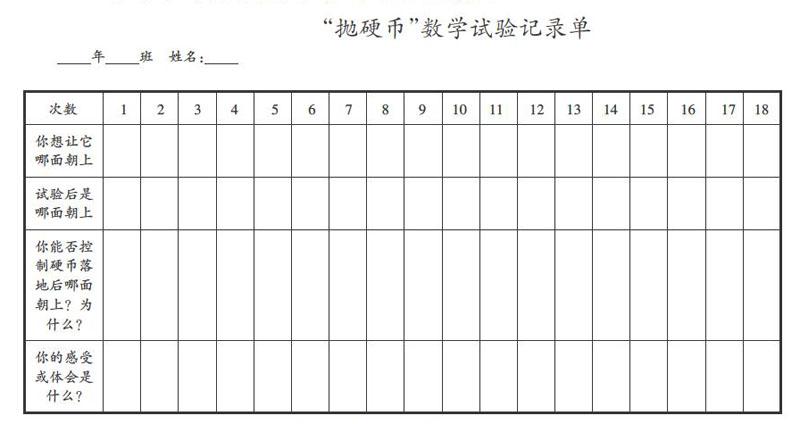
如何在“可能性”一課中融人數學思想的教學，讓學生在數學活動中體會隨機思想和變中不變思想？在“拋硬幣”這一隨機試驗中可以設計一張試驗記錄單（如下圖所示），第一欄為“你想讓它哪面朝上”，第二欄為“試驗后是哪面朝上”，要求學生每次試驗之前先填寫第一欄，試驗后再填寫第二欄，試驗18次后，看一看記錄單，想一想：能否控制硬幣落地后哪面朝上？為什么？在拋硬幣這個試驗中，什么變了？什么不變？融人數學思想的教學，關鍵在于教師的活動設計和語言啟發，以及及時引導學生進行必要的數學思考。在“拋硬幣”的數學試驗中，通過巧妙設計的記錄單，學生體會到隨機事件具有不確定性，且無法人為控制硬幣落地后是哪面朝上。在這個過程中讓學生體會隨機思想：每一次試驗是哪一面朝上是不確定的——“變”，然而所有發生的情況只有2種是確定的——“不變”，這是變中不變思想。

四、從基本活動經驗的角度分析

基本活動經驗是數學課程標準的“四基”的重要內容，在教學目標中也屬于過程目標。活動經驗是學生經歷數學活動過程的一種結果，是學生在“做”的過程和“思考”的過程中逐步積淀的，是學生在數學學習活動過程中逐步積累的，積累數學活動經驗是提高學生數學素養的重要標志。因此，幫助學生不斷積累基本活動經驗是數學教學的重要目標，主要包括觀察的經驗、操作的經驗和思維的經驗，基本活動經驗屬于過程目標的教學要求，應該達到第一層次水平，作為教學目標可以表述為：積累數學活動經驗。

“拋硬幣”在“可能性”一課中是一個簡單隨機現象的基本模型，是讓學生在試驗活動中積累數學活動經驗的重要載體。教師在組織“拋硬幣”試驗活動時，不能讓學生將其當成游戲來玩耍，而應該正確引導學生進行必要的觀察、操作和思考，不斷幫助學生積累經驗，為后續概率知識的學習奠定重要的經驗基礎。

綜上所述，“可能性”是小學概率知識的起始課，它是一節“種子課”，讓學生了解簡單隨機現象的不確定性，能說出簡單隨機現象中所有可能發生的結果，能定性描述簡單隨機現象發生的可能性大小，體會隨機思想和變中不變思想，積累基本活動經驗，從此開啟隨機現象的學習和研究之旅。這才是一節有概率味道的數學課。

（責編金鈴）