在探究學習反思中提升數學核心素養

江蘇省運河高等師范學校 (221300) 田彥軍

反思是數學探究學習活動中必不可少的一個環節.反思可以是對已經學習過的知識進行歸納梳理，將現在學習的知識與已經學過的知識進行對比，達到對知識的鞏固和再認識.當然也要對探究學習的過程進行反思，反思在探究活動的過程中的得與失，反思探究的結果是否正確、探究的方法是否合理、探究的過程是否科學.所以，在數學課堂教學中要注重學生反思能力的培養，不僅有利于學生進行查漏補缺，不斷完善自己的知識結構，而且有利于總結自己在探究活動中的經驗、方法，促進自身全面的發展.學生不僅要對自己反思，還要對他人進行反思，取長補短.實際上，在開展探究學習的過程中，不可能一下抓住數學的本質，必須要經過不斷的探究和反思，才能洞察數學活動的本質特征，提高自身的數學素養.

1.對探究活動所涉及的知識進行反思

在探究學習活動中，要求學生對運用到的知識進行反思，所運用的知識是不是很清楚，是不是真正理解了，是不是能在原有的認知基礎上有了更高的認識，是不是原來對知識的理解有偏差，是什么原因導致認識的偏差，在以后的學習中該注意什么.通過對知識的反思,學生不僅鞏固了以前學過的知識，而且對原有知識的理解更加深刻，記憶更加清楚，豐富自己的知識結構.如果學生沒有對探究學習中所涉及的知識進行反思，那么對知識的認識是膚淺的，運用知識去解決問題時就有可能出錯.

案例1 如果lgx=lga+3lgb-5lgc，那么( ).

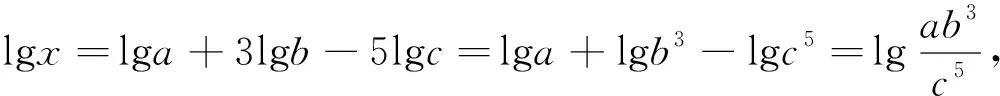
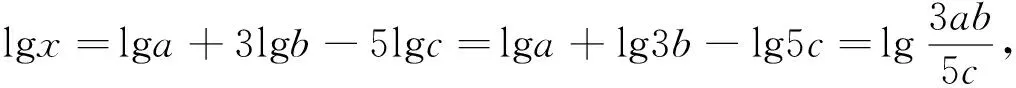
學生誤解的原因是根本沒有真正掌握對數的運算法則，不知道對數的運算法則是怎么來的.所以，對于對數運算法則理解不到位，和以前學習的運算法則混淆了，在運用法則去運算時出錯是必然的.要避免這種現象的發生，就必須讓學生真正探究對數的運算性質，并反思這種運算性質與以前學習的運算性質有哪些區別，抓住對數運算的精髓，才能掌握對數運算的實質含義.

2.對探究活動中的思維過程進行反思

在一個數學探究活動結束后，應該慢一些、停下來，讓學生回味在探究的過程中的所想所做.如在進行操作時是怎么想的,為什么這樣想，想了哪些問題,這些問題有研究的價值嗎，在操作驗證的過程中又遇到了哪些新的問題，這些問題怎么解決，這種方法為什么沒有想到，是什么原因阻礙了思維的發展等等.這樣的反思可以培養學生的學習能力,可以逐漸提高他們的數學素養,也是新課程標準對培養適應社會發展人才的要求.

案例2:求證：等軸雙曲線上任一點到對稱中心的距離是它到兩焦點距離的等比中項.

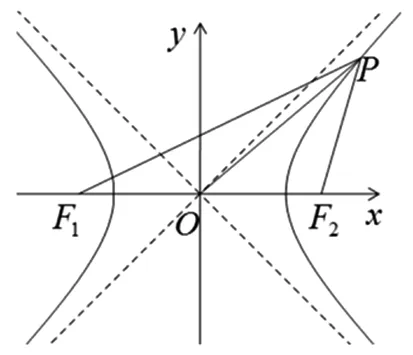
圖1

只需要證明|PO|2=|PF1|·|PF2|即可.

學生經過幾分鐘的計算.

師：好算嗎？

生：計算有點復雜.

師：你有什么好辦法嗎？(學生小組討論)

生：利用雙曲線的定義將|PF2|=

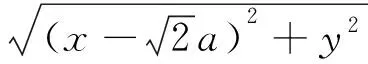
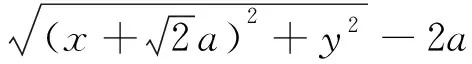
師：很好！請給這位同學掌聲，這樣可以簡化化簡的過程.

學生又經過幾分鐘的計算.

師：好算嗎？

生：還是不太好算.

師：將|PF1|·|PF2|與|PO|2的結果進行對比， 你有什么發現？

生：|PO|2的結果沒有根號，把根號去掉試試，將根號下的式子配成完全平方.

學生繼續計算.

師：怎么樣？配出來了嗎？

生：利用等軸雙曲線的方程得y2=x2-a2，將根號中的y2換掉，就可以配成完全平方了.

數學教學的過程就是對學生進行思維訓練的過程，數學教學活動就是學生的思維活動，數學教學的成功就是學生思維品質的形成和思維能力的提高．在數學課堂上要盡可能讓數學思維得到真實、自然的展現. 只有讓學生親自經歷探究帶來的困惑，才能促使學生反思推導雙曲線的標準方程時如何化繁為簡的，把推導雙曲線的標準方程的思維遷移到這道題目上來，從而達到解決問題的目的.如果在學習《雙曲線及其標準方程》這一課時，課后沒有進行反思，在解決上面的問題時就會出現偏差，解題必然受阻.所以，對思維過程進行反思，是使探究學習成為有意義學習的一個非常重要的環節.

3.對探究活動中所蘊含的數學思想方法進行反思

在數學學習的過程中，蘊含了很多的數學思想方法，學生想要很好的掌握這些思想方法就要在探究學習的過程中體會、領悟、應用.如果教師直接告訴學生這里體現了什么思想方法的話，那么學生的理解不可能深刻，當遇到需要利用這種數學思想方法解決問題時，學生還會很茫然.所以，學生要在探究學習的過程中，通過不斷地“反思—實踐—反思”，歸納出這種數學思想方法的特點，才能更好地掌握、運用這種數學思想方法，從而提高學生分析問題、解決問題的能力.

案例3:橢圓的幾何性質

(1)自主先學、小組討論

我們從哪幾個方面來研究橢圓的幾何性質？怎樣來研究？

生1：從范圍、對稱性、頂點、離心率四個方面來研究.

(2)交流展示

生2：我是從圖形來研究橢圓的性質的.根據圖形我們可以發現橢圓位于直線x=±a和y=±b的矩形里.

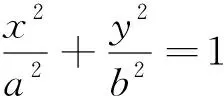
生4：將橢圓分別沿著x,y軸對折重合，說明橢圓關于x,y軸對稱；將橢圓的一半拿起來繞著原點旋轉180°重合，說明橢圓關于原點成中心對稱.

生6：觀察橢圓，可以發現有四個頂點，分別令x=0，y=0求得坐標為(±a,0),(0,±b).

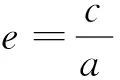
(3)質疑拓展

師：剛才幾位同學說的很好.有的同學利用代數的方法來研究橢圓的性質，如生1和生3，有的同學利用幾何的方法來研究幾何性質，如生2和生4，還有的既利用代數的方法，又利用幾何的方法，如生5和生6，這就是我們熟悉的數形結合的思想，這給以后我們研究其他的曲線的幾何性質提供了方法.對這幾條性質你還有要補充的嗎？

生8：橢圓的離心率怎樣反映了橢圓的扁平程度？

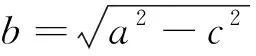
師：下面我利用幾何畫板來給大家演示一下.(利用多媒體輔助教學)如果a=b，則c=0，兩個焦點重合，這時就是圓了.

正如華羅庚先生所言，“數缺形時少直覺，形缺數時難入微，數形結合無限好，割裂分家萬事休.”數形結合，主要指的是數與形之間的一一對應關系，把抽象的數學語言、數量關系與幾何直觀、位置關系相互結合，使復雜問題簡單化，抽象的問題具體化.研究橢圓的幾何性質的過程中充分利用了數形結合的思想，使得探究出來的性質既形象又具體，由從“形”的感性認識上升到“數”的理性認識，為后續探究其他曲線性質或者解決問題提供了方法指導.

總之，在數學探究學習的過程中，學生要不斷反思自己所學、所想、所做，才能深入數學內部，抓住數學的本質，掌握知識的真諦，提高思維水平，實現核心素養的真正提升.