圖指方向，依形輔數(shù)
——一道解析幾何題的解法探究

新疆烏魯木齊市實驗學(xué)校 (830026) 符強如

在每年的全國各地的高三模擬試卷中，總有一些亮眼的試題.2020年烏市一模壓軸題本身表述簡潔，蘊含豐富的數(shù)學(xué)思想，是一道既能提供豐富教學(xué)內(nèi)容的優(yōu)質(zhì)題，又能利于拓展想象力并激發(fā)學(xué)生思維的靈活性，其鮮明的導(dǎo)向性和研究價值，符合新課改對數(shù)學(xué)核心素養(yǎng)的考查要求.筆者通過深入探析并多角度展現(xiàn)解題思路，希望對同仁教學(xué)有所借鑒.

(1)求曲線E的方程;

現(xiàn)主要探討第(2)問.

圖1

圖2

角度三：面積問題可通過仿射變換思路探路.橢圓仿射變換后成為半徑為1的圓，如圖3，M′又是A′B′的中點，所以A′B′⊥C′D′,且C′D′為直徑，A′C′B′D′面積即為弦長

圖3

通過仿射變換實現(xiàn)化橢為圓，將復(fù)雜問題轉(zhuǎn)化為熟悉的圓的問題，利用圓的性質(zhì)大大簡化了計算.其對橢圓中最值、角度、定值、證明等問題，起到優(yōu)化計算的效果.在近幾年的高考中也是屢次出現(xiàn).

高考鏈接：

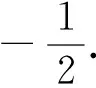
證明：△PQG是直角三角形；(ⅱ)求△PQG面積的最大值.

提示：通過仿射變換，△P′Q′G′為直角三角形，再結(jié)合夾角定理，將S△P′Q′G′用一個變量∠P′Q′G′表示出來易求最值.

提示：通過仿射變換后，將所求問題與平面幾何知識-三角形的相似結(jié)合，再利用△OA′B′是等腰三角形，易得證.

3.(2015年全國Ⅱ卷理)已知橢圓C:9x2+y2=m2(m>0)，直線l不過原點O且不平行于坐標(biāo)軸，l與C有兩個交點A，B，線段AB的中點為M．

(1)證明：直線OM的斜率與l的斜率的乘積為定值；

提示：通過仿射變換后，平行四邊形OA′P′B′成為菱形，再利用其性質(zhì)易得斜率.

結(jié)語：圖在解析幾何的解題過程中是無聲的語言，圖也是……