目標引領 問題驅動 活動啟智

陳燕軍

【摘要】課堂除了知識與技能的掌握，更要注重在教學中促進學生的主體意識、創新精神和素養的發展，而有目標引領、有正向問題、有數學活動的課堂可以驅動學生激活舊知、獨立思考、解決問題和提升素養。

【關鍵詞】設計與思考;弧長和扇形的面積;素養

筆者參加了全市教學展示活動，且教學設計“弧長和扇形的面積”獲得與會專家好評。本設計圍繞“目標引領、問題驅動、活動啟智”的思路展開，現將其設計和思考呈現如下。

一、設計簡述

1.生活引學，激活舊知

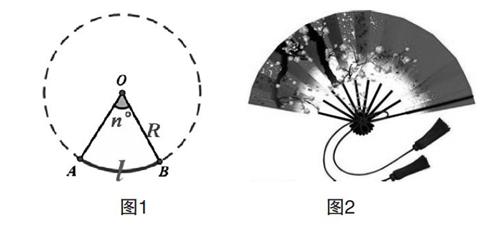
問題1：在小學，我們學過了圓和扇形，曉得扇形是圓的一部分（如圖1）。請同學們回想，圓的周長公式、面積公式分別是什么？

設計意圖：激活舊知，做好知識鋪墊。

問題2：我們知道，如圖2扇子是一個扇形，試指出該扇形的半徑、圓心角、弧。那扇形的面積、弧長又分別是指什么呢？

設計意圖：強化關鍵，明確弧是一段曲線，是圓周的一部分，弧長是這段曲線的展直長度。

問題3：將閉合的扇子徐徐打開，圓心角逐漸變大，在這個過程中，扇形弧長和扇形的面積如何隨著圓心角的變化而變化？它們之間到底有什么樣的關系呢？

設計意圖：自然引入課題，并為后面的函數視角打下伏筆

2.問題驅動，活動啟智

數學活動一：探索弧長計算公式

如圖1，已知扇形的半徑為R，圓心角度數為n，試求該扇形的弧長

問題1：當n為多少度時，扇形的弧長最容易求？舉例并說明理由。

設計意圖：研究問題，常常是從最簡單或者最特殊的情形入手的。引導學生從圓心角為180。（半圓周）、90。（四分之一圓周）、450等簡單情形入手。

問題2：上述例子我們是根據什么來求弧長的？能給我們以什么啟示？

設計意圖：引導學生感悟局部與整體之間的關系 ?弧長占整個圓周長的幾分之幾，圓心角是圓周角（360。）的幾分之幾。

問題3：如果圓心角度數為n，又如何來求此扇形的弧長？試寫出推導過程。

設計意圖：通過特殊到一般、局部與整體之間的關系，學生由1。的弧長推導得到n。的弧長，經歷自主推導探索，得

問題4：觀察公式，當半徑R為定值時，弧長R與圓心角n是什么函數關系？當圓心角度數n為定值時，弧長，與半徑R又是什么函數關系呢？弧長、半徑、圓心角三個量需要知道其中任意幾個量，能求出其他的量嗎？

設計意圖：弧長公式的再認識和強化 ?呼應前面的“徐徐打開”，滲透函數觀點和方程觀點

數學活動二：探索扇形面積計算公式

已知扇形半徑為R，圓心角度數為n，試求該扇形面積s。

問題1：經歷了弧長公式的探究，你能否設計一個探究扇形面積公式的方案？

設計意圖：同樣的思路，同樣的過程，該方案由學生自主設計，討論交流，展示結論，得到公式。滲透類比思想，進一步擴大思維含量。

問題2：從前面扇子徐徐打開的過程可以知道，扇形的面積同樣隨著弧長的變大而變大。是否可以用扇形的弧長和半徑表示該扇形的面積呢？試寫出推導過程。

設計意圖：學生通過自主推導，得到公式將

4反思悟學，課后作業

略

二、設計思考

結合教學實際，筆者從以下三個方面談自己的思考。

1.設計的思路

總體遵循“目標引領、問題驅動、活動啟智”的思路，基于發展學生數學素養設計教學，著力提升素養開展教學，學生在學習數學知識的同時提升數學素養。

環節設計上，采用“目標引領”。按照教學目標，將具體的教學內容分解為具體的教學任務，如問題的提出、問題的探究、公式的認識、公式的應用等，與這些任務對應，設計了相應的教學環節，力求突出重點，直達本質，盡量減少認知負荷，把更多的時間放在更有價值的地方。

環節落實上，采用“問題驅動”。從“問什么、怎樣問、向誰問”三個方面入手，重點環節設計系列問題，每個問題都有明確的目標指向，每個問題都有一定的思維空間，讓學生在獨立思考和解決問題的過程中形成相關知識。設計時，尤其關注了“得出結論的難易”與“思維空間的大小”之間的平衡點。

知識探索上，采用“活動啟智”。數學教學應該是數學活動的教學。活動一，教師精心設計正向問題，開展引導式的數學探究活動;活動二，教師完全放手，讓學生自主設計探索方案，開展創新式的數學設計活動。

2.目標的達成

本設計達成教學目標的橋梁是數學思考與問題解決。

按照教學目標，以問題串來驅動目標的達成。如“當n為多少度時，扇形的弧長最容易求？”問題起點低，直指目標，有數學思維，學生通過特殊到一般、局部與整體的關系自主推導得到弧長公式。接著學生能類比探索弧長的方案設計出探索扇形的面積方案，得到扇形的面積公式。

整個探究過程學生領悟到了數形結合、類比、轉化、特殊到一般的數學思想，滲透了函數觀點，讓學生感悟到“知二求三”的方程觀點。學生人人參與，不同的學生在課堂上獲得不同的數學發展。

3.素養的提升

本節課不僅教給學生運用公式來解決幾個數學問題，更關注探究的過程與方法、思維與素養。教學緊緊圍繞素養設計問題，問題起點低，入口寬，且具有一定思考空間，達到直指目標的效果。整節課發展了學生幾何直觀、邏輯推理等素養，學生感悟了數學結合、類比、轉化等重要數學思想，而問題的解決，學生的發言，則提升了學生獨立思考、自主探索、合作交流和語言表達等終生必需的品格和關鍵能力。學生在課堂中積累的發現問題、思考問題、提出問題、設計方案、解決問題等經驗，為今后探究和解決數學問題提供了寶貴的經驗和萬法。

【參考文獻】

[1]金敏.聯系蘊結構，探究促發展[I]中學數學教學參考（中旬），2019（4）：5-8

[2]劉春江文化視角下素養立意的初中數學概念教學[J]中學數學教學參考（中旬），2019（4）：9—12

[3]陳華忠問題驅動，落實數學核心素養[J]小學教學設計，2019（14）