EXCEL在數學文化課程中的應用

佟玲 王春雨

摘 要

本文針對我國高校數學文化課程的現狀，闡述了引入EXCEL軟件教學的必要性。并結合教學實踐，給出了EXCEL在斐波那契數列中的應用、利用EXCEL解決牛頓問題、繪制三維圖像等應用案例。

關鍵詞

EXCEL;數學文化;案例

中圖分類號： G642;O1-4 ? ? ? ? ? ? ? ? ? 文獻標識碼： A

DOI：10.19694/j.cnki.issn2095-2457.2020.16.059

1 在數學文化課程中引入EXCEL教學的意義

數學文化課程是目前許多高校開設的一門通識類課程，學習該課程對一些數學基礎較好的學生所起到的作用不言而喻了。在高校還有一些數學基礎較差的所謂的“文科生”。通過數學文化課程的開設，可以為這類學生展示數學中的美，讓他們帶著欣賞的目光去學習課程。數學的美，美在數學方法的簡潔。對于大多數學生，不僅要學會方法，而且還要學會應用一些數學軟件，以達到事半功倍的效果。目前常用的數學軟件大多數作起來比較復雜，特別對于文科生來講不是很實用。事實上，電子表格軟件EXCEL可以處理很多專業性不是很強的數學問題。基于EXCEL具有操作的簡便性、易于學習的特點，可以在數學文化課程中引入EXCEL教學。

2 EXCEL在數學文化課程中的應用案例

2.1 EXCEL在斐波那契數列中的應用

某種病毒，攜帶者經過一個星期的潛伏期開始具備傳染能力，假設每個病毒攜帶者每星期會傳染一名未感染者，那么如果對該病毒不加以控制，由第一名攜帶者開始，8個星期以后會有多少該病毒攜帶者？12個星期以后呢？

可以將結果以列表形式給出。

這個數列就是在自然界和生活中都很常見的斐波納契數列，它的一般項為：1、1、2、3、5、8、13、21、……第一項和第二項都是1，從第三項起，每一項是它的前兩項之和。用EXCEL很容易生成斐波那契數：在單元格A2和A3中輸入1 ，在A4中輸入“=A1+A2”，選定A4單元格，向下拖拽右下角直到單元格A13，就生成了病毒攜帶者的斐波那契數列。繼續拖動，可以生成更多的斐波那契數。

斐波納契數列，也被稱黃金分割數列，我們還可以繼續利用EXCEL來研究斐波那契數列與黃金分割比之間的關系。在單元格B3輸入z=A2/A3”，向下拖拽右下角直到單元格B16，我們發現前后兩個斐波那契數的比值隨著項數的增大，逐漸趨于黃金分割比。進一步，在單元格C3輸入“=B3-0.618033989”，向下拖拽右下角直到單元格C16，我們發現這個比值與黃金分割比的差，在數“0”附近震蕩趨近于“0”。

2.2 利用EXCEL解決牛頓問題

在數學文化課中，提到趣味數學，一定要談“牛頓問題”。下面看一個模型：

受疫情影響，某工廠積壓了大量的產品生產訂單，并且每天又有等量的新的訂單，現在工廠開始復工，如果A2名工人，B2天可以生產完全部訂單產品;A3名工人，B3天可以生產完全部訂單產品。

問題：如果有A4名工人，那么多少天能生產完全部訂單產品？

我們先來分析一下這個問題，不妨把一名工人一天所生產的產品看作1，那么：

（1）A2名工人B2天所生產的產品為A2* B2，其中包括積壓訂單和每天新產生的訂單。

（2）A3名工人B3天所生產的產品為A3* B3，其中包括積壓訂單和每天新產生的訂單。

（3）1天新增長的訂單量為C2：z=（A3*B3-A2*B2）/（B3- B2）”。

（4）工廠原有的訂單量為D2：“=（A2-C2）*B2”。

（5）每天新增長的訂單需要C2名工人完成，剩下（A4-C2）名工人要生產B4“=D2/（A4-C2）”天。

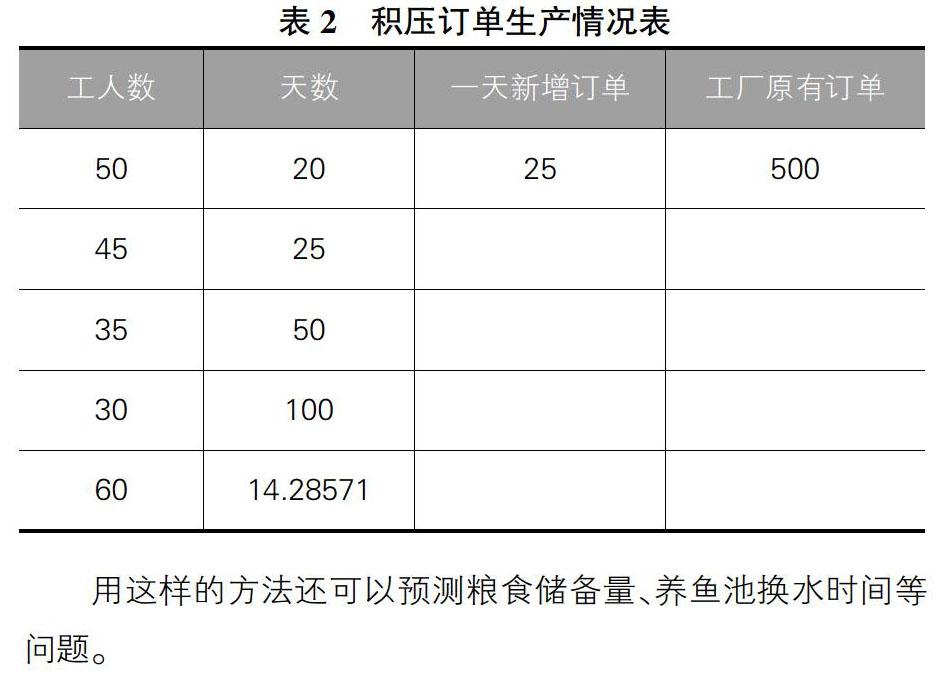
可以用具體數據來模擬一下：如果50名工人，20天可以生產完全部訂單產品;45名工人，25天可以生產完全部訂單產品。即A2=50，B2=20，A3=45，B3=25，則所需工人數與生產天數如表2。

用這樣的方法還可以預測糧食儲備量、養魚池換水時間等問題。

2.3 利用EXCEL繪制圖形

可以用EXCEL繪制漂亮的“心形線”、“星形線”、“玫瑰線”等，還可以繪制實用的幾何圖形，如空間解析幾何中常見的雙曲拋物面（馬鞍面）、橢圓拋物面等，不僅能直觀地看出曲面圖形，而且有助于用截痕法討論曲面的性質。

具體做法：

（1）在A2單元格輸入數字“20”，在A3單元格輸入數字“19”，同時選中單元格A2和A3，向下拖拽右下角直到單元格A42，這樣在第一列就產生了-20到20之間的步長為1的數據，作為變量y的取值。

（2）在B1單元格輸入數字“20”，在B2單元格輸入數字“19”，同時選中單元格B1和B2，向右拖拽右下角直到單元格AP，這樣在第一行就產生了-20到20之間的步長為1的數據，作為變量x的取值。

（4）選中生成的數據單元格B2直到單元格AP42，從菜單欄選擇“插入”→“圖表”→“所有圖表”→“曲面圖”→“三維曲面圖”單擊“確定”，這樣生成了一張曲面圖。

（5）單擊圖形，在圖表樣式中，“樣式”，選擇帶網格線的樣式（一般默認為樣式2，還要看具體情況）。“顏色”選擇單色（這里看個人喜好，一般黑白打印選擇深灰色比較好）。

（6）單擊“+”，在“圖表元素”中，勾選中“坐標軸”、“網格線”（其他項也可選）

（7）去掉圖例。

（8）在鼠標右鍵菜單中選擇“設置圖表區域格式”，選擇“無邊框”、“無填充”。

3 結語

EXCEL在數學文化課程中還有廣泛的應用，如利用EXCEL和線性規劃相關知識，可以求解博弈論中納什均衡問題，EXCEL也可以應用于誤差分析、回歸分析求解、概率統計的假設檢驗等問題中，對于數學的一些簡單應用上來說EXCEL是能完美的切合需求的。

參考文獻

[1]方守文.大學數學課堂高效教學的探索與實踐[J].教育教學論壇，2019，（12）：150-151.

[2]蔡小娜，朱亞培，溫曉楠.淺談數學實驗融入大學數學課堂[J].科教導刊（上旬刊），2018（16）：92-93.

[3]王扉，龍飛，周雙雙.？MATLAB在大學數學教學中的應用[J].數學學習與研究，2015（05）：24-25.

[4]韓明.將數學實驗的思想和方法融入大學數學教學[J].大學數學，2011（04）：137-141.