玩味旋轉(zhuǎn) 品味精彩

張 貝 李志平

[摘? 要] 文章通過改編兩個正方形的旋轉(zhuǎn)的實驗探究題，研究一類正多邊形與直角三角形、扇形等圖形的旋轉(zhuǎn)形成的重疊面積的變化問題，希望能對一線教師教學(xué)旋轉(zhuǎn)相關(guān)知識有所啟示.

[關(guān)鍵詞] 正多邊形;扇形;旋轉(zhuǎn);重疊面積;變式

正多邊形是九年級學(xué)生熟悉的圖形，由正方形的旋轉(zhuǎn)拓展到正三角形、正五邊形、正n邊形的旋轉(zhuǎn)，由特殊到一般地設(shè)計一些有規(guī)律的問題，通過讓學(xué)生實踐操作、猜想、證明、驗證，讓學(xué)生親身經(jīng)歷知識自然生成的過程，進一步提升學(xué)生對正多邊形邊角關(guān)系、全等三角形、旋轉(zhuǎn)變換等知識的理解，讓其透過旋轉(zhuǎn)表象理解常見正多邊形的性質(zhì)，歸納共性，提升解題能力，提高學(xué)生數(shù)學(xué)邏輯思維、直觀想象等核心素養(yǎng). 原題選自人教版八年級下冊第63頁實驗與探究中有關(guān)正方形的小實驗，通過旋轉(zhuǎn)一類圖形后重疊部分面積的變化問題，讓學(xué)生透過表象看到本質(zhì).

原題

如圖1，正方形ABCD的對角線相交于點O，點O是又是正方形A1B1C1D1的一個頂點，而且兩個正方形的邊長相等，無論正方形A1B1C1D1繞點O怎樣轉(zhuǎn)動，兩個正方形重疊部分的面積，總等于一個正方形面積的，想一想，這是為什么？

該實驗考查正方形的四個角是直角，對角線互相垂直平分且相等等性質(zhì)，在正方形的背景上結(jié)合三角形全等的判定和性質(zhì)來發(fā)展學(xué)生的邏輯推理、直觀想象、數(shù)學(xué)抽象等核心素養(yǎng). 本題只是考查了面積相等，那么除了面積相等我們還可以探究在旋轉(zhuǎn)過程中相等的線段等結(jié)論，因此可以在結(jié)論和條件上做些適當(dāng)?shù)淖兪?

變式

變式1? 如圖2，點O是正方形ABCD對角線的交點，將直角三角形GHI的直角頂點H與點O重合，轉(zhuǎn)動三角板使兩直角邊始終與AD，CD相交于點F，E.

（1）求證：OF=OE;

（2）試探究四邊形OEDF的面積是一個定值，并求出這個定值.

注? 在原題中涉及兩個正方形，但在旋轉(zhuǎn)正方形A1B1C1D1過程中只用到了正方形的其中一個角是直角的性質(zhì)，為此，筆者把原題中的正方形A1B1C1D1改編為直角三角形，在結(jié)論上增加考查在旋轉(zhuǎn)過程中除了面積的不變性外還有始終相等的線段的不變性.

變式2? 如圖3，點O為正五邊形ABCDE的中心，以O(shè)為頂點的扇形PFI繞點O無論怎樣轉(zhuǎn)動，要使它與正五邊形ABCDE的重疊部分的面積總保持不變，問扇形PFI應(yīng)滿足什么條件？請說明你的理由.

注? 變式2把原題中的正方形變?yōu)檎暹呅魏蜕刃危杨}設(shè)和結(jié)論進行倒置，以探究旋轉(zhuǎn)過程中重疊面積不變的核心是要保證△OHD與△OGC全等，其實質(zhì)是要讓繞點O旋轉(zhuǎn)的那個角等于中心角.

變式3? （1）如圖4（a），已知∠DOE=120°，把∠DOE的頂點放在正三角形（面積為S1）的中心點O，并將∠DOE繞點O旋轉(zhuǎn)，試求出∠DOE與正三角形重疊部分的面積.

（2）如圖4（b），已知∠GOH=90°，把∠GOH的頂點放在正方形（面積為S2）的中心點O，并將∠GOH繞點O旋轉(zhuǎn)，試求出∠GOH與正方形重疊部分的面積.

（3）如圖4（c），已知∠POI=72°，把∠POI的頂點放在正五邊形（面積為S3）的中心點O，并將∠POI繞點O旋轉(zhuǎn)，試求出∠POI與正五邊形重疊部分的面積.

（4）如圖4（d），當(dāng) ∠MON=_______度，把∠MON的頂點放在正六邊形（面積為S4）的中心點O，并將∠MON繞點O旋轉(zhuǎn)，則∠MON與正六邊形的重疊部分的面積為________.

（5）根據(jù)（1）（2）（3）（4）的規(guī)律，猜想當(dāng)一個角為________，把這個角的頂點放在正n邊形（面積為Sn）的中心點O，并將這個角繞點O旋轉(zhuǎn)，可以得出： 這個角與正n邊形的重疊部分的面積為________.

注? 根據(jù)正方形是特殊的平行四邊形，也是一個正多邊形，點O是正方形的中心，OA，OB，OC，OD分別是正方形外接圓的半徑，∠AOB，∠BOC，∠COD，∠AOD分別是外接圓的中心角，OA=OB=OC=OD，∠AOB=∠BOC=∠COD=∠AOD，所有的正多邊形都具有這些性質(zhì)，因此，筆者把題設(shè)中的正方形改編為正三角形、正五邊形、正六邊形，由特殊到一般地去探究這一類正多邊形旋轉(zhuǎn)面積不變的共性.

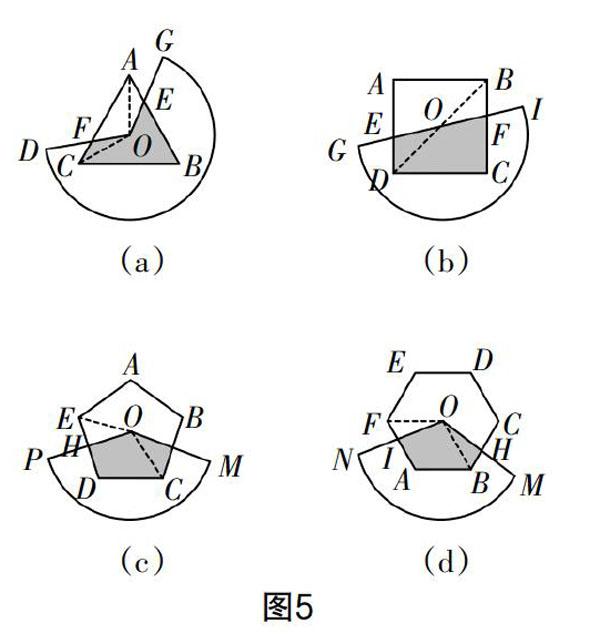
變式4? （1）如圖5（a），正三角形（半徑為a1，面積為S1）的中心點O和圓心角為240°的扇形DOG（半徑為b，且b>a1）的頂點重合，使扇形DOG繞點O旋轉(zhuǎn)，求出圖中重疊部分的面積.

（2）如圖5（b），正方形（半徑為a2，面積為S2）的中心點O和圓心角為180°的扇形GOI（半徑為b，且b>a2）的頂點重合，使扇形GOI繞點O旋轉(zhuǎn)，求出圖中重疊部分的面積.

（3）如圖5（c），正五邊形（半徑為a3，面積為S3）的中心點O和圓心角為144°的扇形POM（半徑為b，且b>a3）的頂點重合，使扇形POM繞點O旋轉(zhuǎn)，求出圖中重疊部分的面積.

（4）猜想：如圖5（d），正六邊形（半徑為a4，面積為S4）的中心點O和圓心角為________度的扇形MON（半徑為b，且b>a4）的頂點重合，使扇形MON繞點O旋轉(zhuǎn)，圖中重疊部分的面積為_________;

（5）根據(jù)（1）（2）（3）（4）的規(guī)律，猜想當(dāng)圓心角為_______度的扇形，把這個扇形的頂點放在正n邊形（半徑為b，且b>an）的中心點O，并將這個扇形繞點O旋轉(zhuǎn)，可以得出： 這個扇形與正n邊形的重疊部分的面積為_______.

注? 變式4在變式3的基礎(chǔ)上繼續(xù)拓展到扇形的圓心角是正多邊形的中心角度數(shù)的整數(shù)倍時，再將有關(guān)圖形適當(dāng)組合，就可以得到一系列在旋轉(zhuǎn)過程中，重疊部分面積不變的若干問題.

小結(jié)

通過對課本實驗題進行適當(dāng)?shù)母木帲岊}目變活了，學(xué)生的思維容量增大了，課堂也豐富了，更激發(fā)了學(xué)生探究的欲望. 教師可以通過變式訓(xùn)練讓學(xué)生在學(xué)習(xí)過程中發(fā)現(xiàn)問題的本質(zhì)，加深對同類型、同系列數(shù)學(xué)問題的理解，幫助學(xué)生總結(jié)歸納解這一類題的方法和規(guī)律.

總之，在課堂教學(xué)中我們要讓學(xué)生有深度和廣度地思考有價值的數(shù)學(xué)問題，鼓勵學(xué)生大膽猜想、驗證與證明. 教師對一道題不能就題論題，要進行適當(dāng)?shù)耐卣购脱由欤谕卣购脱由爝^程中要滲透轉(zhuǎn)化、建模、從特殊到一般等數(shù)學(xué)思想，最終達到提升學(xué)生分析問題、解決問題的能力的目的.