淺談對數學統一美的探索與運用

錢美芹

[摘? 要] 面對新課程改革的挑戰，教師需善于挖掘數學本身所特有的美，以數學美去感染和啟發學生，讓學生從靈感和頓悟中深刻感受到數學之美. 數學美包括多個方面，文章著重結合實例，從數學方法、數學結論、研究過程等方面，談談關于數學統一美的一些淺顯的見識.

[關鍵詞] 初中數學;數學方法;數學結論;研究過程;統一美

數學具有抽象性的特征，不少學生感受不到數學的美，可以體驗到的是它的枯燥無味. 事實上，世界上缺乏的不是美，而是對美的鑒賞. 數學學科不僅孕育著前人對生活中奧秘的探究，還蘊含著人類觀察社會的心智和對美的不斷追求. 數學的美無處不在，如抽象美、對稱美、符號美等，這些多姿多彩的美和諧建構為一個統一體，因此，統一是數學的本質和歸宿. 在初中數學教學的實際過程中，運用數學和藝術的眼光觀察和發現，充分挖掘其中的數學美，讓學生感受到數學的統一美，可以提升學生數學學習的興趣和學習數學的能力，點燃熱愛數學的熱情，培養數學學科的核心素養和綜合素質，以實現素質教育的有效踐行. 本文對挖掘蘊含在數學教與學過程中的統一美這一命題進行分析和探究，結合教學片段談談自身的一點拙見.

數學方法的和諧與統一

在浩瀚無邊的數學解題中，數學常用的解題方法多種多樣，如消元法、圖像法、代入法等，它們都是十分重要的解題方法，同時有著廣泛的應用性. 當然，對于具體數學問題的解決可以有特殊的解決方法，而對于一類數學問題，則更強調的是通法，通過數學方法的和諧與統一，達到以一法通一類的效果，如，我們可以通過消元法將兩元或兩元以上的方程問題轉化為一元方程問題進行解決. 讓學生掌握解決這一類問題的方法，從而找到打開這一類問題大門的“鑰匙”，形成一類問題的解題思路，真正做到心中有數地學習. 同時，教師還需關注到一題多解的訓練，以此激發學生發現解題思路中的統一性，不僅有助于探尋到多個不同的解題思路和方法，感受到數學方法的和諧與統一，還有利于學生的思維從發散向著創新推進，富有個性地解決數學問題.

案例1？搖 如圖1，請試著計算五邊形ABCDE的內角和.

學生經過思考，形成了以下多種多樣的解法：

方法1：如圖2所示，可將這個五邊形劃分為三個三角形，進而計算出內角和為540°;

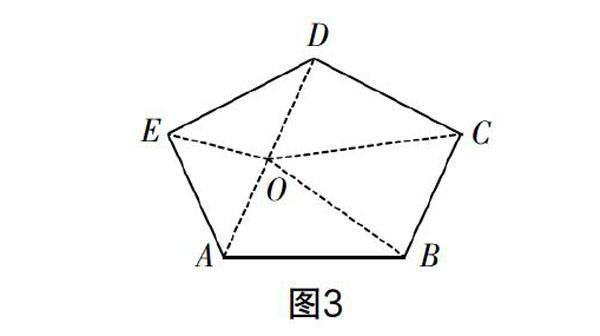
方法2：如圖3所示，在該五邊形內任意取一點O，即可將五邊形劃分為五個三角形，進一步求和即可得出內角和為540°;

方法3：如圖4所示，在該五邊形的一條邊AB上取任意的一點P，即可將其劃分為四個三角形，進一步求和即可得出內角和為540°.

通過以上3種解法，學生進一步歸納和概括得出以下統一特征：①均轉化為三角形的內角和進一步求解;②均通過頂點與其他點的連接來解決. 通過以上的概括，教師還可以提出以下高質量的問題：若這一任意一點在該五邊形外側，那是否一樣可以求出該五邊形的內角和呢？通過高階思維的引領，使其成為培養學生理性精神和創新能力的催化劑，讓學生在深度學習中感受數學方法的統一美.

評注? 在解決一道數學問題時，往往有著各種各樣的數學方法，這些方法之間又都具有一定的統一性. 上例中的一題多解就是方法統一性與多樣性的體現，讓學生通過探究得到解決問題的多個路徑，并對具體方法進行概括和總結，幫助學生真正理解問題本質，實現思維的鍛煉和深化，感受數學的統一美，這樣的思維過程遠比教師直接灌輸而獲得的能力更重要.

數學結論的和諧與統一

和諧與統一是數學美的最高境界. 若將數學比作一座金碧輝煌的宮殿，那統一美就是這座宮殿的建筑特色，不管是從其局部還是從整體入手觀察，都可以感受到它的渾然一體和相互呼應的美感. 在自然科學中，人們一直都未停止過對統一結論的追求，這對于數學學科來說更是顯而易見的. 結論的統一是數學家們從未放棄的追求，數學中的公式和定理皆是一類問題的統一結論，更是對其高度的總結和概括，如，在數的概念中，從自然數延伸到無理數，再生長到復數，數的概念的研究不斷擴充，不斷延伸，從而進行統一的概念性規劃，實現數學的統一美.

案例2？搖 從定理“平行四邊形的對角線相互平行”延展談起.

問題1：圖5中共有多少條不同的線段？

問題2：圖6中一共有多少個小于180°的不同角？

問題3：足球場上一共有n支足球隊在比賽，采用的是單循環制，那么共需比賽的場數是多少？

問題4：一大型聚會共有n人參加，見面后每兩個人都需握手一次，那么一共需握手的次數是多少？

......

評注? 觀察以上問題，不難看出這些問題的背景皆不相同，內容也毫無關聯，但均有著驚人的統一——結論的統一，也就是■. 課堂教學是師生交流和生生互動的場所，若是教師能有意識地挖掘，在教學中靈活巧妙地安排好每一個教學環節，指導好學生的歸納和理解，就能讓學生在數學理解的層面上感受到數學的魅力，真正意義上感受到美的熏陶，進而感受到數學帶來的趣味性和美的享受，讓學生在美的熏陶中學好數學.

研究過程的和諧與統一

數學的統一美不僅強調數學方法和數學結論的統一，在數學教學中還應著力剖析數學研究過程的和諧與統一，如一些幾何圖形的研究過程都需經歷“定義—性質—識別—應用”的研究階段. 解題過程中的統一美從未停止過，在理解中感受解題過程的統一性，可以進一步優化認知結構，提升關鍵性能力.

案例3? 如圖7，已知平面直角坐標系xOy中，點A（10，0）. 以OA為直徑，在第一象限內作半圓，且點B為該半圓的圓周上的一動點，連接OB，AB，并延長AB至點D，使得DB=AB. 再過點D作x軸的垂線，與x軸和直線OB分別交于點E，F，E為垂足，連接CF.

（1）當∠AOB=30°時，試求出弧AB的長度.

（2）當DE=8時，試求出線段EF的長.

（3）隨著點B的不斷運動，是否存在以點E，C，F為頂點的三角形相似于△AOB？若存在，求出點E的坐標;若不存在，請闡明原因.

解：（1）略

（2）①如圖8，當交點E在A，C之間時，連接OD.

因為DB=AB，OB⊥AD，所以OA=OD=10.

又DE=8，所以OE=6，所以AE=4.

又△FOE～△ADE，所以EF ∶ AE=OE ∶ DE，從而解得EF=3.

②如圖9，當交點E在點O左側時，連接OD.

因為DB=AB，OB⊥AD，所以OA=OD=10.

又DE=8，所以OE=6，所以AE=16.

又△FOE～△ADE，所以EF ∶ AE=OE ∶ DE，從而解得EF=12.

（3）略.

評注? 從上述解題過程可以看出，盡管第（2）問中的兩種情形在圖形和結論上都表現出較大的差異性，但在解題過程中卻能做到基本統一，讓學生在感受統一性的同時，實現數學思維的突破.

伽利略曾說過：數學總是美的，數學是美的科學. 數學的統一美可以消除學生枯燥乏味的成見，讓學生感受到數學是一個五彩斑斕的美的世界. 在初中數學教學中，數學的統一美不僅表現在以上三個方面，而且存在于教學的多個環節之中，需要我們廣大數學教師融合藝術與數學進行挖掘與提煉，建構學生崇尚真理的情感與精神力量，使其感受到數學的無窮魅力，由此才能更好地發揮數學教育的價值.