含間隙振動系統周期振動的多樣性和轉遷特征

呂小紅 羅冠煒

摘要： 以兩自由度含間隙碰撞振動系統為研究對象，辨識周期振動的模式類型及其在雙參平面內的發生區域和分布規律，揭示低頻區域無沖擊、基本沖擊、顫碰和亞諧沖擊等周期振動模式類型的多樣性和轉遷特征，以及擦邊分岔點附近鞍結分岔的存在與位移振幅的變化形式之間的關系。在無沖擊和基本沖擊振動的邊界線上存在若干具有自相似分形特征的舌形域。舌形域內亞諧振動的模式類型和分布具有規律性。由于擦邊分岔的不可逆性，擦邊和鞍結分岔線在相鄰周期振動的發生區域之間形成遲滯域，并在舌形域的邊界形成一個遲滯域群。相鄰遲滯域邊界線的橫截相交點是奇異點，只有在奇異點，位移振幅連續變化，擦邊分岔連續可逆。揭示了奇異點的二重擦邊和倍化-鞍結余維二分岔特征。

關鍵詞： 非線性振動; 分岔; 間隙; 碰撞; 雙參耦合

中圖分類號： O322; TH113.1 文獻標志碼： A 文章編號： 1004-4523（2020）04-0688-10

DOI：10.16385/j.cnki.issn.1004-4523.2020.04.006

引 言

在機械動力系統中，由于間隙和運動限幅機構的存在，常常導致剛性部件在運行中發生碰撞振動[1-2]。為了消除碰撞對機械設備帶來的不利影響或為了提高利用碰撞振動原理設計制造的機械裝置的工作性能，國內外學者通過理論分析、數值仿真和實驗等方法對碰撞振動系統的周期振動穩定性與分岔[3-5]、混沌激變[6-7]、吸引子共存[8]、控制與反控制[9]等相關問題進行了研究。由于碰撞、擦邊接觸等非線性因素，使得一些常規的光滑動力系統的定性分析方法難以直接應用于該類系統的動力學研究。Nordmark[10]發現碰撞振動系統存在一種特殊形式的碰撞即擦邊碰撞，通過構建Poincaré-Nordmark局部映射研究了系統在擦邊分岔點鄰域內的動力學行為。Nordmark在此領域的研究工作為后續擦邊分岔及奇異性研究奠定了理論基礎。其后，國內外學者借助沖擊映射和不連續幾何拓撲等方法研究了碰撞振動系統的余維一、余維二擦邊分岔以及在擦邊分岔點鄰域內的動力學特性[11-18]。

碰撞振動系統在低頻條件下的顫碰振動是一個不可忽視的動力學現象。Nordmark和Piiroinen[19]構建了碰撞振動系統顫碰-黏滯振動的局部不連續映射，研究了顫碰振動的穩定性與局部分岔。馮進鈐等[20]應用彗尾映射分析了Duffing單邊碰撞系統的顫振運動和兩種顫振分岔。Wagg[21-22]數值模擬了兩自由度碰撞振動系統的顫碰和黏滯振動現象，并討論了周期黏滯振動的多重滑移分岔。Hs和Champneys[23]研究了機械壓力溢流閥的擦邊分岔及閥和閥座間的顫碰振動特性。據統計，由于異常振動造成機械設備的重大事故多表現為非線性低頻振動失穩，但該失穩機理至今還未被研究清楚，因此，碰撞振動系統的低頻振動特性及分岔特點仍是學術界研究的主要內容之一，而且已有的對碰撞振動系統的周期振動與分岔等問題的研究報道基本都是取一個系統參數為分岔參數進行研究的，不能較全面地揭示動力學與系統參數的關聯。本文基于雙參平面研究兩自由度含間隙碰撞振動系統周期振動的模式類型、發生區域和分布規律，著重分析系統在低頻區域表現的無沖擊、基本沖擊、顫碰和亞諧沖擊等周期振動的分岔，揭示系統周期振動模式類型的多樣性和轉遷特征，擦邊分岔點附近鞍結分岔存在與否的機理，以及無沖擊和基本沖擊振動的發生區域邊界線上的二重擦邊和倍化-鞍結余維二分岔。

1 力學模型

兩自由度含間隙碰撞振動系統的力學模型如圖1所示。質量塊Mi（i=1， 2）通過剛度為Ki的線性彈簧和阻尼系數為Ci的線性阻尼器連接于支承，兩個質量塊之間通過剛度為K3的線性彈簧和阻尼系數為C3的線性阻尼器相連。質量塊Mi上作用有簡諧激勵力Pisin（ΩΤ+τ）。用X1和X2分別表示質量塊M1與質量塊M2的位移。當X1-X2=B時，兩個質量塊發生碰撞。碰撞過程中的能量損失由碰撞恢復系數R確定。系統中的阻尼為Rayleigh型比例阻尼。

2 周期振動的模式類型和Poincaré映射

在不同的系統參數條件下，圖1所示系統可能呈現不同模式類型的周期振動或混沌。用p/n區分周期振動的類型，n和p分別表示一個振動周期內的激勵力周期數和兩個質量塊之間的碰撞次數。0/n（p = 0）表示無沖擊振動，系統在振動過程中（x1-x2）max<δ，兩質量塊不發生碰撞。無沖擊振動一般存在于高頻區域或低頻大間隙區域，此時系統為兩自由度線性振動系統，其運動狀態僅由方程（2）的解決定。1/n （n ≥ 2）單沖擊亞諧振動表示兩個質量塊相鄰兩次碰撞之間的時間間隔為Tn = 2nπ/ω。

當激勵頻率ω和間隙δ比較小時，系統可能呈現p/1（p = 1， 2， 3， …）類基本沖擊振動。系統的振動周期為一個激勵力周期（T1 = 2π/ω， n = 1）不變，但兩個質量塊在一個振動周期內的碰撞次數p會隨著系統參數的變化而變化。ω或δ越小，p越大，一個激勵力周期內的碰撞次數越多。當ω或δ足夠小時，p為一個很大的有限值，這類碰撞稱為非完整顫碰振動。非完整顫碰振動隨著ω或δ的繼續減小，顫碰振動的末次沖擊速度最終趨向于零，引起兩個質量塊黏滯振動。有黏滯振動過程的顫碰振動稱為完整顫碰振動。非完整和完整顫碰振動分別用/1和/1表示。

3 相鄰周期振動的轉遷規律

圖1所示系統共有8個量綱一參數：μm， μk1， μk2，ζ，f，δ，ω和R，其中激勵頻率ω和間隙δ對系統動力學的影響最大，因此，本文取ω和δ為分岔參數，應用映射σn和σp辨識周期振動的模式類型及其在雙參平面內發生區域，然后結合單參數分岔圖、相圖和擾動映射理論等方法確定邊界線的分岔類型，揭示含間隙振動系統周期振動模式類型的多樣性及相鄰周期振動的演化規律。基于量綱一參數的取值范圍，取μm=0.5， μk1=0.5， μk2=0.5，ζ=0.1， f=0和R=0.8，數值計算ω在0.1-8.0，δ在0-0.8變化時的雙參數（ω， δ）分岔圖如圖2（a）所示。

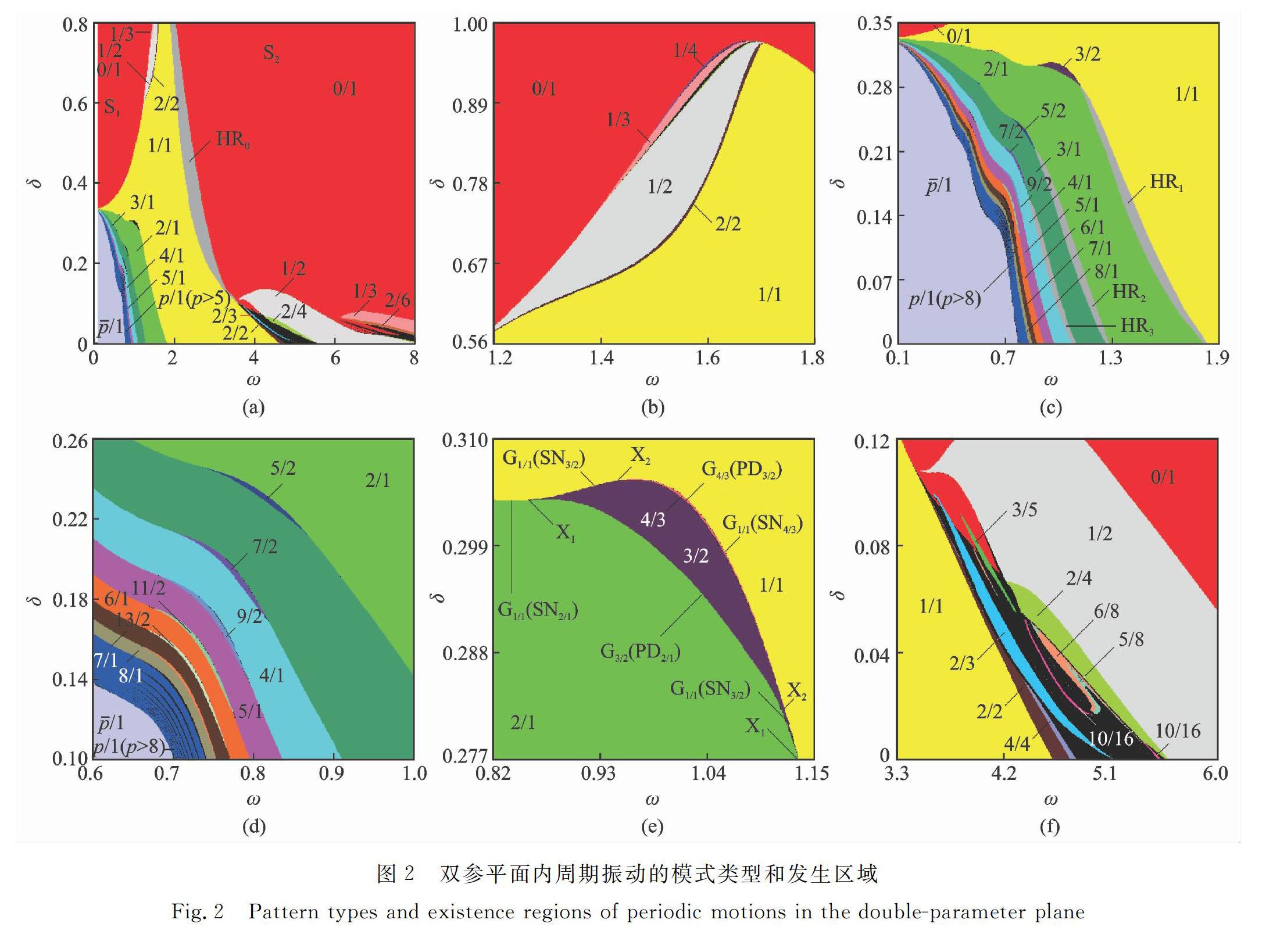
圖2（a）清晰地呈現了（ω， δ）平面內周期振動的模式類型、發生區域和分布規律。在大間隙區域，除了1/1基本沖擊振動的發生區域及其邊界上的遲滯域和舌形域以外，系統在其余參數區域內呈現0/1無沖擊振動。圖2（b）為舌形域內亞諧振動的模式類型及其參數島分布的放大和細節描述。隨著δ的減小，系統周期振動的模式類型逐漸呈現多樣性。在高頻區域，出現了1/n和2/（2n）等亞諧振動的發生區域;在低頻區域，出現了p/1基本沖擊振動、/1非完整顫碰振動和/1完整顫碰振動的發生區域。p/1類基本沖擊振動的發生區域隨著p的增大，從右向左依次呈帶狀域分布，其面積逐漸減小。圖2（c）為圖2（a）中低頻小間隙區域基本沖擊振動和顫碰振動的放大。圖2（d）揭示了在相鄰基本沖擊振動之間的舌形域內，亞諧振動的模式類型具有規律性。圖2（e）描述了基本沖擊振動1/1和2/1之間的舌形域內亞諧振動的參數島及分岔線類型。圖2（f）為1/1振動與1/2振動之間演化的局部放大。

3.1 0/1振動與1/1振動的轉遷過程

如圖2（a）所示，0/1無沖擊振動的發生區域被有碰撞振動的發生區域分割為兩個子區域S1和S2，其與1/1基本沖擊振動的發生區域之間的分界線為0/1振動的擦邊分岔線G0/1或1/1振動的鞍結分岔線SN1/1，分岔線類型跟分岔參數的變化方向相關。在子區域S1增大ω，在子區域S2減小ω，或在子區域S1和S2減小δ穿越G0/1，0/1振動經擦邊分岔產生1/1振動。在1/1振動的發生區域變化ω或增大δ穿越SN1/1，系統經鞍結分岔轉遷為0/1振動。兩條分岔線G0/1和SN1/1之間形成一定的遲滯域，見圖2（a）標有HR0的灰色區域（子區域S1與1/1振動的發生區域之間的遲滯域很窄，圖中沒有標出）。0/1振動和1/1振動在遲滯域共存。以δ=0.5為例，ω雙向穿越圖2（a）所示遲滯域HR0時的單參數分岔圖如圖3（a）所示。圖中，縱坐標為每個激勵力周期內的最小相對位移（x1-x2）min，橫坐標標目的頂標“”表示分岔參數增大和減小雙向變化。減小ω，0/1振動的最小相對位移逐漸增大。當ω=2.1306（G1點）時，（x1-x2）min=δ，兩個質量塊擦邊碰撞，系統表現為0/1擦邊振動。繼續減小ω，0/1振動經擦邊分岔產生1/1振動。最小相對位移（x1-x2）min在擦邊分岔后發生了跳躍。當ω增大時，1/1振動在SN1點（ω=2.3753）經鞍結分岔轉遷為0/1振動。穩定的0/1振動和1/1振動在G1和SN1之間的遲滯區共存。

如圖2（a）所示，在子區域S1與1/1振動的發生區域之間存在一個舌形域。圖2（b）為此舌形域的細節描述。舌形域內，系統主要表現為1/n （n ≥ 2）類單沖擊亞諧振動，其發生區域可稱為相應亞諧振動的參數島。舌形域內，1/n振動的參數島由下而上依次分布，n依次增大，面積依次減小。子區域S1與舌形域之間存在一個很窄的遲滯域群。每個遲滯域的右邊界線為0/1振動的擦邊分岔線，左邊界線為1/n振動的鞍結分岔線，兩條分岔線橫截相交于兩個奇異點。0/1振動和1/n振動的相互轉遷只有在奇異點是連續可逆的，兩者經擦邊分岔相互轉遷，鞍結分岔消失。圖3（b）和圖3（c）為0/1振動與圖2（b）所示舌形域內的1/n （n=2， 3）振動經遲滯域群相互轉遷的雙向分岔圖。由圖3（b）可見，增大ω，0/1振動在G2點（ω=1.22665）經擦邊分岔產生1/2振動。兩個質量塊的最小相對位移在G2點后發生了跳躍。減小ω，1/2振動在SN2點（ω=1.22521）經鞍結分岔轉遷為0/1振動。穩定的0/1振動和1/2振動在G2和SN2之間的遲滯區共存。0/1振動和1/3振動在G3點（ω=1.43108）或SN3點（ω=1.431002）經擦邊或鞍結分岔相互轉遷，如圖3（c）所示。

為了詳細分析圖2（b）所示舌形域內1/n單沖擊亞諧振動的分岔特點，取ω = 1.6，δ垂直穿越該舌形域時的單參數分岔圖如圖3（d）和（e）所示。圖3（d）為每個激勵力周期內的最小相對位移（x1-x2）min隨δ減小（藍色）和增大（紅色）的分岔圖。圖3（e）為質量塊M1的碰前速度1-隨δ增大的分岔圖，圖中橫坐標標目的頂標“→”表示分岔參數增大。圖3（f）為圖3（e）中1/2振動發生周期倍化分岔的放大圖。結合圖3（d）和（e）兩個分岔圖，可以辨識周期振動在一個振動周期內的激勵力周期數n和碰撞次數p，從而確定p/n振動。圖3（d）和（e）中，1/n（n=2， 3， 4）單沖擊亞諧振動的窗口清晰可見。減小δ分別穿越δ=0.94405和δ=0.92512時，1/4和1/3振動經擦邊分岔轉遷為混沌。當δ=0.76346時，1/2振動經擦邊分岔產生1/1振動。增大δ穿越δ=0.79308時，1/1振動經倍化分岔產生2/2振動，然后當δ=0.79312時，2/2振動經鞍結分岔產生1/2振動。由于1/2振動的擦邊分岔的不可逆性，在2/2振動的鞍結分岔點和1/2振動的擦邊分岔點之間的遲滯區δ∈（0.76346， 0.79312）內，1/1和1/2振動，或2/2和1/2振動共存，如圖3（d）所示。圖4（a）給出了δ=0.78時，系統共存的1/1振動（紅色）和1/2振動（藍色）的相圖。圖4（a1）為圖4（a）的局部放大。1/2振動的相軌線表現為一次碰撞軌線和一次非碰撞軌線。減小δ，1/2振動的非碰撞軌線逐漸靠近碰撞面。當δ減小至δ=0.76346時，非碰撞軌線與碰撞面擦邊接觸，如圖4（b）和圖4（b1）所示。穿越擦邊分岔點，1/2振動經擦邊分岔產生1/1振動，并與已經存在的1/1振動的相軌線重合。由上面的分析可知，圖2（b）所示舌形域與1/1振動的發生區域之間存在一個遲滯域，其右邊界為1/2振動的擦邊分岔線，左邊界為2/2振動的鞍結分岔線。兩條分岔線橫截相交于兩個奇異點，連接著舌形域左邊界上的遲滯域群，因此，奇異點既是0/1振動的二重擦邊分岔點，也是1/1振動的倍化-鞍結余唯二分岔點。

Humphries和Piiroinen [25]以單自由度周期激勵碰撞振子為例，應用不連續幾何的拓撲方法解釋了擦邊分岔點附近鞍結分岔存在與否的原因，但是這種方法很難直接應用于多自由度碰撞振動系統。由前面的分析可知，如果碰撞振動系統的位移振幅在擦邊分岔后出現跳躍，則在擦邊分岔點附近存在鞍結分岔，并形成遲滯區。相鄰兩類運動經擦邊分岔或鞍結分岔相互轉遷，分岔類型與分岔參數的變化方向相關。如果位移振幅在擦邊分岔后連續變化，則鞍結分岔點與擦邊分岔點重合，鞍結分岔消失。相鄰兩類運動經擦邊分岔相互轉遷，分岔過程連續可逆。關于這個結論的理論證明還有待進一步研究。

3.2 基本沖擊振動的轉遷特征

在圖2（a）所示低頻小間隙區域，系統主要呈現p/1類基本沖擊振動，/1非完整顫碰振動和/1完整顫碰振動。圖2（c）區分了p/1（p=1， 2， 3， …， 8）振動和/1振動的發生區域，p/1（p>8）振動和/1振動的發生區域歸結在一起。在相鄰p/1振動的發生區域之間，存在舌形域和遲滯域兩類過渡區域。

p/1基本沖擊振動的發生區域的邊界線呈現波浪狀，在每個波段的峰值位置出現一個舌形域。所有舌形域具有自相似分形特征，面積自右向左依次減小。由圖2（d）可見，在p/1振動和（p+1）/1振動之間的舌形域內，可見（2p+1）/2等（np+1）/n （n ≥ 2）類亞諧沖擊振動的參數島。舌形域的上邊界為p/1振動的擦邊分岔線Gp/1或（np+1）/n振動群的鞍結分岔線SN（np+1）/n。Gp/1和SN（np+1）/n形成一個遲滯域群。每個遲滯域內，p/1振動和相應的（np+1）/n振動共存。舌形域的下邊界為周期倍化分岔線PD（p+1）/1或擦邊分岔線G（2p+1）/2。穿越PD（p+1）/1，（p+1）/1振動產生（2p+2）/2振動而嵌入舌形域，然后經過鞍結分岔線SN（2p+2）/2轉遷為（2p+1）/2振動。分岔參數反方向變化時，（2p+1）/2振動經擦邊分岔直接轉遷為（p+1）/1振動而退出舌形域。在SN（2p+2）/2和G（2p+1）/2之間的遲滯域內，（p+1）/1和（2p+1）/2，或（2p+2）/2和（2p+1）/2共存。每個舌形域的上下邊界橫截相交于兩個奇異點，與相鄰p/1振動轉遷過程中的遲滯域相連，因此，奇異點既是p/1振動的二重擦邊分岔點，也是（p+1）/1振動的倍化-鞍結余維二分岔點。

（np+1）/n （n=2， 3， …）亞諧沖擊振動的參數島在舌形域內自下而上依次分布。當δ增大時，（np+1）/n振動或經鞍結分岔退出舌形域轉遷為p/1振動，或經周期倍化分岔產生（2np+2）/2n振動，然后經鞍結分岔轉遷為[（n+1）p+1]/（n+1）振動;減小δ，（np+1）/n振動經擦邊分岔產生[（n-1）p+1]/（n-1）振動。（np+1）/n振動的擦邊分岔使得系統的振動周期減小1個激勵力周期，一個振動周期內的碰撞次數減少p次，因此，（2p+1）/2振動的擦邊分岔因為產生（p+1）/1振動而退出舌形域。（2np+2）/（2n）振動的鞍結分岔線和[（n+1）p+1]/（n+1）振動的擦邊分岔線在相鄰（np+1）/n振動的參數島之間形成一個遲滯域。遲滯域內，（np+1）/n和[（n+1）p+1]/（n+1），或（2np+2）/2n和[（n+1）p+1]/（n+1）共存。遲滯域的上下邊界橫截相交于兩個奇異點。該奇異點是（np+1）/n與[（n+1）p+1]/（n+1），及（np+1）/n與p/1振動之間的兩個遲滯域的連接點，也是p/1振動的二重擦邊分岔點和（np+1）/n振動的倍化-鞍結余維二分岔點。

圖2（e）為存在于基本沖擊振動1/1和2/1之間的一個舌形域的細化和邊界線描述。圖中可清楚地觀察到3/2，4/3等（n+1）/n （p=1）類亞諧沖擊振動的參數島，X1和X2為奇異點。舌形域的上邊界為1/1振動的擦邊分岔線G1/1或（n+1）/n振動群的鞍結分岔線SN（n+1）/n，下邊界為擦邊分岔G3/2或周期倍化分岔線PD2/1。分岔線G1/1和相鄰的SN（n+1）/n形成一個很窄的遲滯域HR1/1∩（n+1）/n，導致在舌形域的上邊界出現至少由3個遲滯域組成的一個遲滯域群。每個遲滯域內，1/1振動和相應的（n+1）/n振動共存。舌形域與2/1振動的發生區域之間，由擦邊分岔線G3/2和鞍結分岔線SN4/2形成一個遲滯域HR2/1∩3/2。3個遲滯域HR1/1∩3/2，HR2/1∩3/2和HR1的6條邊界線橫截相交于X1點，因此，X1點既是1/1振動的二重擦邊分岔點，也是2/1振動的倍化-鞍結余維二分岔點。圖6（a）和（b）為ω=1.02，δ垂直穿越圖2（e）所示舌形域的單參數分岔圖。當δ=0.3時系統呈現3/2振動，如圖7（a）所示。減小δ至δ=0.29502時，3/2振動經擦邊分岔產生2/1振動。當δ增大至δ=0.29652時，2/1振動經周期倍化分岔產生4/2振動，然后當δ=0.29665時，2/2振動經鞍結分岔產生3/2振動。在3/2振動的擦邊分岔點和4/2振動的鞍結分岔點之間的遲滯區δ∈（0.29502， 0.29665）內，3/2和2/1振動，或3/2和4/2振動共存。圖7（b）為共存的3/2擦邊（藍色）和2/1（紅色）振動的相圖。

3.3 單沖擊振動的分岔

在圖2（a）所示高頻小間隙區域，系統主要呈現1/n（n≥2）單沖擊亞諧振動和2/（2n）亞諧振動。1/n振動的上下邊界分別為0/1振動的擦邊分岔線（或1/n振動的鞍結分岔線）和1/n振動的周期倍化分岔線。1/n振動的周期倍化分岔產生2/（2n）振動。圖2（f）為1/1振動和1/2振動之間演化的細化圖。1/n（n≥1）振動在向混沌演化的過程中，由于發生多沖擊亞諧振動的擦邊分岔，使得1/n振動的周期倍化序列中斷，只有在很小的間隙區域內，1/1振動經周期倍化序列通向混沌。在1/1振動和1/2振動之間，出現了如2/3，3/5，5/8，6/8等多沖擊亞諧振動的發生區域。

4 結 論

本文以兩自由度含間隙碰撞振動系統為研究對象，通過構建兩種Poincaré映射辨識了周期振動的模式類型及其在雙參平面內的發生區域和分布規律，詳細分析了相鄰p/1（p≥0）振動經遲滯域和舌形域相互轉遷的機理和規律，以及舌形域內亞諧振動的規律性和分岔特征。

p/1（p≥0）振動的擦邊分岔或產生（p+1）/1基本沖擊振動或（np+1）/n （n≥2）類亞諧振動。在0/1與1/1振動之間的舌形域內，1/n（n≥3）振動經擦邊分岔產生混沌，而在相鄰p/1振動之間的舌形域內，（np+1）/n振動經擦邊分岔產生[（n-1）p+1]/（n-1）振動。

在雙參平面內，相鄰p/1（p≥0）振動遲滯域和舌形域相互轉遷。舌形域內亞諧振動的模式類型和分布具有規律性。由于擦邊分岔的不可逆性，擦邊和鞍結分岔線在相鄰周期振動的發生區域之間形成遲滯域，并在舌形域的邊界形成一個遲滯域群。每個遲滯域的上下邊界橫截相交于兩個奇異點。只有在奇異點，相鄰周期振動經擦邊分岔轉遷，鞍結分岔消失。奇異點也是相鄰3個遲滯域，即6條邊界線的橫截點，因此，奇異點是p/1振動的二重擦邊分岔點和（np+1）/n（n≥1）振動的倍化-鞍結余維二分岔點。

如果碰撞振動系統的位移振幅在擦邊分岔后出現跳躍，則在擦邊分岔點附近存在鞍結分岔，并形成遲滯區;如果位移振幅在擦邊分岔后連續變化，則鞍結分岔點與擦邊分岔點重合，相鄰兩類運動在擦邊分岔點的相互轉遷連續可逆。關于這個結論的理論證明還有待進一步研究。

參考文獻：

[1] Li Xiang，Yao Zhiyuan， Wu Ranchao. Modeling and sticking motion analysis of a vibro-impact system in linear ultrasonic motors[J]. International Journal of Mechanical Sciences， 2015， 100（9）： 23-31.

[2] Chávez J P， Pavlovskaia E， Wiercigroch M. Bifurcation analysis of a piecewise-linear impact oscillator with drift[J]. Nonlinear Dynamics， 2014， 77（1-2）： 213-227.

[3] Yue Y. The dynamics of a symmetric impact oscillator between two rigid stops[J]. Nonlinear Analysis： Real World Applications， 2011， 12： 741-50.

[4] Luo G W， Xie J H. Hopf bifurcations of a two degree-of- freedom vibro-impact system[J]. Journal of Sound and Vibration， 1998， 213（3）： 391-48.

[5] Zhang Yongxiang， Luo Guanwei. Torus-doubling bifurcations and strange nonchaotic attractors in a vibro-impact system[J]. Journal of Sound and Vibration， 2013，332： 5462-5475.

[6] 馮進鈐， 徐 偉. 碰撞振動系統中周期軌道擦邊誘導的混沌激變[J]. 力學學報， 2013， 45（1）： 30-36.

Feng Jinqian， Xu Wei. Grazing-induced chaotic crisis for periodic orbits in vibro-impact systems[J]. Chinese Journal of Theoretical and Applied Mechanics， 2013， 45（1）： 30-36.

[7] Feng Jinqian. Analysis of chaotic saddles in a nonlinear vibro-impact system[J]. Communications in Nonlinear Science and Numerical Simulation， 2017， 48（7）： 39-50.

[8] Li Qunhong， Lu Qishao. Coexisting periodic orbits in vibro-impacting dynamical systems[J]. Applied Mathematics and Mechanics， 2003， 24（3）： 261-273.

[9] 伍 新， 文桂林， 徐慧東， 等. 三自由度含間隙碰撞振動系統Neimark-sacher分岔的反控制[J]. 物理學報，2015， 64（20）： 200504.

Wu Xin， Wen Guilin， Xu Huidong， et al. Anti-controlling Neimark-sacker bifurcation of a three-degree-of-freedom vibration system with clearance [J]. Acta Physics Sinica， 2015， 64（20）： 200504.

[10] Nordmark A B. Non-periodic motion caused by grazing incidence in an impact oscillator[J]. Journal of Sound and Vibration， 1991， 145（2）： 279-297.

[11] Pavlovskaia E， Wiercigroch M. Bifurcation analysis of an impact oscillator with a one-sided elastic constraint near grazing [J]. Physica D： Nonlinear Phenomena， 2010， 239（6）： 312-321.

[12] 張思進， 周利彪， 陸啟韶. 線性碰振系統周期解擦邊分岔的一類映射分析方法[J]. 力學學報，2007， 37（1）： 132-136.

Zhang Sijin， Zhou Libiao， Lu Qishao. A map method for grazing bifurcation in linear vibro-impact system[J]. Chinese Journal of Theoretical and Applied Mechanics， 2007， 37（1）： 132-136.

[13] Chillingworth D R J. Dynamics of an impact oscillator near a degenerate graze[J]. Nonlinearity， 2010， 23： 2723-2748.

[14] Ma Yue， Ing James， Banerjee Soumitro， et al. The nature of the normal form map for soft impacting systems[J]. International Journal of Non-Linear Mechanics， 2008， 43（6）： 504-513.

[15] Xu Jieqiong， Li Qunhong， Wang Nan. Existence and stability of the grazing periodic trajectory in a two-degree-of-freedom vibro-impact system[J]. Applied Mathematics and Computation， 2011， 217（12）： 5537-5546.

[16] Kryzhevich S， Wiercigroch M. Topology of vibro-impact systems in the neighborhood of grazing[J]. Physica D： Nonlinear Phenomena， 2012， 241（22）： 1919-1931.

[17] Wen Guilin， Yin Shan， Xu Huidong， et al. Analysis of grazing bifurcation from periodic motion to quasi-periodic motion in impact-damper systems [J]. Chaos， Solitons and Fractals， 2016， （83）： 112-118.

[18] Jiang Haibo， Chong A S E， Ueda Y， et al. Grazing-induced bifurcations in impact oscillators with elastic and rigid constraints[J]. International Journal of Mechanical Sciences， 2017， 127（7）： 204-214.

[19] Nordmark A B， Piiroinen Petri T. Simulation and stability analysis of impacting systems with complete chattering[J]. Nonlinear Dynamics， 2009， 58： 85-106.

[20] 馮進鈐， 徐 偉， 牛玉俊. Duffing單邊碰撞系統的顫振分岔[J]. 物理學報， 2010， 59（1）： 157-163.

Feng Jinqian， Xu Wei， Niu Yujun. Chattering bifurcations in a Duffing unilateral vibro-impact system[J]. Acta Physica Sinica， 2010， 59（1）： 157-163.

[21] Wagg D J. Rising phenomena and the multi-sliding bifurcation in a two-degree of freedom impact oscillator[J]. Chaos， Solitons and Fractals， 2004， 22（3）： 541-548.

[22] Wagg D J. Periodic sticking motion in a two-degree-of-freedom impact oscillator[J]. International Journal of Non-Linear Mechanics， 2005， 40（8）： 1076-1087.

[23] Hs Csaba， Champneys A R. Grazing bifurcations and chatter in a pressure relief valve model[J]. Physica D： Nonlinear Phenomena， 2012， 241（22）： 2068-2076.

[24] Luo G W. Dynamics of an impact-forming machine[J]. International Journal of Mechanical Sciences， 2006， 48： 1295-1313.

[25] Humphries N， Piiroinen P T. A discontinuity-geometry view of the relationship between saddle-node and grazing bifurcations[J]. Physica D： Nonlinear Phenomena， 2012， 241（22）： 1911-1918.

Abstract： A two-degree-of-freedom vibro-impact system with a clearance is considered. Diversity， existence and stability domains， and distribution regularities of periodic motions are obtained numerically in the double-parameter plane by constructing two Poincaré maps. Bifurcations of periodic motions in the low frequency region， such as impactless motion， fundamental impact， chattering and subharmonic impact motions， are analyzed. Diversity and transition characteristics of pattern types of periodic motions of the system， and relation between the existence of saddle-node bifurcation in the vicinity of the grazing bifurcation and the variation of displacement amplitude are revealed. Some small tongue-shaped regions that have self-similarity and fractal characteristic appear on the boundary of impactless motions and fundamental impact motions. Pattern type and distribution of subharmonic impact motions in the tongue-shaped regions show regularity. Given the irreversibility of grazing bifurcation of impactless motions， fundamental impact motions， and subharmonic impact motions in tongue-shaped regions， the hysteresis domain forms between the existence regions of adjacent periodic motions， and a group of hysteresis domains appear on the boundary of the tongue-shaped regions. Two boundary curves of each hysteresis zone intersect at two singular points. The grazing bifurcation is continuous and reversible and saddle-node bifurcation is absent only at these singular points. The displacement amplitude of the impact oscillator varies continuously just after them. Each singular point is the junction of adjacent hysteresis domains， and also a point of double grazing bifurcation flip-fold codimension-2 bifurcation.

Key words： nonlinear vibration; bifurcation; clearance; impact; double-parameter coupling