淺談求逆矩陣的幾種方法

◎張家寶 （南京師范大學中北學院，江蘇 丹陽 212300）

矩陣是線性代數(shù)的主要研究對象之一，在自然科學、工程技術(shù)以及管理科學中都有著廣泛的應用．求矩陣的逆矩陣在矩陣理論中有著極其重要的地位．本文將給出幾種求逆矩陣的常用方法．

一、求逆矩陣的方法

本文重點介紹求逆矩陣的具體步驟，因此對適用于高階矩陣求逆矩陣的方法，也均以三階方陣為例進行說明．

（一）利用伴隨矩陣求逆矩陣

例1設求Α 的逆矩陣．

解故Α 可逆．

各元素的代數(shù)余子式為：A11＝-2，A12＝0，A13＝1，A21＝0，A22＝-3，A23＝2，A31＝1，A32＝4，A33＝-3．

利用伴隨矩陣求逆矩陣也稱為公式法，需要先根據(jù)｜Α｜判斷矩陣是否可逆，在可逆的情況下再求A 中各元素的代數(shù)余子式，從而構(gòu)造伴隨矩陣，最后利用公式求所給矩陣的逆矩陣．該方法適用于求低階矩陣的逆矩陣，較為簡便快捷．

（二）利用初等變換求逆矩陣

若矩陣Α 是n 階可逆矩陣，可通過一系列的初等行變換將其化為單位矩陣Ε，即Ρm…Ρ2Ρ1Α ＝Ε，則Α-1＝Ρm…Ρ2Ρ1＝P．也就是說，Α 可逆，Α 的逆矩陣為一系列初等矩陣的乘積［1］．具體步驟：將n 階矩陣Α 與n 階單位矩陣Ε構(gòu)造成一個n×2n 矩陣（Α?Ε），對其進行初等行變換，化為行最簡形矩陣，此時Α 化為Ε，對應的Ε 就化為Α-1．

也可通過一系列的初等列變換將其化為單位矩陣Ε，即ΑΤ1Τ2…Τl＝Ε，則Α-1＝Τ1Τ2…Τl＝Τ．具體步驟：將n 階矩陣Α 與n 階單位矩陣Ε 構(gòu)造成一個2n×n 矩陣對其進行初等列變換，化為列最簡形矩陣即可．

例2設求Α 的逆矩陣．

解

若采用初等列變換求逆矩陣，則要注意矩陣構(gòu)造上的區(qū)別．

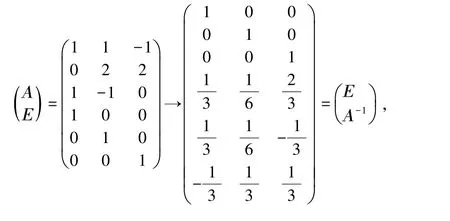
當然，初等行變換和初等列變換也可以同時使用．若n階矩陣Α 可逆，則Α 必與n 階單位矩陣Ε 等價，因此Α 可經(jīng)過有限次初等變換化為標準型，即存在可逆矩陣Ρ 和Τ，使得ΡΑΤ＝Ε，解得Α ＝Ρ-1Τ-1，Α-1＝ΤΡ．此時，需構(gòu)造一個2n×2n 矩陣，對前n 行進行初等行變換，再對前n列進行初等列變換，化為，由此解得Α-1．

故

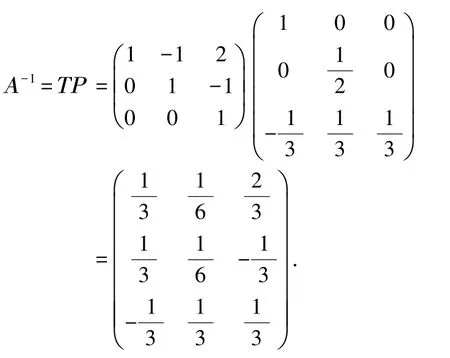
對于階數(shù)較高的矩陣，利用初等變換求矩陣的逆矩陣更為高效，并且無須判斷矩陣是否可逆．利用初等變換求逆矩陣時，我們習慣上采用初等行變換求解．

（三）利用哈密頓—凱萊定理求逆矩陣

定理［2］：設Α 是數(shù)域P 上一個n×n 矩陣，f（λ）＝｜λΕΑ｜是Α 的特征多項式，則f（Α）＝Αn-（a11＋a22＋…＋ann）Αn-1＋…＋（-1）n｜Α｜Ε＝Ο．

記f（Α）＝Αn＋a1Αn-1＋…＋an-1Α＋anΕ＝Ο，整理得

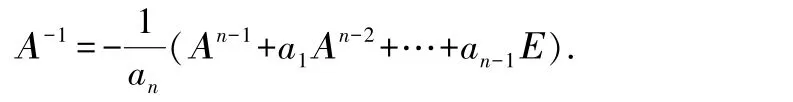
具體步驟：先求出矩陣Α 的特征多項式，再根據(jù)特征多項式相應地寫出矩陣Α 的矩陣多項式，令其等于零矩陣Ο，對所得矩陣方程進行恒等變形，求得Α-1．

求Α 的逆矩陣．

解Α 的特征多項式為

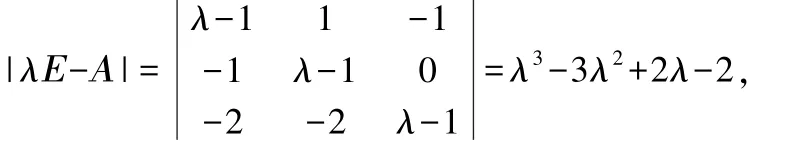
由哈密頓—凱萊定理有f（Α）＝Α3-3Α2＋2Α-2Ε＝Ο，

當矩陣階數(shù)較低時，計算量并不繁雜，利用哈密頓—凱萊定理求逆矩陣也是一種可選的方法．

（四）利用分塊矩陣求逆矩陣

例4設求Α 的逆矩陣．

二、結(jié) 論

本文給出了四種求逆矩陣的一般方法．當矩陣階數(shù)較低時，可采用公式法，利用伴隨矩陣求逆矩陣，也可利用哈密頓—凱萊定理求解；當矩陣階數(shù)較高時，可利用初等變換求逆矩陣，若分塊后具有特殊結(jié)構(gòu)，也可利用分塊矩陣求逆矩陣．