高中數學解析幾何綜合應用解題策略

■福建省仙游縣華僑中學 陳志恩

一、關于解析幾何綜合應用解題策略的簡析

處理高中解析幾何問題，策略是解題的主要方針，解題過程中需要有邏輯思維、形象思維以及直覺思維的共同作用。一般幾何問題的分析方法計算量大，但學生的計算能力較弱。即使他們找到了解決問題的方法，他們也不能做出正確的計算，得到正確的結果。對于教師而言，忽略了學生在教學過程中的主體地位。有時候，學生對教師的理解越低，教師說得越多，解釋的重復性就越高，這可以提高學生的理解水平。我認為在新課程標準的兩年內完成三年課程的教學對教師和學生都是非常苛刻的。教師往往專注于考試，他們不能用解析幾何的數學文化來激勵學生學習，不能用解析幾何的數學文化幫助學生從歷史的角度看待學習，不能用解析幾何的數學文化指導學生解決數學問題，不能用解析幾何的數學文化有效地滲透數學思想和方法。高中數學教師應該給學生多多傳授解析幾何的解題策略，讓他們感受到解析幾何的運算并非“猙獰恐怖”的，而是有章可循的，方法得當，堅持運算，也可輕松達到成功。在解析幾何的解題過程中，主要策略就是要抓住題目當中的已知條件，然后設出未知量，未知量是根據每個人對于題目條件的著眼點不同確定的，對于題目條件的先后利用順序每個人的理解可能也不同。但是在真正的解題過程中，合理地利用題目條件，將某一量作為控制變動的根源，解題中緊緊盯住結論，然后產生明確的目標意識，解題時根據解題方向不斷地調整解題思路，最終經過一系列的代數計算和公式變形，求出方程或者是函數得出題目結論。這就是解析幾何解題過程中需要注意的問題，同時選擇不同的解題方式，計算量可能差距也很大，所以對于任何一個題目都要先學會綜合考慮，然后對解題方式進行對比選擇最佳的解題思路，加強練習，這樣在今后遇到解析幾何時就能夠更好地綜合應用各個解題思路。

二、學會變式進行研究

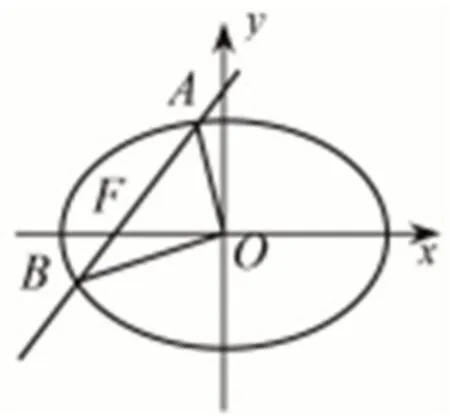
（1）求橢圓C的標準方程；

（2）已知直線與橢圓C相交于A，B兩點。

熟練掌握習題以后，我們可以更好地對習題進行改變，在這一過程中，可以更好地吃透習題，在不斷分析題目條件、要求的過程中，更好地掌握解析幾何的綜合解題思路，加強對解析幾何計算和分析題目能力的練習。對上述題目進行優化之后我們延伸出新的題目：

問題1：是否存在一個定圓和直線AB相切呢？

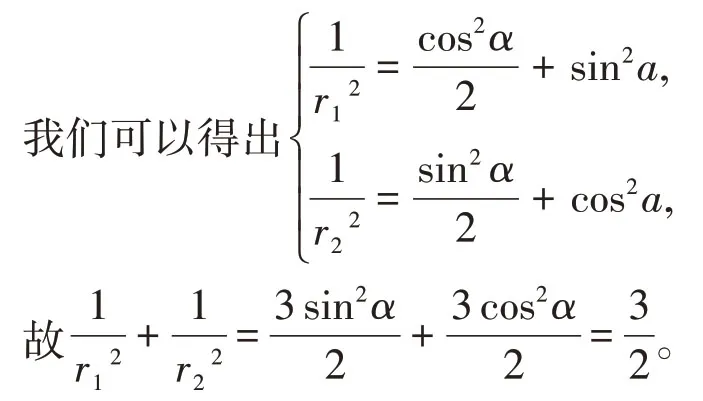
我們設點O到AB的距離是AB*d，所以

所以，在本小問我們可以加一句：證明必定存在一個圓和AB相切，其實在這里我們還能得出一個結論，如果橢圓上兩點與橢圓中心的張角成直角，那么一定有以中心為圓形的定圓與過這兩點的直線相切，在該題目當中，我們可以還通過這一方式倆求S的取值范圍，但是解析幾何的解答題每題解題過程中需要先進行論證。

問題2：那么我們是否能夠利用上述結論來解決面積的取值范圍問題？

反思上述的解題過程，通過分析如何解題領悟如何學習解題，從將信息相互整合到解決問題的過程，這個過程中與最后的驗算過程有一定的區別，解題過程需要我們不斷地去思考、推理，確保思維的嚴謹性，解題方式的最佳，同時還需要學會提煉題目的關鍵信息，所以數學解題過程中是一種創造性的活動，而解析幾何又是考查學生計算能力和綜合分析能力的題型，因此在學習解析幾何的過程中，一定要熟練提煉題目信息，多方面思考解題方式，學會對解題思路的綜合應用，實現最佳解題。

三、結語

總之，在解題的過程中方法與策略雖好，但這些也都是理論上的東西，想要真正地在解析幾何的解題過程中，對于問題能夠靈活應用各種解題方式，教師必須在教學中親力親為，必須起到引領示范作用，同時要在課堂上舍得花時間讓學生練習，只有這樣才能提高學生的解析幾何運算能力。高中數學教師在解析幾何教學過程中，一定要引導學生靈活運用各種解題策略，立足定義，巧妙利用數形結合思想，同時利用分類討論等等，提高學生在解析幾何方面的解題能力。