施行以點帶面 彰顯核心素養(yǎng)
——《方程的根和函數(shù)的零點》教學(xué)設(shè)計

牟小蘭

（重慶市萬州第三中學(xué) 重慶萬州 404000）

一、教材分析

以人教版《普通高中課程標準實驗教科書》A版數(shù)學(xué)必修一為藍本，分析第三章《函數(shù)的應(yīng)用第一節(jié)《函數(shù)與方程》的第一課時《方程的根與函數(shù)的零點》的教學(xué)內(nèi)容。本節(jié)課主要內(nèi)容是函數(shù)零點定義、函數(shù)零點與相應(yīng)方程根的關(guān)系、函數(shù)零點存在性定理，是一節(jié)概念課。本節(jié)課不僅為二分法的學(xué)習(xí)做準備，也為方程與函數(shù)提供了連接點，從而揭示兩者之間的本質(zhì)關(guān)系，這種聯(lián)系正是“函數(shù)與方程思想”的理論基礎(chǔ)，為今后進一步學(xué)習(xí)函數(shù)與不等式等其他知識聯(lián)系奠定了堅實的基礎(chǔ)，一步一步地形成學(xué)生的數(shù)學(xué)素養(yǎng)，為今后適應(yīng)社會做準備。

二、學(xué)情分析

學(xué)生已經(jīng)了解一些基本初等函數(shù)的模型，具備一定的看圖識圖能力，這位本節(jié)課利用函數(shù)的圖象，判斷方程根的存在性提供了一定的知識基礎(chǔ)。但高一學(xué)生對數(shù)形結(jié)合與抽象思維尚不能完全駕馭。因此，函數(shù)與方程相聯(lián)系的觀點的建立，函數(shù)應(yīng)用意識的初步樹立，是本節(jié)課必須承載的任務(wù)。

三、教學(xué)目標

知識與技能 理解函數(shù)零點的定義及方程的根與函數(shù)零點之間的聯(lián)系；理解函數(shù)零點存在性定理；能利用函數(shù)的圖象和性質(zhì)判斷函數(shù)的零點個數(shù)及所在區(qū)間。

過程與方法 滲透由特殊到一般的認知規(guī)律，提升學(xué)生的抽象和概括能力，領(lǐng)會數(shù)形結(jié)合、函數(shù)與方程等數(shù)學(xué)思想。

情感、態(tài)度與價值觀 認識函數(shù)零點的價值，使學(xué)生認識到學(xué)有所用；培養(yǎng)學(xué)生認真、耐心、嚴謹?shù)臄?shù)學(xué)品質(zhì)；讓學(xué)生在自我解決問題的過程中體驗成功的喜悅。

四、教學(xué)重難點

重點：理解函數(shù)零點的定義，體會方程的根與函數(shù)零點之間的聯(lián)系，掌握函數(shù)零點存在性的判斷。

難點：在合情推理中讓學(xué)生掌握體會判定定理，并能初步應(yīng)用。

五、教學(xué)方法

自主學(xué)習(xí)，合作探究，講練結(jié)合

六、教學(xué)過程

（一）課題引入（2分鐘）

某網(wǎng)店經(jīng)營的暖手袋原價x元，在某天推出五折優(yōu)惠和免郵費的促銷活動，以提高本店的銷售額度。小李同學(xué)利用支付寶里的50元在促銷期間購買此暖手袋后余額為y元。

①請幫助小李同學(xué)建立以x為自變量，y為函數(shù)的關(guān)系式（暫不考慮定義域）。

②原價為多少元時余額為0？

以非常簡單網(wǎng)購話題出發(fā)，引起學(xué)生注意，探索數(shù)學(xué)問題，激發(fā)學(xué)習(xí)興趣。

（二）自主學(xué)習(xí)（12分鐘）

引例中方程x-50=0的實根50，就是函數(shù)y=x-50的零點，所以，我們由特殊到一般，得出函數(shù)零點的定義：

對于函數(shù)y=f(x)，我們把使f(x)=0的實數(shù)叫做函數(shù)y=f(x)的零點。

理解定義，提出問題：方程的根與相應(yīng)函數(shù)的零點之間有什么聯(lián)系？

為了更好理解定義，回答該問題，我們應(yīng)像涓涓細流般慢慢地將知識浸潤于學(xué)生的心田，選用學(xué)生已知熟悉的知識來理解改知識和探究未知。

（三）組織探究（11分鐘）

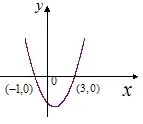
結(jié)合函數(shù)y=x2-2x-3的圖象觀察發(fā)現(xiàn)：

①在區(qū)間[-2，1]上有零點：

f(-2)=5,f(1)=-4,f(-2)·f(1)＜0

②在區(qū)間[2，4]上呢？

運用特殊到一般的學(xué)習(xí)規(guī)律，得出函數(shù)零點的存在性定理。

（四）練習(xí)反饋（5分鐘）

①函數(shù)y=x2-3x+2的零點是（ ）

A.（1，0），（2，0） B.x=1 C.x=2 D.1，2

②函數(shù)f(x)=2x-3零點所在的一個區(qū)間是（ ）

A.（-1，1） B.（0，1） C.（1，2） D.（2，3）

以上練習(xí)是基礎(chǔ)性練習(xí)，意在檢驗學(xué)生掌握基礎(chǔ)知識的情況。先請學(xué)生作答，并請一位學(xué)生作為“小老師”為大家做簡單講解后，教師再稍作點評。

（五）協(xié)作交流（8分鐘）

為了進一步運用該知識解決函數(shù)的零點問題，我們一起來看看這道例題。

例：函數(shù)f(x)=1nx+2x-6有沒有零點？有幾個零點？

分析：

①利用函數(shù)零點的存在性定理，借助計算器或計算機作出x，f(x) 的對應(yīng)值表和圖像。

②圖象法：函數(shù)y=f(x)圖象連續(xù)，f(a)·f(b)＜0，且f(x)為單調(diào)函數(shù)，則y=f(x)有且只有一個零點。

③數(shù)形結(jié)合法：函數(shù)f(x)=1nx+2x-6的零點問題，轉(zhuǎn)化為方程1nx+2x-6=0即1nx=6-2x的實根問題，有轉(zhuǎn)化為函數(shù)y=1nx和y=6-2x的交點個數(shù)問題。

（六）課堂小結(jié)（2分鐘）

①基礎(chǔ)知識：函數(shù)零點的定義；函數(shù)的零點存在性定理；確定函數(shù)零點的方法。

②思想方法：特殊到一般，數(shù)形結(jié)合，轉(zhuǎn)化與化歸，函數(shù)與方程

③責(zé)任擔(dān)當(dāng)：面對困難，勇于探索，精準探究，實現(xiàn)夢想

（七）板書設(shè)計

（八）課后鞏固

①P88 練習(xí)1

②思考題：怎樣求出函數(shù) 的零點的近似值。

③閱讀P91《中外歷史上的方程求解》，了解方程的發(fā)展歷程。

（九）課后反思

本節(jié)內(nèi)容以函數(shù)圖象為主要載體，通過本節(jié)課的學(xué)習(xí)研究，使學(xué)生從“數(shù)”“形”兩個層次理解函數(shù)零點的定義，突出“數(shù)形結(jié)合”的數(shù)學(xué)思想。在實施教學(xué)過程中指導(dǎo)學(xué)生學(xué)習(xí)方法，注重數(shù)形結(jié)合、轉(zhuǎn)化與化歸、函數(shù)與方程等數(shù)學(xué)思想的滲透，是學(xué)生對知識的掌握不僅僅停留在表面，還在更深層次的問題是思考，使數(shù)學(xué)核心素養(yǎng)的培養(yǎng)得到落實。

總之，我們要準確把握學(xué)生的認知規(guī)律，努力做到不斷完善每節(jié)課，思路流暢，層次分明，問題引領(lǐng)，關(guān)注思維，讓學(xué)生在學(xué)習(xí)中參與其中，不斷提高自身的數(shù)學(xué)素養(yǎng)。