數學問題解答

2020年6月號問題解答

(解答由問題提供人給出)

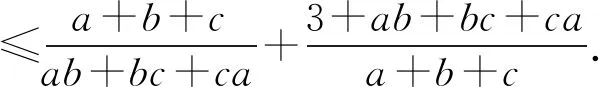
(北京粉筆未來科技有限公司 鄭小彬)

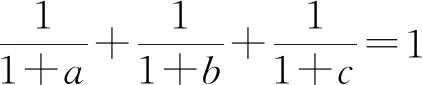
展開得abc=a+b+c+2,

則待證不等式

≤(a+b+c)2

≤2(ab+bc+ca-a-b-c),

由均值不等式有

故只需證

≤2(ab+bc+ca-a-b-c),

展開整理，等價于證

ab+bc+ca-2(a+b+c)≥0,

由均值不等式有

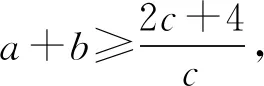
所以ab+bc+ca-2(a+b+c)

故不等式得證.

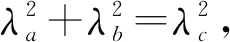
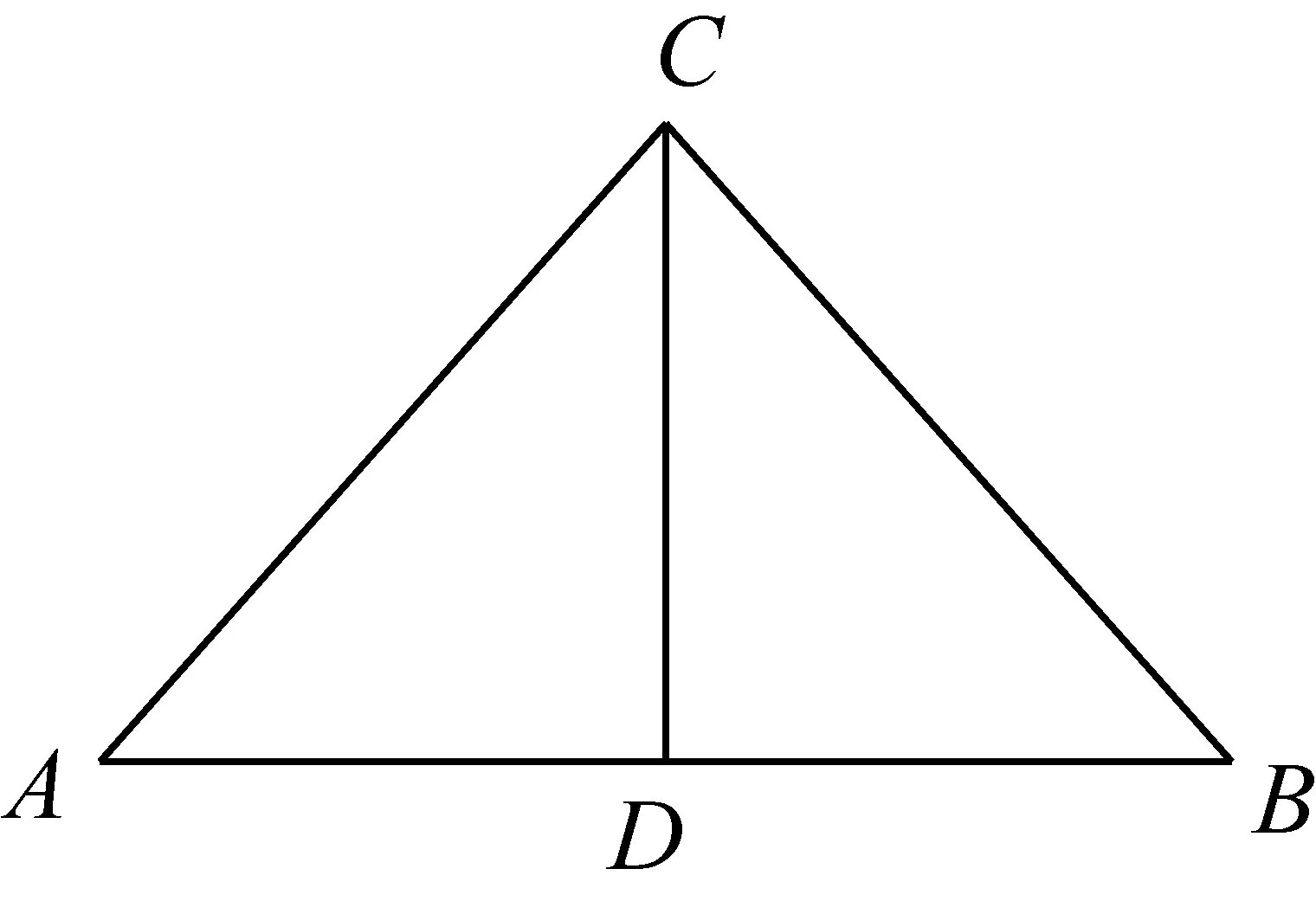
(山東省泰安市寧陽第一中學 劉才華 271400)

證明設∠BCD=α,∠ACD=β,則

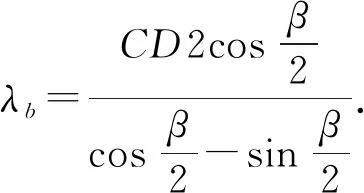
?1-(sinα+sinβ)+(cosα+cosβ)-sin (α+β)+cos (α+β)=0.

設α+β=x，則β=x-α.代入上式并整理得

(1+cosα-sinα)(1-sinx)+

cosx(1+sinα+cosα)=0

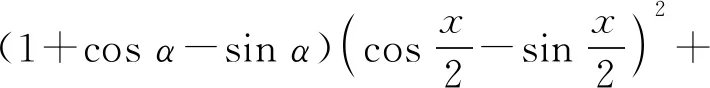
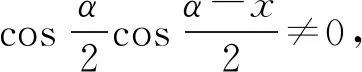
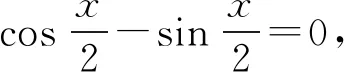
故三角形ABC是直角三角形.

2548已知m>1,求證:存在相異正數a,b,使am-alna=bm-blnb=1,且a+b>2.

(四川省成都華西中學 張云華 610051)

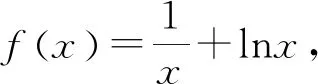
則當x=1時,f′(x)=0,當01時,f′(x)>0,

得f(x)在區間(0,1)上為減函數,在(1,+∞)上為增函數,則f(x)≥f(1)=1.

由m>1可知函數y=f(x)圖象與函數y=m圖象有兩個相異交點,

即關于x的方程f(x)=m有相異二實根,

即存在相異正數a,b,使f(a)=f(b)=m,

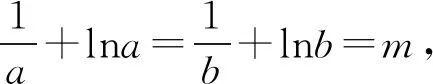
即am-alna=bm-blnb=1.

故存在相異正數a,b,

使am-alna=bm-blnb=1.

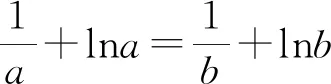
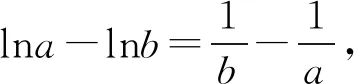
不妨設a>b>0，

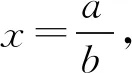
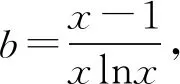
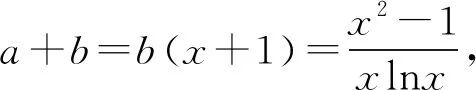
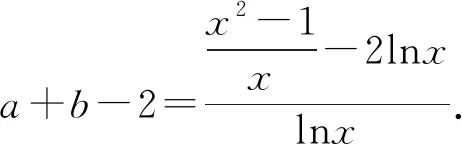
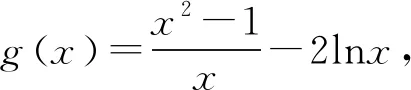
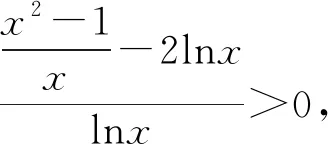
2549如圖1，△ABC中的邊AC與BC不等，其內切圓I與△ABC的邊BC、CA、AB切于點D、E、F,邊AB的中點為M,.直線DE與△ABC的外接圓O交于點H、G,證明：H、F、M、G四點共圓.

(安徽省旌德中學 趙忠華 242600)

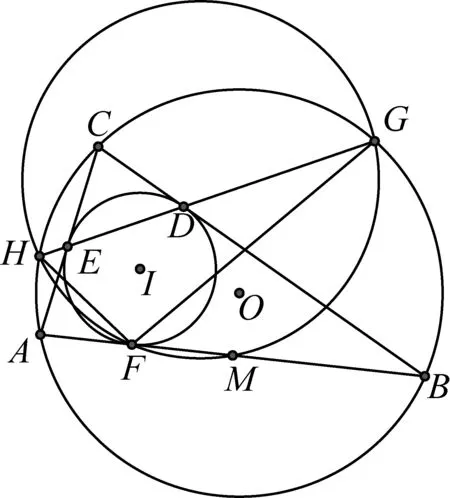
圖1

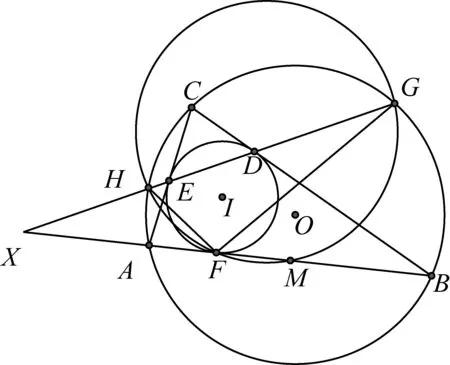
圖2

證明如圖2，因為AC≠BC,

所以DE與AB不平行，

設直線DE與直線BA交于點X,

由圓I為△ABC的內切圓得

AE=AF,BF=BD,CD=CE.

從而XA·BF=XB·AF,

即XA·(XB-XF)=XB·(XF-XA),

即2XA·XB=(XA+XB)·XF=2XM·XF,

得XM·XF=XA·XB=XH·XG.

于是H、F、M、G四點共圓.

2550 設△ABC的三邊長、三個內角平分線長、半周長及面積分別為a,b,c,wa,wb,wc,p,Δ,且∑為三元循環和,求證：

(1)

(天津水運高級技工學校 黃兆麟 300456)

證明由內角平分線長公式

立得

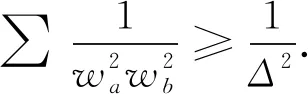
(2)

另一方面由

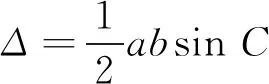
代入(2)式整理立得(1).

2020年7月號問題

(來稿請注明出處——編者)

2551 設△ABC的面積為S,證明：

(華中師范大學 國家數字化學習工程技術研究中心 彭翕成 曹洪洋 430079)

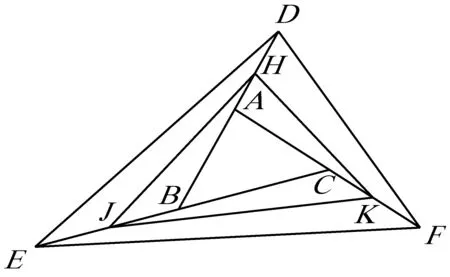
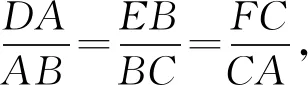
(江蘇省溧陽市光華高級中學 錢德全 213300;江蘇省溧陽市永平小學 張曉蔚 213333)

2553在銳角△ABC中，求證：

2cosAcosB+2cosBcosC+2cosCcosA

≤4cosAcosBcosC+1≤cosA+cosB+cosC.

(安徽省樅陽縣宏實中學 江保兵 246700)

2554已知⊙O為△ABC的外接圓，⊙Ia為∠BAC內的旁切圓，∠A的外角平分線交⊙O于點P，直線PIa交⊙O于點T,⊙Ia切BC于點D,切AB的延長線于點E.求證……