再探《數學通報》2268題

劉 鵬 楊光偉

(浙江師范大學教師教育學院 321004)

1 問題呈現(xiàn)

《數學通報》2015年10月號問題2268:

試證明:等式1

(1)

對于該問題,供題者柳冉在《數學通報》2015年第11期“2015年10月號問題解答”[1]中反復利用正弦、余弦的積化和差等公式及一定的運算技巧給出了證明.

其次,黃盛清老師在《數學通報》2017年第6期《基于余弦7倍角公式求幾個一元三次方程的解及其應用》[2]一文中通過余弦多倍角公式和方程的關系給出了證明.

筆者認為,此命題結論結構優(yōu)美,在閱讀過程中思考能否簡化其證明的同時,也有其它發(fā)現(xiàn).

2 嘗試簡證

文獻[2]有結論如下:

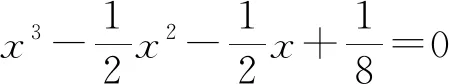
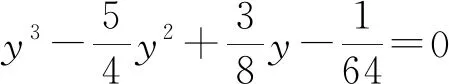
以上兩結論是從余弦7倍角出發(fā),給出了一個一元七次方程的解,分解一元七次方程進而得到幾個一元三次方程的解.最終根據一元三次方程3個根與系數的關系證明式(1).筆者在探索過程中,發(fā)現(xiàn)由結論1推出結論2的證明過程可以簡化許多,本文給出結論2的證明如下.

證明將結論1的方程

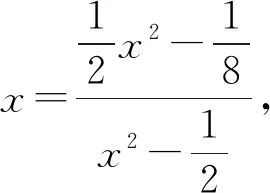
(2)

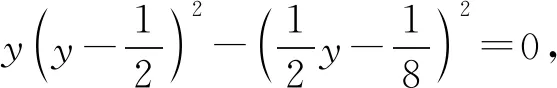
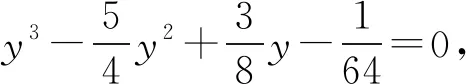
(3)

根據代換x2=y可知式(3)的解為

由此,結論2證畢.

進而證明式(1),根據式(3),令y=1-u,得

根據一元三次方程3個根與系數的關系,得

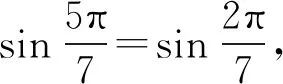
得等式1

可見,根據x巧妙的自身代換,將黃盛清老師的部分證明過程簡化許多.并且,在探究過程中,也有新的發(fā)現(xiàn).

3 探究發(fā)現(xiàn)

在思考過程中發(fā)現(xiàn),將式(2)先變形為

再變形為

(4)

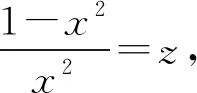
又因為式(3)的證明過程中令x2=y,故

將式(3)直接變形為

z3-21z2+35z-7=0,

(5)

由結論2知式(5)的解為

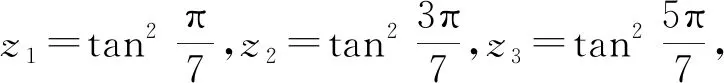
由此,得到結論3.

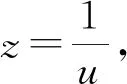
-7u3+35u2-21u+1=0.

(6)

由式(5)知式(6)的解為

由此,得到結論4.

受等式1的啟發(fā),由結論2根據一元三次方程3個根與系數的關系,得

(7)

同理,由……