一道中考題的思考

李瓊?cè)A

一、題目呈現(xiàn)

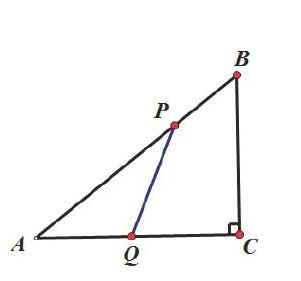
已知：如圖，在 中，∠C=900，AC=4cm，BC=3cm，點(diǎn) 由 出發(fā)沿 方向向點(diǎn) 勻速運(yùn)動(dòng)，速度為1cm/s;點(diǎn) 由 出發(fā)沿 方向向點(diǎn) 勻速運(yùn)動(dòng)，速度為2cm/s;連接 .若設(shè)運(yùn)動(dòng)的時(shí)間為 （0?t?2），解答下列問題：

（1）當(dāng) 為何值時(shí)，

（2）當(dāng)t為何值時(shí)，△APQ是等腰三角形？

二、題意分析

1.已知條件：（1）△ABC為直角三角形，且兩直角邊的長(zhǎng)度分別是3cm和4cm，可以聯(lián)想到勾股定理，從而求出AB=5cm;（2）知道點(diǎn)P、Q的運(yùn)動(dòng)方向和速度，當(dāng)時(shí)間為t秒時(shí)，可以表示線段AQ=2tcm，BP=tcm，進(jìn)一步得到AP=（5-t）cm。

2.所求問題：（1）當(dāng)t為何值時(shí)， ？

（2）當(dāng)t為何值時(shí)，△APQ是等腰三角形？

三、題目解析

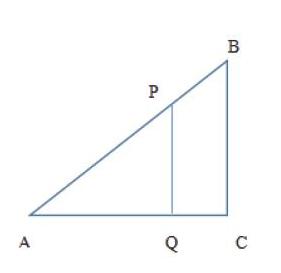
（1）要滿足PQ∥BC，學(xué)生可能會(huì)想到“角—平行”或“相似—平行”（即邊的關(guān)系解決平行），但從已知條件分析，點(diǎn)的運(yùn)動(dòng)轉(zhuǎn)化后是線段的長(zhǎng)度，所以從邊的角度思考到線平行，那么通過三角形的相似可以實(shí)現(xiàn)。

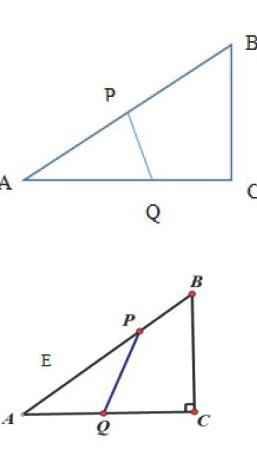
（2）這個(gè)問題的難度明顯增加，主要考查學(xué)生思維的全面性。要使△APQ是等腰三角形，要分情況考慮：因?yàn)镻、Q兩點(diǎn)是運(yùn)動(dòng)的，而點(diǎn)A卻是一定點(diǎn)，那么思考時(shí)，將“動(dòng)”轉(zhuǎn)為“靜”，以“靜”制“動(dòng)”，所以考慮以A為頂角頂點(diǎn)時(shí)、以A為底角頂點(diǎn)時(shí)兩個(gè)方面，即當(dāng)AP=AQ時(shí);當(dāng)QA=QP時(shí);當(dāng)PA=PQ時(shí)。

①若點(diǎn)A為頂角頂點(diǎn)即當(dāng)AP=AQ時(shí)

四、思想方法總結(jié)提煉

1.通過此題解決，總結(jié)得出動(dòng)點(diǎn)問題體現(xiàn)了以下數(shù)學(xué)思想：分類討論思想、數(shù)形結(jié)合思想、轉(zhuǎn)化思想、函數(shù)思想、方程思想等;

2.解題思路：“動(dòng)”中求“靜”? ? ?化“動(dòng)”為“靜”? ?以“靜”制“動(dòng)”（在變化中找到不變的性質(zhì)是解決數(shù)學(xué)“動(dòng)點(diǎn)”探究題的基本思路，這也是動(dòng)態(tài)幾何數(shù)學(xué)問題中最核心的數(shù)學(xué)本質(zhì)）。

3.解題步驟：審（讀題目、找條件、分析運(yùn)動(dòng)變化的形式及過程，思考運(yùn)動(dòng)初始狀態(tài)時(shí)幾何元素的關(guān)系，確定可以求出的量）;

定（確定動(dòng)點(diǎn)位置，畫出符合題意的圖形，尋找定點(diǎn)，化動(dòng)為靜）;

寫（根據(jù)條件，將動(dòng)點(diǎn)的移動(dòng)距離以及解決問題時(shí)所需的條件用含t的代數(shù)式寫出來）;

列（利用特殊圖形的性質(zhì)或相互關(guān)系，尋找等量列出方程或函數(shù)關(guān)系求解問題）

分類（分析特殊圖形的性質(zhì)，考慮是否要分情況討論）

五、題目拓展延伸

（1）當(dāng) 為何值時(shí)，以A、P、Q為頂點(diǎn)的三角形與△ABC相似？

（2）如圖①，設(shè)ΔAQP的面積為y（cm2），求y與t之間的函數(shù)關(guān)系式;（在點(diǎn)P、Q運(yùn)動(dòng)過程中，ΔAQP的形狀和大小都會(huì)發(fā)生變化，那么它的面積會(huì)發(fā)生著怎樣的變化呢？能否建立面積與t之間的變化關(guān)系式呢？引導(dǎo)學(xué)生將問題再次改變）

（3）如圖②，連接PC，并把ΔPQC沿QC翻折，得到四邊形PQP/C，那么是否存在某一時(shí)刻t，使四邊形PQP/C為菱形？若存在，求出此時(shí)t的值;若不存在，說明理由。

用總結(jié)的方法解決逐級(jí)變式延伸的題目，達(dá)到舉一反三的目的，實(shí)現(xiàn)“一道通一類”！