一題多解 拓展思維

陳俐青

[摘? 要] 一題多解的教學方法，能反映學生對數學知識掌握的程度，又能考查學生的思維靈活度. 縱觀初中數學中考試題，有不少是一題多解的題型. 因此，教師在日常課堂教學中，應關注習題或例題的一題多解教學，通過問題情境的設置或題型的轉換，整合交匯各個知識點，讓題目充滿靈動與智慧，以激發學生自主學習的欲望，從而拓展思維能力.

[關鍵詞] 一題多解;思維;證明

數學學習固然離不開解決問題，而解決問題的關鍵在于緊扣問題的核心，捕捉到問題中有用的數學信息，結合學生已有的認知結構進行分析，獲得解題方法，這是優化學生認知結構，提高解題能力，培養數學思維的過程. 特別是一些看似復雜的問題，卻有多種解決方法，教師要引導學生發現問題的特征，尋找解題的突破口，根據數學模型，逐層深入、循序漸進地進行解題，以培養學生的思維能力. 本文筆者結合一道一題多解的證明案例，進行拓展分析，談談如何在一道題中巧妙地運用數學思想，激發學生學習的內驅力，以提升其思維能力.

問題? 如圖1，點O在線段AB上，AO=2，OB=1，OC為射線，且∠BOC=60°，動點P以每秒2個單位長度的速度從點O出發，沿射線OC做勻速運動，若運動時間是t秒.

（1）當t=■秒時，則OP=________，S■=________;

（2）當△ABP是直角三角形時，求t的值;

（3）如圖2，當AP=AB時，過點A作AQ∥BP，并使得∠QOP=∠B，求證：AQ·BP=3.

分析：本題題干簡潔明了，結構合理，圖像清楚，內涵較豐富，問題的梯度也一目了然，是一道集知識與思想于一體的運動綜合題.

第（1）問的起點比較低，當t=■秒時，則OP=1，S■=■.

第（2）問把方程思想和分類討論思想融于一體，當△ABP為直角三角形的時候，①因為∠A<∠BOC=60°，所以∠A不會是直角;②若∠ABP=90°，則t=■=■=1;③若∠APB=90°，容易求得t=■.

第（3）問的解題入口比較寬，解題方法也有多種，但這一問對學生思維的廣度和深度提出了較高的要求，也是壓軸題區分學生水平能力的典型表現. 在解題時，可捕捉結論中的數學信息，以確定思維的方向，將問題中的數量關系轉化為幾何的關系，實現條件與結論的互相交流.

隱含信息：待證明的結論AQ·BP=3可轉化成比例式■=■，通過包含線段AQ與長度為3的線段的三角形，與包含線段BP與長度為1的線段的三角形相似而對應的線段成比例來獲得隱藏信息.

證法1? 連接PQ，設AP與OQ相交與點F（如圖3）.

因為AQ∥BP，所以∠QAP=∠APB，因為AP=AB，所以∠APB=∠B，所以∠QAP=∠B. 又∠QOP=∠B，所以∠QAP=∠QOP，因為∠QFA=∠PFO，所以△QFA∽△PFO，故■=■，即■=■. 又∠PFQ=∠OFA，所以△PFQ∽△OFA，∠3=∠1. 因為∠AOC=∠2+∠B=∠1+∠QOP，又∠B=∠QOP，所以∠1=∠2，故∠2=∠3，可得△APQ∽△BPO，■=■，所以AQ·BP=AP·BO=3×1=3.

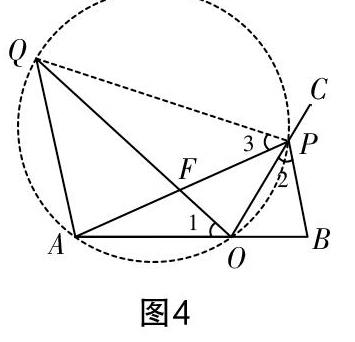
證法2? 連接PQ（如圖4）.

同上可證∠QAP=∠QOP. 所以Q，A，O，P四點同圓，有∠3=∠1. 同上可證∠2=∠3，所以△APQ∽△BPO，■=■，所以AQ·BP=AP·BO=3×1=3.

隱含信息：結論AQ·BP=3還可轉化成比例式■=■，即可通過含有線段AQ與長度為2的線段的三角形和含有線段BP與長度為■的線段的三角形相似的對應線段成比例獲得.

證法3? 過點B作BE∥AP交PO的延長線于點E（如圖5）.

易知有△APO∽△BEO，所以■=■=■，因為AP=AB=3，所以BE=■. 同上可證∠AOQ=∠OPB，又∠QAO+∠OBP=180°，∠EBP+∠APB=180°，∠OBP=∠APB，所以∠QAO=∠EBP，故△QAO∽△EBP，■=■，即AQ·BP=BE·AO=■×2=3.

證法4? 過點B作BE∥OP交AP的延長線于點E（如圖6）.

則有■=■=■，因為AP=AB=3，所以PE=■，同上可證：∠AOQ=∠OPB，因為BE∥OP，所以∠EBP=∠OPB，∠AOQ=∠EBP. 又∠QAO+∠OBP=180°，∠EPB+∠APB=180°，∠OBP=∠APB，所以∠QAO=∠EPB，故有△QAO∽△EPB，■=■，即AQ·BP=PE·AO=■×2=3.

隱含信息：結論AQ·BP=3又可以轉化成比例式■=■，根據以上證明思路，構造相似三角形而獲得求證.

關于線段的乘積問題，最常用的解題方法就是確定好位置以后尋找相似，怎樣根據已有條件作出合理的輔助線，找出相似三角形是本題的解題突破口. 上述幾種解題思路是常用的解題思路，雖然解法不一樣，但都是以AQ·BP=3的隱含信息作為解題思路的出發點，找到解決問題的突破口，即相似三角形，即可論證. 當然，本題還有其他論證方法，筆者不再一一贅述.

實踐證明，解題方法越多，對思維水平的要求越高. 有高度活躍的數學思維才能有開闊的解題思路，學生運用自己的知識結構，突破條條框框的約束，用發散性思維探索出多種解題辦法，既鍛煉了解題能力，又刺激了思維的發展. 因此，教師應在適當的時候，給予學生充分的肯定與鼓勵，這樣有助于讓學生對數學學科產生濃厚的學習興趣，能在培養學生思維能力的同時有效地提升數學核心素養.