基于試題診斷的高三數學教學實踐
王世朋

高三二輪數學復習是以提升學生解題能力、完善學生思維品質為主要目的。如何使復習更精準,是高三教師必須思考的問題,也是有意義的研究課題。筆者基于課堂教學中的實踐案例分析,強化試題診斷功能,借此提升復習的精準度。
一、基于試題診斷的案例分析
為了有效完善解析幾何中直線與拋物線綜合問題解題策略,筆者重點選擇了合肥市2017年二模(文)第20題進行教學診斷與講評后反思。
試題:已知拋物線E∶y2=2px(p>0)與圓
O∶x2+y2=8相交于A,B兩點,且點A的橫坐標為2,過劣弧AB上動點P(x0,y0)作圓O的切線交拋物線E于C,D兩點,分別以C,D為切點作拋物線E的切線l1,l2,l1與l2相交于點M。
求拋物線E的方程;
求點M到直線CD距離的最大值。
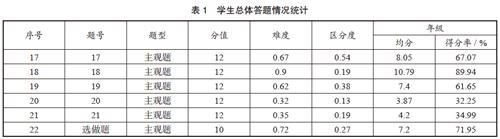
學生總體答題情況統計:
閱卷統計結果顯示,本題實際得分明顯低于其他解答題(見表1),說明學生答題障礙很大,值得去進行教學思考和研究。通過答題明細可以看出,絕大部分學生僅完成了第一問的解答。這里有意遴選了兩位得分較高的學生答題原卷,不難看出這兩位同學解題路徑基本明確,運算求解能力仍需提升,尤其是對解題關鍵點的突破還要強化理解。
二、試題診斷基本路徑分析
通過此問題的分析與解答,不難提取出以下基本知識點。如點與曲線方程關系、劣弧的概念、過圓上一點的切線方程求法、過拋物線上一點的切線方程求法、兩直線的交點、點到直線距離、圓的方程和拋物線方程。作為一道題所涵蓋的知識點已經足夠多了,如果學生基本功不扎實,有知識混淆點或盲點,問題也就無法有效解答。通過以上知識點的梳理,我們可以很清楚地幫助學生梳理教材知識點,回顧知識發生、發展的過程,助力形成堅固的知識體系和脈絡。
1.診斷基本解題方法
通過知識點的回顧,就需要我們提出解題的策略,尤其是可執行的具體方案。通過問題的條件分析,我們可以清晰地知道解題路徑為:利用點坐標求拋物線方程求直線方程,并設C,D坐標
求出l1,l2方程求出點坐標計算點到直線距離轉化為函數問題求解最值。為了解題的順利進行,需要進一步明確方法求直線方程、求點坐標和函數最值。
2.診斷學生思維過程
通過解法的提出,在實際中需要執行運算,確保為下一步的執行提供準確、可靠的數據結果。通過答題過程就能有效監測一個學生的思維品質好壞,如動點P(x0,y0)作圓O的切線,切線方程的求法與表示,如果選擇設點斜式切線方程,則要考慮斜率是否存在,如果能理解過圓上一點的切線方程一般形式,則解題步長就減少了很多。在C,D點坐標的設法上如果沿用橢圓常規設法,會給后面l1,l2寫法帶來不便,而選擇拋物線上點的常用設法,會讓后面M點坐標計算得到簡便。在點M到直線CD距離最值求解上,本著函數思想為原則,點M坐標的簡化就顯得尤為重要。以上這些問題處理的策略,代表的是學生答題的數學思維水平高低,如果能有效選擇形式,某種程度上可以反映學生的思維能力高低。
三、基于試題診斷的教學策略分析
解析幾何模塊的復習常被師生視為較難啃的“骨頭”,選填注重“小靈活”,大題注重“大融合”。對于學生來說,需要積累有效的解題活動經驗,提升解題素養。對于教師來說,復習中要強化訓練的總結與整理,授之以漁是關鍵。
第一,厘清解題路徑。從近年來的高考真題和地方模考試題中可以看出,解析幾何題往往需要結合圖形進行分析解答。教學中需要強化把文字條件和圖形語言進行緊密聯系,最終把問題放入圖形中,充分發揮幾何直觀和數學抽象功能,找到明確可行的解題路徑。
第二,攻克解題要點。有了路徑的指引后,需要強化學生關鍵點的計算。本題解決的第一個關鍵點是直線方程的計算,實施運算中要考慮直線可以垂直于軸,避免設點斜式時出現不嚴謹的情況。本題解決的第二個計算要點是切線的計算,設,,切線:,代入得,由解得,方程為,同理
方程為。第三個解題要點是點坐標求解,聯立,解得,又方程為,其中,滿足,,聯立方程得,則,∴M(x,y)滿足,即點
為。最后一個運算要點是點到直線距離。點到直線:的距離關于單調減,故當且僅當時,。只有解題中準確把握了解題關鍵點,借以學生良好的數學運算和數據處理能力,問題才能真正地得到解決。
第三,聚焦解題思想。最終要解決的問題是最值問題,因為P(x0,y0)在動,所以要建立函數模型,又考慮到點在直線上或點圓上動,所以可以建立關于的一元函數模型,進一步由題知自變量。要得到x0∈[2,2]最終的函數表達式需要通過點
到直線距離公式獲得,這就需要我們計算點坐標和直線方程,難點自然就是計算出l1,l2方程并聯立才能得到點坐標,并選擇用變量x0,y0來表示坐標最理想。
四、借助試題診斷提升復習精準性的幾點思考
美國數學家哈爾莫斯說:“數學的真正組成部分應該是問題和解。”通過解題教學促進學生深度思考,積極體驗問題解決的思維過程,反思建構問題解決的活動經驗。筆者認為,通過試題診斷開展探究教學,助力復習精準性提升應落實好以下幾個環節。
第一,對比答題情況,判斷試題講解的價值。提出問題有時比解決問題更有價值,尤其是緊張的高三二輪復習中,好的問題一定可以助力復習的效率提升。通過前面綜合分析,為了復習解析幾何中圓與直線、直線與拋物線相關位置關系運算的掌握情況,選擇了一道知識點容量較大的綜合題,通過問題答題的基本情況對比,可以診斷學生的基本數學素養,也能洞察學生的思維發展水平,實現試題的選拔功能。總之,問題選擇要具有很強的導向性,研究的問題選擇很有代表性,則復習的精準性就能有了一定的保障,復習效率也會有顯著提升。
第二,對比得分情況,定位試題講解程度。通過答題情況對比,尤其是得分情況對比,很容易診斷學生對問題的理解程度,有助于教師對學情的準確把握。基于得分情況的分析,能夠進一步反映學生對知識的理解、問題解決程度的刻畫,如果在實際教學中能對已選問題很好地進行解析和判斷,能深入挖掘問題解決過程中所蘊含的知識、公式、原理與思想,勢必也會提高復習質量,助力學生的個性化發展。
第三,對比不同答題方法,診斷學生思維品質。雖然我們用心選好了問題,也事先備好了所有可能的解題路徑,如果問題和策略不適合學生已有的學情,結果也一定不會讓我們滿意,所以有效開展課堂探究,分析不同解法學生所燃放的思維品質是非常重要的舉措。尤其是緊張的高三課堂學習,每一節課都很重要,如果教師能基于學情進行教學設計和診斷,凝練問題解決的基本途徑,相信對學生走出題海戰術,提升學科素養大有裨益,也會助力師生良好關系的建立,助力學生良好思維品質的養成。
第四,對比不同答題程度,診斷學生意志品質。作為高三二輪復習,我們更多的是為學生提供學習的載體和引領,讓學生們在探究中體驗和深化對知識的理解與方法的應用,更重要的是訓練和培養學生解題的能力和經驗。經驗需要經常總結才有效,經常使用才有用,所以進行探究訓練后的總結是為我們積累經驗的必備步驟。通過對不同答題程度的評判,能有助于準確診斷學生的意志品質,估計學生的學科潛力,預判學生的學習能力。
高考試題具有八大功能:測評選拔功能、科研選題功能、命題示范功能、知識延展功能、思維訓練功能、數學思想滲透功能、教學導向功能與德育滲透功能。作為一線教師來說,強化對試題功能性的針對性訓練與指導,提升學生綜合解題能力是關鍵。
本文系2019年安徽省教育信息技術研究課題“基于教育大數據的高中數學學情診斷與精準教學的行動研究”(課題編號:AH2019048)的階段性成果。
(作者單位:安徽省合肥市第七中學)
責任編輯:李莎
lis@zgjszz.cn

