一只螞蟻的思考

謝 川

（重慶市長征學校 重慶 400080）

近幾年“最值問題”在中考中頻繁出現，形式多樣，主要綜合了幾何和函數兩大部分的知識，難度較大。但通過探索研究會發現最值問題其實都可以轉化為三大類的問題，一是二次函數配方求最值；二是轉化為兩點之間線段最短問題；三是垂線段最短問題。大家經常遇到的“胡不歸模型”則可轉化為垂線段最短，“阿氏圓模型”則可轉化為兩定點之間的路徑問題。那么對于題目中說到的勾股定理里面的最值則主要是兩點之間線段最短問題。

勾股定理具有獨特的魅力，它是一個基本幾何定理，勾股定理反映了直角三角形中三邊之間的數量關系，從邊的角度進一步刻畫了直角三角形的特征，它可以解決許多直角三角形中的計算和證明問題，同時也在我們的實際生活中發揮著重要作用，是人類早期發現并證明的重要數學定理之一，用代數思想解決幾何問題的最重要的工具之一，也是數形結合的紐帶之一，所以它更是初中數學中一個重要的知識內容。

對于北師版教材來講，《勾股定理》屬于八年級上冊第一章的內容，當我們學完勾股定理及其逆定理后，會進入到勾股定理的應用部分，課本上這一部分主要是探究螞蟻在各種幾何體上要吃到食物如何選擇最短路徑的問題，涉及的幾何體主要有圓柱、正方體、長方體、臺階等常見的幾何體，用到的解決方法通常是把幾何體側面展開，把立體圖形問題轉化為熟悉的平面圖形問題，也就是運用“化曲為平”或“化折為直”的思想來解決問題。而現在要闡述的就是關于勾股定理應用這一節里我對于一個問題的思考。

在這堂課開始之前，我已經上過一次勾股定理的應用了，所以上課之前簡單的備了一下課，胸有成竹的進入課堂，開啟我自認為一切都會在掌握之中的課堂。

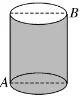
“同學們，請看到課本引例，A處的螞蟻要想吃到B處的食物，它應該怎樣走呢？”學生都能夠想到各種各樣的路徑?！澳钦垎栐鯓幼卟攀亲罱哪?？”學生思考片刻，再加上我的實物演示及分析引導，基本上都掌握了找最短路徑的方法，即是把圓柱側面展開成一個長方形，在展開的平面圖上確定螞蟻和食物的位置，再利用兩點之間線段最短畫出路徑，最后用勾股定理來解答。自認為講解效果很好的我正準備進入下一個環節，一個學生打斷了我：“老師，這種展開方式算出來的結果就一定是最短的嗎？螞蟻直接從A點垂直朝上走，然后沿圓柱的直徑走到B就不能最短嗎？”我愣了一下，不過我立馬解釋道：“那我們可以一起來計算一下這種路徑的結果，比較一下這兩種路徑的結果?！弊罱K在兩個數據的有力說明下，這位同學若有所思的點點頭，作為老師的我總算松了一口氣，繼續進行我的教學。

等到我下一次上課，我把所想的這個問題放在課堂上和同學們一起計算和探討，這個結果讓班上有疑惑的同學恍然大悟，也讓同學們對這個模型認識得更全面，同時也讓我對這個問題有了新的認識。但是要知道的是這個思考的結果只針對螞蟻和食物的位置如引例所給的相對位置，一旦位置發生變化，那以上的結論顯然不成立，至于在其它模型里面是否也有特殊的情況呢，大家可以再進行思考。

雖然這種有關勾股定理的最值在我們的中考試題中一般沒有出現，但是對于學習知識來講，我們不是為了應試而學習，多發現問題，思考問題，解決問題可以培養我們的思維能力。多思多問會讓我們一身受益，所以任何一個出現的問題都值得我們去研究思考。

通過對這一問題的分析思考給了我兩點啟示：一方面，我明確的知道在課堂教學當中，作為教師要經常鼓勵學生提出問題，思考問題，抓住每一次鍛煉思維和培養興趣的機會，體現學數學的本質。另一方面，作為一名教師，應該多進行教學反思，教學反思對教師自身教學水平的提高，以及對教學效果的提高都有舉足輕重的作用。思考與反思是教師進步的階梯，是教師進步的重要途徑。