基于核心素養的解三角形模型例探*

王瑞生

廣東省惠州市惠陽區崇雅實驗學校 (516213)

解三角形是高考必考知識點，從歷年高考試題分析可知，其難度適中，考查知識點較為綜合，求解入手容易但數學運算能力、邏輯推理能力要求較高，以致很多學生在解題過程中出現“會做不得分”的現象.為此，我們要對典型高考題、常考模擬題等進行分析總結，發現規律，掌握某一類問題的解題方法，以至事半功倍.

引例1 (2013年高考數學全國新課標卷Ⅱ理科第17題)ΔABC中，內角A,B,C的對邊分別為a,b,c，已知a=bcosC+csinB．

(Ⅰ)求B，(Ⅱ)若b=2,求△ABC面積的最大值.

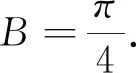
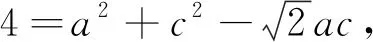
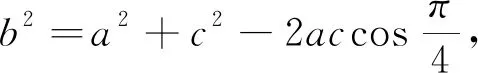
方法二：在ΔABC中，由正弦定理得a=

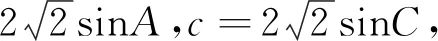
反思：(1)余弦定理b2=a2+c2-2accosB是三角形三條邊長和一個內角的等量關系式，可變形為b2=(a+c)2-2ac(1+cosB).當已知b和B時，余弦定理可以看作a+c和ac的等量關系式，結合基本不等式,可分別探求a+c和ac的最值問題.

(3)已知三角形的一邊及其對角，求該三角形面積的最大值.這類問題的解題思路有以下模型1：

在ΔABC中，已知內角A及其所對的邊長為a.

求(1)AB+AC的最小值；(2)AB·AC的最大值.

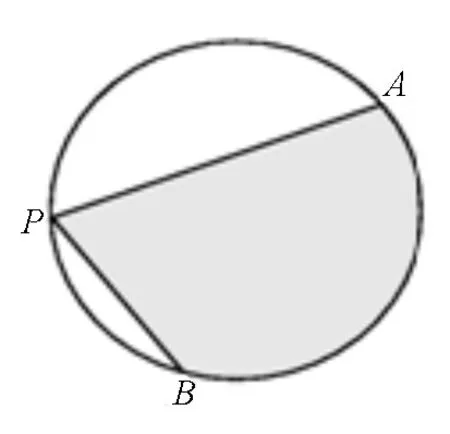
圖1

高考題再現：(2019年高考數學北京卷文科第8題)如圖1,A、B是半徑為2的圓周上的定點,P為圓周上的動點,∠APB是銳角,大小為β.圖中陰影區域的面積的最大值為( ).

A.4β+4cosβ

B.4β+4sinβ

C.2β+2cosβD.2β+2sinβ

思路探求：本題靈活考查學生直觀想象、數據分析等數學核心素養.

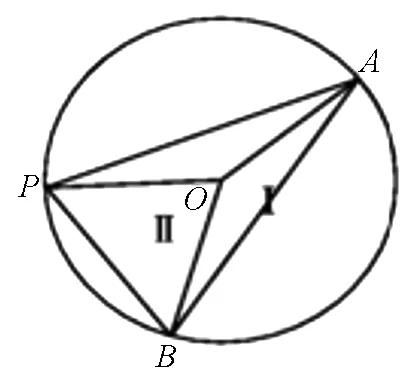
圖2

如圖2,設該圓心為點O,連接OA、OB,半徑r=2,∠AOB=2∠APB=2β,陰影部分Ⅰ(扇形)的面積S1=βr2=4β為定值,SΔOAB=

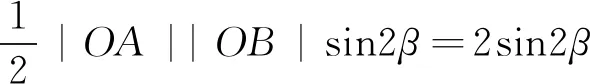
在ΔOAB中可得AB=4sinβ，問題轉化為已知ΔPAB的一條邊AB及其對角∠APB，求另兩邊PA·PB的最大值.利用模型1的解題方法可得正確答案為B.

引例2 (2015年高考數學全國新課標卷Ⅱ理科第17題)△ABC中，D是BC上的點，AD平分∠BAC，△ABD是△ADC面積的2倍.

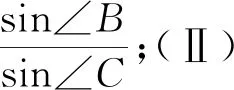
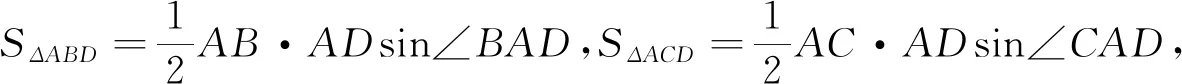
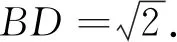
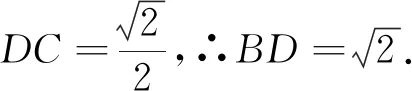
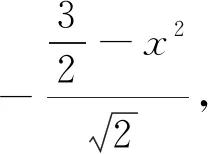
反思：(1)余弦定理具有將三角形的三條邊和一個內角建立等量關系式的重要功能.

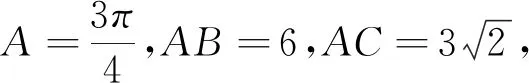
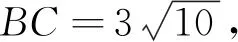
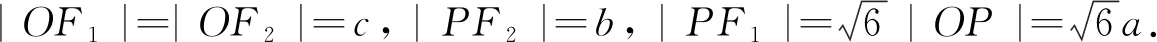
(3)條件線段和待求線段組成以一對鄰補角α、β分別作為一個內角的兩個三角形的三條邊時，結合余弦定理，建立方程cosα+cosβ=0可解三角形.即有以下模型2:

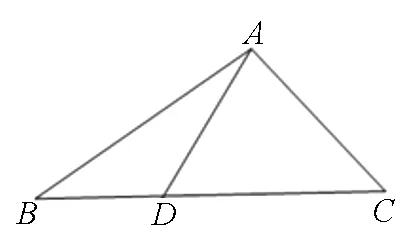
圖3

如圖3，在ΔABC中，線段AB、BD、AD、CD、AC組成以∠ADB與∠ADC為一對鄰補角的兩個三角形，由cos∠ADB+cos∠ADC=0，結合余弦定理可解三角形.

高考題再現：(2019年高考數學全國新課標卷Ⅰ理科第10題)已知橢圓C的焦點為F1(-1,0)，F2(1,0)，過F2的直線與C交于A，B兩點.若│AF2│=2│F2B│，│AB│=│BF1│，則C的方程為( ).

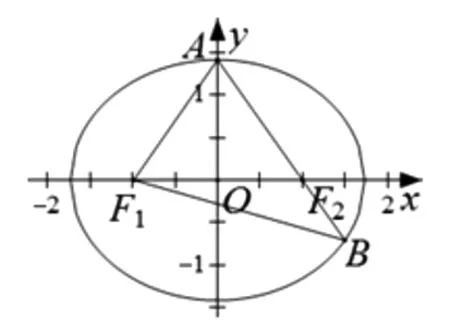
圖4

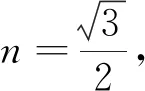
教學感悟:數學核心素養下的解三角形問題應重視數學學科觀念、規律探索，注重數學思想方法的滲透和考查.高考試題在解三角形問題中常考利用公式或公式的變形直接求值，分析正弦定理、余弦定理的結構特征與題設條件的關系，特別是三角形的邊角聯系，精準選用公式及變換的方向，體培養學生的直觀想象、邏輯推理、數學運算和數據分析等核心素養.