運(yùn)用圖示，延展學(xué)生在數(shù)學(xué)實(shí)驗(yàn)中的思維深度

林超

[摘要]圖示能突顯題干中關(guān)鍵信息之間的相互關(guān)系，數(shù)學(xué)實(shí)驗(yàn)?zāi)艽龠M(jìn)靜態(tài)數(shù)學(xué)與動(dòng)態(tài)數(shù)學(xué)的融通，在數(shù)學(xué)實(shí)驗(yàn)中運(yùn)用圖示，是期望運(yùn)用動(dòng)態(tài)的圖示建構(gòu)實(shí)驗(yàn)的思維網(wǎng)絡(luò)，使學(xué)生體驗(yàn)到數(shù)學(xué)學(xué)習(xí)的完整與活力。在教學(xué)中，教師可以通過(guò)“雙氣泡圖”“流程圖”“樹(shù)形圖”這三種圖示來(lái)明確實(shí)驗(yàn)教學(xué)環(huán)節(jié)間的互動(dòng)關(guān)系，在整合認(rèn)知系統(tǒng)、激發(fā)類(lèi)比思維的同時(shí)，實(shí)現(xiàn)思維的深度延展。

[關(guān)鍵詞]圖示;數(shù)學(xué)實(shí)驗(yàn);思維深度

[中圖分類(lèi)號(hào)]G623.5

[文獻(xiàn)標(biāo)識(shí)碼]A

[文章編號(hào)] 1007-9068（ 2020） 29-0027-04

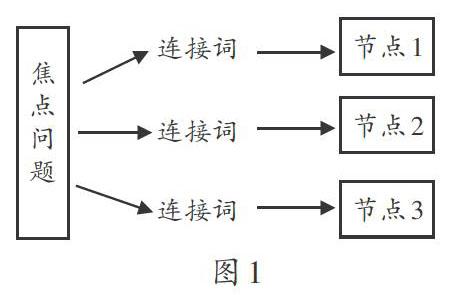
美國(guó)教育心理學(xué)家諾瓦克教授開(kāi)發(fā)出作為學(xué)習(xí)腳手架的“概念圖”，即利用圖示的方法把人腦中的概念、思想與理論可視化，從而便于人們的思考、交流與表達(dá)。運(yùn)用時(shí)，只需簡(jiǎn)單的方框（圓圈）和連線(xiàn)就能表示復(fù)雜的概念間的關(guān)系（如圖1），同時(shí)還可以根據(jù)學(xué)習(xí)的需要，在原有的概念關(guān)系間加入新的概念及關(guān)系。這種圖示法早已被廣泛運(yùn)用于數(shù)學(xué)學(xué)科，為學(xué)生學(xué)習(xí)數(shù)學(xué)知識(shí)提供了有力的支持。

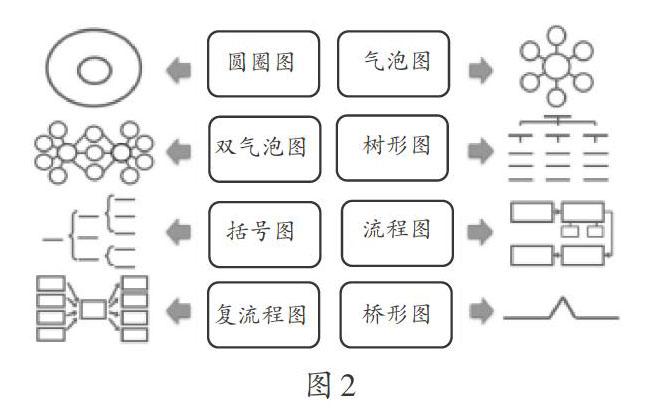
目前數(shù)學(xué)教學(xué)中所運(yùn)用的圖示，是綜合了多種思維方式的精確表示法，能突顯題干中關(guān)鍵信息之間的相互關(guān)系，激活舊知。美國(guó)教育學(xué)家海勒博士開(kāi)發(fā)出一組思維可視化工具“八大思維圖示法”（如圖2），因其每種圖示都對(duì)應(yīng)著一種具體的思維策略，豐富了學(xué)生解題的思路，延展了學(xué)生解題的深度，被數(shù)學(xué)教學(xué)廣泛采用。

郭慶松老師對(duì)小學(xué)數(shù)學(xué)實(shí)驗(yàn)的界定：在數(shù)學(xué)思想和數(shù)學(xué)教學(xué)理論的指導(dǎo)下，小學(xué)生借助實(shí)物和工具，通過(guò)對(duì)實(shí)驗(yàn)素材進(jìn)行“數(shù)學(xué)化”的操作來(lái)驗(yàn)證數(shù)學(xué)結(jié)論、建構(gòu)數(shù)學(xué)概念、探索數(shù)學(xué)規(guī)律、解決數(shù)學(xué)問(wèn)題的一種數(shù)學(xué)學(xué)習(xí)方式。這體現(xiàn)了數(shù)學(xué)實(shí)驗(yàn)注重實(shí)測(cè)與創(chuàng)思的特點(diǎn)，當(dāng)課堂與實(shí)驗(yàn)結(jié)合時(shí)，讓學(xué)生學(xué)會(huì)數(shù)學(xué)思考應(yīng)是數(shù)學(xué)實(shí)驗(yàn)的旨?xì)w，而將思維教學(xué)滲透于實(shí)驗(yàn)的每一個(gè)環(huán)節(jié)，圖示則是最有效的切人點(diǎn)。在數(shù)學(xué)實(shí)驗(yàn)中運(yùn)用圖示，正是基于其能夠表達(dá)實(shí)驗(yàn)環(huán)節(jié)之間的互動(dòng)關(guān)系，構(gòu)建學(xué)生走向深度思維的腳手架。下文以三種圖示為例，闡釋在數(shù)學(xué)實(shí)驗(yàn)中運(yùn)用圖示對(duì)學(xué)生思維深度的延展作用。

一、雙氣泡圖——在比較中搭建數(shù)學(xué)模型，激發(fā)思維碰撞

數(shù)學(xué)實(shí)驗(yàn)多是圍繞一個(gè)知識(shí)點(diǎn)的理解而展開(kāi)，因?yàn)榫劢裹c(diǎn)小，所以通過(guò)內(nèi)嵌于學(xué)習(xí)過(guò)程的實(shí)驗(yàn)可以直指對(duì)內(nèi)容的理解與問(wèn)題的求解。但正如弗洛登特爾所指，旁觀者確實(shí)可以將它解釋為數(shù)學(xué)，因?yàn)樗煜?shù)學(xué)，也了解實(shí)驗(yàn)過(guò)程中兒童的活動(dòng)是什么意思，可是兒童并不知道。這就意味著，數(shù)學(xué)實(shí)驗(yàn)在引導(dǎo)學(xué)生完整經(jīng)歷探索、發(fā)現(xiàn)規(guī)律的同時(shí)，還應(yīng)當(dāng)使學(xué)生也能明白這些實(shí)驗(yàn)的意義。而雙氣泡圖可將圖形與比較融為一體，搭建與學(xué)生思維相對(duì)應(yīng)的圖示，在構(gòu)圖、讀圖的過(guò)程中形成對(duì)應(yīng)的表象，最終清晰地傳達(dá)實(shí)驗(yàn)的意義。

例如，運(yùn)用雙氣泡圖可以將長(zhǎng)方體表面涂色問(wèn)題搭建在學(xué)生對(duì)正方體表面涂色的認(rèn)知基礎(chǔ)上。

根據(jù)“從簡(jiǎn)單想起”的策略，且學(xué)生已掌握正方體中涂色個(gè)數(shù)的計(jì)算方法，實(shí)驗(yàn)伊始，教師出示實(shí)驗(yàn)記錄單（如表1），并提出問(wèn)題：“如果不是正方體，而是長(zhǎng)方體，不同的涂色面數(shù)的小長(zhǎng)方體又會(huì)在哪？”學(xué)生會(huì)借助經(jīng)驗(yàn)提出猜想：“三面涂色的還是在頂點(diǎn)，兩面涂色的還是在棱的中間，一面涂色的肯定在面的中間，但計(jì)算方法不同。”此時(shí)，如果放手讓學(xué)生利用學(xué)具進(jìn)行驗(yàn)證，學(xué)生往往會(huì)只創(chuàng)造他們感興趣的模型進(jìn)行探討，得出的結(jié)論僅僅是問(wèn)題鏈上的一個(gè)點(diǎn)。其實(shí)，學(xué)生實(shí)驗(yàn)的意義并不是解決單一問(wèn)題，而是為了探究這一類(lèi)現(xiàn)象的本質(zhì)。為了使學(xué)生通過(guò)數(shù)學(xué)實(shí)驗(yàn)真正實(shí)現(xiàn)深度學(xué)習(xí)，真正激發(fā)思維碰撞，筆者繪制了圖3。

在圖3的引導(dǎo)下，學(xué)生迅速厘清思路，不再糾結(jié)于個(gè)人的喜好，而是聚焦于長(zhǎng)方體和正方體的共同特征“面、棱、頂點(diǎn)”上。很快，就有小組提出了新發(fā)現(xiàn)，并展示了本組的圖示（如圖4）。這個(gè)小組的匯報(bào)剛剛結(jié)束，立刻又有小組提出了新發(fā)現(xiàn)：“他們研究的是長(zhǎng)、寬、高都超過(guò)兩層（a>2，b>2，c>2）的長(zhǎng)方體，如果長(zhǎng)方體的長(zhǎng)、寬、高中出現(xiàn)一層或是兩層，這個(gè)結(jié)果就不對(duì)了，特別是一層的，里面還可能出現(xiàn)四、五面涂色的小長(zhǎng)方體。因此，我們把圖示的右邊作了修改（如圖5）。”

研究到此，學(xué)生發(fā)現(xiàn)當(dāng)長(zhǎng)方體的長(zhǎng)、寬、高中的出現(xiàn)一層時(shí)，一面涂色的小長(zhǎng)方體就沒(méi)有了，兩面涂色的小長(zhǎng)方體也不在棱上……筆者認(rèn)為這次關(guān)于“雙氣泡圖”的嘗試，充分體現(xiàn)了其在兩個(gè)比較對(duì)象間“尋找相似與不同”的思維策略。同時(shí)也暴露出由于兩個(gè)比較對(duì)象間有大量的相似與不同，因此不能簡(jiǎn)單地等同視之，還需要在具體的實(shí)驗(yàn)中提煉出明確的焦點(diǎn)問(wèn)題。雙氣泡圖在進(jìn)入本次數(shù)學(xué)實(shí)驗(yàn)的過(guò)程中，以正方體表面涂色為基礎(chǔ)，通過(guò)比較、遷移，讓抽象、復(fù)雜的長(zhǎng)方體表面涂色的規(guī)律形成模型，清晰、直觀地呈現(xiàn)在學(xué)生眼前。雙氣泡圖的運(yùn)用，將兩個(gè)原本就緊密相連的對(duì)象在思維的層面再次激活，促使學(xué)生從兩個(gè)對(duì)象的相似與不同中受到啟發(fā)。

二、流程圖——在直觀中確立問(wèn)題引領(lǐng)，體驗(yàn)思維脈動(dòng)

數(shù)學(xué)實(shí)驗(yàn)也可以是由若干連續(xù)實(shí)驗(yàn)構(gòu)成的組塊實(shí)驗(yàn)，體現(xiàn)在后一次的實(shí)驗(yàn)都是對(duì)前認(rèn)知的深入，關(guān)注了對(duì)相關(guān)內(nèi)容的整體認(rèn)知與應(yīng)用。正因?yàn)檫@類(lèi)實(shí)驗(yàn)是由幾個(gè)實(shí)驗(yàn)串聯(lián)、并聯(lián)構(gòu)成，所以需要焦點(diǎn)問(wèn)題的溝聯(lián)。美國(guó)數(shù)學(xué)家哈爾莫斯指出，問(wèn)題是數(shù)學(xué)的心臟。問(wèn)題的設(shè)計(jì)對(duì)表象的思維訓(xùn)練及潛在的思維發(fā)展具有引領(lǐng)作用，教師要抓住某個(gè)最具價(jià)值的問(wèn)題，引領(lǐng)實(shí)驗(yàn)步驟，通過(guò)不同表征去層層推進(jìn)，而“流程圖”能夠結(jié)合不同的目標(biāo)情境，對(duì)某一程序性過(guò)程進(jìn)行恰當(dāng)?shù)牟襟E分解及有效歸并，引導(dǎo)學(xué)生在親歷探究中感受思維的脈動(dòng)。

例如，運(yùn)用流程圖可以預(yù)設(shè)分?jǐn)?shù)除以整數(shù)的學(xué)習(xí)路徑，再根據(jù)任務(wù)序列或者例題序列，賦予實(shí)驗(yàn)一定的邏輯遞進(jìn)關(guān)系，并在實(shí)踐中一步步優(yōu)化。

分?jǐn)?shù)除以整數(shù)的關(guān)鍵是對(duì)形如“4/5÷3”算理的理解，此時(shí)須讓學(xué)生明確三個(gè)意義：一是除法的意義，即平均分;二是分?jǐn)?shù)的意義，即把單位“1”平均分成若干份，表示這樣的一份或幾份的數(shù)用分?jǐn)?shù)表示;三是分?jǐn)?shù)乘法的意義，即求一個(gè)數(shù)的幾分之一用乘法。在實(shí)踐中，雖有三個(gè)意義保駕護(hù)航，但學(xué)生仍經(jīng)常出現(xiàn)用被除數(shù)的倒數(shù)與除數(shù)相乘的錯(cuò)例。顯然學(xué)生已具備抽象的概念理解，但沒(méi)能落實(shí)到直觀的表征運(yùn)用中來(lái)。

在充分認(rèn)識(shí)課本例題所蘊(yùn)含價(jià)值的基礎(chǔ)上，筆者結(jié)合原例題實(shí)驗(yàn)1又設(shè)計(jì)了三個(gè)實(shí)驗(yàn)，串聯(lián)起來(lái)分別是：1÷5（整數(shù)除以整數(shù)）→4/5÷2（被除數(shù)的分子能被整除的分?jǐn)?shù)除法）→1/5÷2，1/5÷3（單位分?jǐn)?shù)除以整數(shù)）→4/5÷3（被除數(shù)的分子不能被整除的分?jǐn)?shù)除法），將實(shí)驗(yàn)的焦點(diǎn)問(wèn)題直指實(shí)驗(yàn)4，并繪制了圖6。

沒(méi)有出示圖6前，學(xué)生獨(dú)立探究4/5÷2的計(jì)算，會(huì)“理所應(yīng)當(dāng)”地提出多種不同的計(jì)算方法，使得實(shí)驗(yàn)的方向轉(zhuǎn)為關(guān)注“算法的多元化”和“必要的優(yōu)化”這兩種關(guān)系的博弈，忘記了實(shí)驗(yàn)的目的是通過(guò)探究從而理解“除以一個(gè)不是0的整數(shù)等于乘這個(gè)數(shù)的倒數(shù)”。出示圖6后，學(xué)生可以清楚地發(fā)現(xiàn)，前三個(gè)實(shí)驗(yàn)是為解決實(shí)驗(yàn)4而設(shè)計(jì)的，這樣簡(jiǎn)單的方框和箭頭就能讓學(xué)生的思維從零散走向系統(tǒng)化。

實(shí)驗(yàn)1到實(shí)驗(yàn)4呈現(xiàn)組塊實(shí)驗(yàn)的特征，在此運(yùn)用流程圖，不僅是對(duì)步驟間的先后順序進(jìn)行審查，還能將碎片化的知識(shí)轉(zhuǎn)化為連貫性的想法，這種想法除了應(yīng)用還需理解，確保各實(shí)驗(yàn)環(huán)節(jié)的完整性。在這個(gè)意識(shí)的驅(qū)動(dòng)下，筆者引導(dǎo)學(xué)生在圖6的基礎(chǔ)上接著繪制。之后在組與組的圖示比照中，學(xué)生能意識(shí)到應(yīng)該在哪個(gè)實(shí)驗(yàn)環(huán)節(jié)重點(diǎn)表現(xiàn)關(guān)鍵因素（如圖7）。

圖7的出示，是學(xué)生在焦點(diǎn)問(wèn)題的引領(lǐng)下，運(yùn)用流程圖細(xì)化了分步目標(biāo)，再依據(jù)展開(kāi)的問(wèn)題進(jìn)行遞進(jìn)的實(shí)驗(yàn)探索。本圖示的生成，是學(xué)生在圖6已構(gòu)建出的算式模型的基礎(chǔ)上自主建立的數(shù)量關(guān)系模型，展示了學(xué)生對(duì)數(shù)學(xué)概念思想、結(jié)構(gòu)聯(lián)系之間的理解。數(shù)學(xué)思維的品質(zhì)最終在于抽象思維的高低，而抽象思維的水平是以表象的質(zhì)量和數(shù)量情況為轉(zhuǎn)移的，這次流程圖的出示也印證了莊惠芬老師指出的：從學(xué)會(huì)數(shù)學(xué)地思維走向通過(guò)數(shù)學(xué)學(xué)會(huì)思維。

三、樹(shù)形圖——在猜想中嘗試推理驗(yàn)證，呈現(xiàn)思維軌跡

由“形”的特征來(lái)勾畫(huà)出“數(shù)”與“式”，在聯(lián)通中發(fā)展學(xué)生的發(fā)散思維，從“點(diǎn)”到“網(wǎng)”，既而實(shí)現(xiàn)知識(shí)結(jié)構(gòu)的生成與重組，這種思維的建構(gòu)過(guò)程就如同一棵樹(shù)，主題是樹(shù)干，類(lèi)別是樹(shù)枝，類(lèi)別中的各個(gè)項(xiàng)目是樹(shù)葉，再由焦點(diǎn)問(wèn)題聯(lián)結(jié)成樹(shù)，最終形成直觀、有條理且不重復(fù)的樹(shù)形圖。樹(shù)形圖能夠?yàn)橐唤M實(shí)驗(yàn)提供多種合理的分類(lèi)方式，清晰地展示分類(lèi)間的相互聯(lián)系，而隨著思維的動(dòng)態(tài)進(jìn)程，最終形成涵蓋實(shí)驗(yàn)內(nèi)容的整合性圖示，這將成為后續(xù)思辨時(shí)的鮮活資源，其建構(gòu)過(guò)程亦可見(jiàn)學(xué)生的思維軌跡。

例如，運(yùn)用樹(shù)形圖可以有效厘清“釘子板上的多邊形”中，多邊形面積、邊上的釘子數(shù)和里面的釘子數(shù)三者之間的關(guān)系，從而助力學(xué)生在階梯式的猜想中迅速找到探究規(guī)律的切入點(diǎn)。

依據(jù)教材設(shè)計(jì)，本實(shí)驗(yàn)分三步。第一步，探索圍成的多邊形里只有1枚釘子時(shí)的規(guī)律、只有2枚釘子時(shí)的規(guī)律、只有3枚、4枚釘子或更多釘子時(shí)的規(guī)律。由于預(yù)設(shè)到釘子數(shù)與多邊形面積之間的關(guān)系相對(duì)復(fù)雜，故設(shè)計(jì)如圖8的研究單一，幫助學(xué)生進(jìn)行觀察、操作、比較，從而使學(xué)生明確：當(dāng)內(nèi)部的釘子數(shù)為l時(shí)，多邊形的面積等于邊上釘子數(shù)除以2。第二步，引導(dǎo)學(xué)生橫向觀察，得到多邊形的面積與邊上釘子數(shù)之間的關(guān)系，再啟發(fā)學(xué)生縱向思考：當(dāng)邊上的釘子數(shù)依次增加1枚時(shí)，面積如何變化。

這時(shí)，教師出示樹(shù)形圖（如圖9），并結(jié)合如圖10的研究單二，引導(dǎo)學(xué)生通過(guò)研究現(xiàn)有的里面釘子數(shù)為1、2、3-的多個(gè)實(shí)例，對(duì)初步得出的結(jié)論進(jìn)行驗(yàn)證。

鄭毓信教授指出：我們不應(yīng)將各個(gè)數(shù)學(xué)對(duì)象看成互不相關(guān)的獨(dú)立存在，恰恰相反，它們的性質(zhì)完全取決于它們的相互聯(lián)系。而數(shù)學(xué)本就是研究數(shù)量關(guān)系和空間形式的科學(xué)，樹(shù)形圖在此的運(yùn)用，是將看似獨(dú)立的點(diǎn)放置在系統(tǒng)中，從而使思維的軌跡可視。這個(gè)過(guò)程還可以幫助學(xué)生進(jìn)行類(lèi)比，找尋不同對(duì)象之間的聯(lián)系，使學(xué)生發(fā)現(xiàn)這類(lèi)對(duì)象的共同點(diǎn)。如圖9的出示，是在“固定其他因素，只讓某個(gè)量變化，從而得到問(wèn)題結(jié)果”這個(gè)策略指引下進(jìn)行實(shí)驗(yàn)的，當(dāng)里面的釘子數(shù)為1或2時(shí)，學(xué)生通過(guò)畫(huà)一畫(huà)、數(shù)一數(shù)、算一算等思維活動(dòng)驗(yàn)證關(guān)系式的正確與否，然后根據(jù)已有的兩個(gè)關(guān)系式之間的聯(lián)系，猜想當(dāng)里面釘子數(shù)是2、3、4……甚至是0時(shí)，又具有什么類(lèi)似的關(guān)系式。當(dāng)然，這些猜想并未經(jīng)過(guò)驗(yàn)證，同時(shí)預(yù)設(shè)的驗(yàn)證過(guò)程也并非一帆風(fēng)順，筆者認(rèn)為在后一階段的分工合作驗(yàn)證中，讓學(xué)生體驗(yàn)到小小的坎坷也是思維發(fā)展中應(yīng)該經(jīng)歷的。

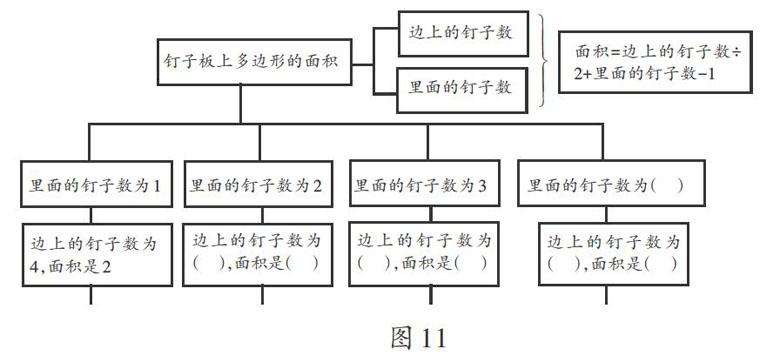
從抽象猜想到推理驗(yàn)證，整個(gè)思維軌跡在樹(shù)形圖的驅(qū)動(dòng)下逐步可視，當(dāng)學(xué)生看到圖9中由自己概括提煉出的相似結(jié)構(gòu)關(guān)系式時(shí)，自會(huì)生成此類(lèi)對(duì)象的“共通”關(guān)系式，最后筆者補(bǔ)充形成如圖11的樹(shù)形圖。這個(gè)思維結(jié)構(gòu)的建立過(guò)程也印證了鄭毓信教授的另一段話(huà)：我們由此獲得了一個(gè)既十分豐富又井然有序（或者說(shuō)，具有明確數(shù)學(xué)結(jié)構(gòu)）的“數(shù)學(xué)世界”。

圖示的運(yùn)用，為思維的延展提供了新的方式，筆者也在試著借此探尋學(xué)習(xí)的深處。基于對(duì)“數(shù)學(xué)實(shí)驗(yàn)的內(nèi)核就是學(xué)生思維培養(yǎng)”的理解，筆者將通過(guò)對(duì)此的研學(xué)，努力找尋數(shù)學(xué)知識(shí)與數(shù)學(xué)體驗(yàn)的思維結(jié)點(diǎn)。

[參考文獻(xiàn)]

[1]鄭毓信，小學(xué)數(shù)學(xué)教育的理論與實(shí)踐：小學(xué)數(shù)學(xué)教學(xué)180例[M].華東師范大學(xué)出版社，2017.

[2]潘小福，陳美華，小學(xué)數(shù)學(xué)實(shí)驗(yàn)教學(xué)的理論與實(shí)踐[Ml.江蘇鳳凰教育出版社，2018.

[3]潘香君，莊惠芬.構(gòu)圖，賦予學(xué)生創(chuàng)造性思維生長(zhǎng)的力量[J].江蘇教育，2015（09）.

[4]趙國(guó)慶，楊宣洋，熊雅雯.論思維可視化工具教學(xué)應(yīng)用的原則和著力點(diǎn)[J].電化教育研究，2019（09）.

（責(zé)編 李琪琦）