小學數學平面圖形面積思維導圖構建策略探究
唐海燕
(重慶市江津區石蟆小學校 重慶江津 402295)
思維導圖的運用就是要學生在學習的過程中聯系新舊知識,豐富學生已有的舊知識,將新的知識結構融進來,形成新的更寬廣的知識結構。這樣的教學方式有助于學生對知識進行歸納和理解,以便將數學知識更完整地展現在學生眼前。然而,一些教師仍采取傳統的教學模式,按照教材的內容對學生進行理論灌輸。本文主要針對小學數學平面四邊形面積思維導圖的構建策略進行探究。
一、小學數學應用思維導圖的意義
思維導圖主要是將知識點通過文字、圖形結合的方式逐級分層地呈現出來。這能幫助學習者快速進行學習和記憶。它能提升小學生的認知,幫助小學生學習數學知識,快速形成體系。這樣能有效避免小學生對數學感到枯燥無味,激起學生的興趣和共鳴,幫助學生不僅學會新知識,而且還培養其邏輯思維能力和抽象思考能力。因此,思維導圖這一行之有效的筆記方式和思維方式,在小學數學教學之中的應用是增強小學數學系統性和實效性的重要途徑,能實現學生發散思維能力和邏輯能力的提升,從而激發學生對學習數學的熱情。[1]
二、小學數學平面圖形面積思維導圖的構建策略
(一)結合思維導圖的特點,對圖形進行分類
學生年紀小,對一些講過的東西容易遺忘。數學教師如果想豐富學生的數學知識,就要讓學生學會分類歸納,對相關題型進行總結比對。通過思維導圖,學生能夠依靠一張圖紙,明確知道這一節課或這一題型在講什么,主要考究的知識點在哪里,從而在以后的做題過程中能夠穩準狠地找到解題關鍵。例如,教師在教授“平形四邊形”時,可以先提問學生,看看樹上的圖案是什么形狀?學生會看到編織圖案、籬笆和樓梯等。然后,教師再引出概念,這些由四條邊圍成的四邊形叫作平行四邊形。教師可讓學生拿出學具袋中的小棒,制作一個長方形框,再用手拉它一組相對的角,看這個框會變成什么形狀?反復做幾次,仔細觀察你能發現什么?這個圖形會發生變化,變得扁平或瘦高,不過他們還是四邊形。這些四邊形有統一的特點,有四條邊,且對邊相等,有四個角,卻都不是直角。學生才能知道歸類,并知道這些類似的長方形或者由長方形變形得來的圖形。這樣,學生思維上會有一個清晰的邏輯,記起來也更加容易,為以后學習平面圖形的面積打下堅實的基礎。[2]
(二)結合思維導圖的特點,優化數學解題結構
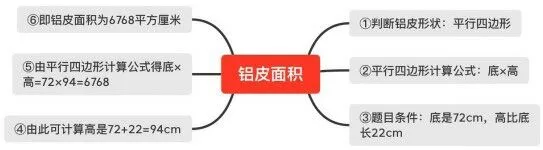
教師運用思維導圖對學生進行教育,可以將各個知識點關聯起來,其知識體系將會變得更加清晰。這樣能培養學生的自主探究能力。教師要根據實際情況對學生展開指導,促進學生學習能力的提高。然而,涉及的知識點過多會不利于學生理解和記憶。教師可通過思維導圖對知識進行總結,讓學生對知識之間的關聯性進行有效總結,優化學生的認知結構。例如,在計算“平行四邊形”的面積時,教師可先讓學生試一試,如一塊平行四邊形的鋁皮,底是72cm,高比底長22cm,求這塊鋁皮的面積。小學生就會開始思考,要求平行四邊形的面積,就要知道底和高。學生理解了這個概念后,教師就可讓其進行實際運算,在實踐中鞏固練習。例如,底是18米高是8米的平行四邊形的面積是多少?學生就會計算18×10,從而得出平行四邊形的面積為180平方米。然后,教師可以用PPT給同學展示一些四邊形的圖片,讓其口算。這樣通過反復練習,學生就會掌握一種規律,即四邊形的面積一般都是“底×高”。這樣,從認識圖形到圖形面積的計算,整個思維是流暢的,學生在邏輯思維的引導下,其記憶力會變得超好。
(三)結合思維導圖的特點,突破課堂教學難點
在小學數學課堂中最難的就是重難點知識的講解。教師雖然花費了很多時間和精力,但學生就是不懂。因此,小學數學教師應該通過思維導圖把相關的抽象知識具體形象地展示在學生面前,從而促進學生更好地學習,提高小學數學課堂的效率。例如,在學習“三角形面積”的計算時,教師可以先讓學生拿出兩個一樣的三角形拼一拼,看其能拼出什么圖形?學生會發現長方形是由兩個一樣的三角形組成的。既然長方形的面積計算公式是“長×寬”,那么三角形的面積自然就是長方形面積的一半。這樣,三角形的面積就很容易推導出是“長×寬÷2”。這樣的思維培養增強了學生的數學推理能力。[3]
三、結束語
綜上所述,隨著新課改的深入,思維導圖教學法有效調動了學生的學習積極性,優化了其自身的思維結構,培養了學生的數學思維。教師通過結合教材內容,對平行四邊形面積進行分類總結,幫助學生記憶,使其對零散知識進行系統化、結構化整理,幫助學生形成了關于平面圖形面積的思維網絡,提高了其記憶力和理解力。同時,這也構建了高效的數學課堂模式,給廣大數學教育從業者提供了諸多參考。

