數學思想方法在《離散數學》教學中的應用研究

李艷艷

(文山學院數學學院 云南文山 663099)

數學思想方法主要包括化歸思想方法、類比思想方法、逆向思維思想方法、數形結合思想方法、分類思想方法、抽象思想方法、變換思想方法七類。本文研究在“離散數學”課程教學中，如何有效地貫穿和應用數學思想方法。知識的學習是暫時的，而掌握了思想方法才是永恒的。

一、化歸思想方法及應用

二、類比思想方法及應用

類比思想方法指的是通過兩個研究事物的比較，推斷出它們相同或相似的特征。

三、逆向思維思想方法及應用

四、數形結合思想方法及應用

數形結合思想就是通過數和形之間的對應關系和相互轉化來解決問題的思想方法。

集合部分的學習技巧之一就是采用數形結合。主要采用文氏圖表示集合的基本運算和有限集的計數問題。

二元關系的關系圖和有窮集的偏序集的哈斯圖都是結合了數形結合的思想。

五、抽象思想方法及應用

抽象思想方法主要在解決一些復雜的實際應用案例時，需要將條件抽象成數學問題，然后用數學的手段解決。

例如：如果張三作案，那么李四一定是主犯；如果張三沒作案，那么王五參與作案。如果李四不是主犯，那么王五沒有參與作案。

由此可以推出以下哪項？（）

A.張三沒作案

B.李四一定是主犯

C.李四不一定是主犯

D.王五參與作案

E.張三作案

命題符號化：設p：張三作案，：q李四為主犯，r：王五參與作案，

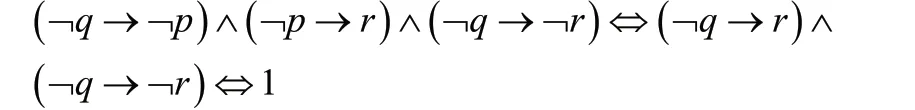
從而推斷李四是主犯的結論。

六、結束語

數學學習的靈魂是思想方法，不是知識本身。本文通過列舉五類數學思想方法在“離散數學”課程教學中的具體應用，將數學思想方法進一步很好的詮釋。也使學生們進一步深刻體會不同數學課程背后的共同點就是數學思想方法。