基于“構造法”的高中數學解題思路探索

顧建華

(云南省昭通市大關縣第一中學 云南昭通 657400)

構造法就是根據數學問題條件或者結論的特征，以問題中的數學元素為“元件”，數學關系為“框架”構造出新的數學對象或者數學模型。將抽象的問題具象化，使學生快速理解題目，從而有效提高學生的數學解題能力和課堂效率。

一、構造法在函數解題中的運用

在面對“導函數”這一必學知識點時，運用構造法，幫助學生根據現有的條件使用構造法對函數進行解答，并且找出函數的性質，接著運用圖形加以論證結果的正確性。因此，在解決這類問題的過程中，運用構造函數的方法可以幫助化繁為簡，而且依靠構造法本身的靈活性和技巧性幫助學生更加直白地明白題目的含義。

如已知函數f(x)=axlnx+b(a，b為實數)的圖像在點(1，f(1))處的切線方程為y=x-1。

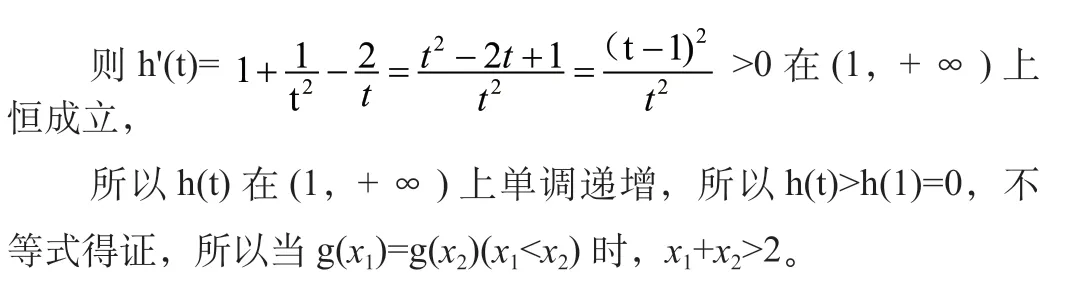
二、構造法在解數列中的運用

在高中階段，求數列是高考考查的重點和熱點，比如在等比數列中的運用方式，運用乘、除去分母、添項、去項、待定系數等方法，將遞推公式變形為f（n+1）=Af（n）(其中A 為非零常數）形式，根據等比數列的定義知f（n）是等比數列，根據等比數列的通項公式，先求出f(n)的通項公式，再根據f（n）與an，從而求出an的通項公式。

分析：本題是兩次構造等比數列，屬于構造方面比較級，最終用加減消元的方法確定數列的通項公式。

三、構造法在圖形解題中的運用

高中數學知識學習過程中，數形結合是非常重要的數學思想，被大量使用在各種類型的數學題目當中，學生通過圖形構造法可以幫助認識到問題的關鍵所在，例如運用構造直角三角形來解決函數中的一些常出現的問題。直角三角形有其直角的特點常常被用在解決數學問題中，幫助學生將抽象的問題變的具象化[1-2]。

四、結束語

綜上所述，教師應該引導學生熟練掌握構造法并且會靈活運用在各種題型當中，幫助學生從多角度去考慮解題思路，上述例子都在說明在面對按照定向，按照常規難以解決的情況下做出改變，開拓更多的數學解題思維，降低題目的難度，使抽象的數學題目變得更加直觀具象，單一型轉變為多角度，有效提高數學解題的效率。