高職數學教學中融入教育元素的實踐與研究
——以極限概念教學為例
王詠芳
(蘇州健雄職業技術學院,江蘇 太倉 215411)
1 極限概念的引入
引例1:莊子(前369年—前286年,戰國)曾寫道:“一尺之棰,日取其半,萬世不竭。”當n越來越大時,棰越來越短,逐漸趨于0,這里從直觀上體現了極限思想。
引例2:劉徽(約公元225-295年,魏晉時代人)創造了用“割圓術”來計算圓周率的方法,從而開創了我國數學發展中圓周率研究的新紀元。他從圓內接正六邊形算起,依次將邊數加倍,以致算到內接正3 072邊形的面積,從而得到圓周率π的近似值3.1416,后人為了紀念劉徽,稱這個數值為“徽率”。這里他已經把極限的思想應用于近似計算,這種方法比歐洲早了1 000多年。
利用兩個引例,以數學文化為背景,借助科學家們的真實事跡,引導學生要善于觀察,善于思考,善于總結。
2 極限概念的分析與解讀
2.1 數列極限
數列極限的(描述性)定義:在數列{xn}中,如果當n無限增大時,xn無限地接近于確定的常數a,則稱當n趨向于無窮大時,數列{xn}的極限為a,也叫做數列收斂于a;否則就稱數列是發散的。
解讀1 “n無限增大”:就是要求數列必須是無窮數列,也就是說極限問題中的數列必須是無窮數列。
解讀2 “確定的常數a”:是指唯一的常數,而后面的“否則”是指a的不唯一或不確定。
解讀3 數列的極限只有收斂或發散,二者只居其一也必居其一。發散的數列也可以叫做不收斂的、沒有極限的,還可以叫做數列極限不存在。
解讀4 “無限地接近于”、“趨向(于)”:這是兩個相同意義的文字描述,也是描述性定義的缺陷和不精準所在。用下面兩個收斂數列解說:
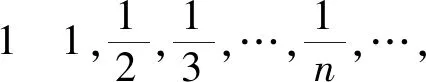


解讀5 既然是總體的變化趨勢,那么數列的前有限項的變化:變項值、去除、添加等,對數列的極限不產生影響,即可以有下面的定理:
定理 數列中去除、添加有限項后的新數列,其斂散性不變。
試想一下:{xn}與{kxn}(k≠0)的斂散性有變化嗎?
解讀6 數列的無窮多項的變化,將導致斂散性發生變化。
數列3a,a,a,…;
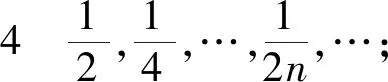
當a=0時,數列3和數列4是數列2的兩個子數列,分別為奇數項子數列和偶數項子數列,也可以說是數列2去除無窮多項后的數列,因為數列2是收斂的,所以數列3和數列4都是收斂的。
當a=2時,數列3和數列4仍都是收斂的,若仍分別為奇數項子數列和偶數項子數列,則原數列是發散的。
2.2 函數極限
2.2.1 當x→∞時的情形
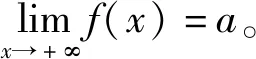
類似地,可定義函數f(x)在x→-∞時或在x→∞時的極限。
解讀1 在描述性定義中,自變量趨于無窮(x→∞)時的函數極限與數列極限是相似的,主要區別是:函數中自變量可以不是正整數,是實數范圍;自變量的變化不要求單調的。
解讀2 記號“x→∞”稱為“x趨向于無窮(大)”,而實際上它細分為3種情形:x取正值無限增大,記作x→+∞,稱為“趨向于正無窮”;x取負值而無限增大,記作x→-∞,稱為“趨向于負無窮”;x可取正值也可取負值,而|x|無限增大,記作x→∞,稱為“趨向于無窮”。
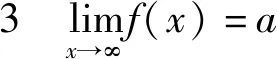
2.2.2 當x→x0時的情形
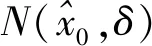
解讀1 自變量趨向于有限數(x→x0)是指自變量x并不要求等于(取到)x0,即:函數值f(x0)的有無或大小并不影響極限存在與否。
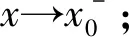
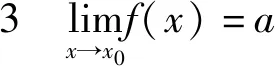
3 極限符號的書寫
總之,極限的概念是有眾多可以推敲的地方,是體現數學思想的場所,是引導學生學會發現問題、分析問題、解決問題的練兵場。在教學過程中恰到好處地融入一些教育元素,使學科教育與思政教育做到和諧統一,更好地實現既教書又育人。

