培養學生發散思維能力的課堂實踐研究探索

劉麗

【摘要】創新是國家發展的核心動力，培養創新人才是國家教育的核心使命，創造性思維是培養創新人才的關鍵。正如楊振寧博士指出：中國的學生知識豐富，善于思考，但卻不善于想象、發揮和創造。因此，培養學生的創造性思維至關重要。發散思維能力是創造性思維的重要組成部分，在初中數學教學中，培養學生的發散思維，能夠擴展學生的解題思路，擴大學生思維的開闊性，有利于學生養成良好思維習慣，有利于學生創新能力的形成。

【關鍵字】初中數學? ?發散思維能力? ?課堂實踐

【中圖分類號】G633.6【文獻標識碼】A【文章編號】1992-7711（2020）08-028-02

創造性思維是以新穎獨特方法解決問題的思維過程，它是人類思維的高級過程，是人類意識高度發展的標志。發散思維是創造性思維的核心要素，培養學生發散思維能力是數學教學的重要任務。優化數學教學策略，強化學生理解能力，提升學生思維品質，強化學生思維靈活性，鍛煉學生思維敏捷性，把拓展學生發散思維滲透到教學各個環節，培養學生從不同角度、不同層次發現問題和思考問題的能力。發散性思維屬于求異思維，這種思維的特點是注重從不同方面，不同角度和不同側面尋找問題的解決答案，對問題信息由可能的地方向延伸拓展擴散，進行放射性聯想和邏輯推理。能夠熟練使用發散思維思考問題，往往是一個人思維的靈活性、敏捷性和深刻性的標志。發散思維能夠擺脫思維的定式，是發現新知識的重要思維方式。

一、在課堂教學中進行“課堂提問”教學藝術研究

良好的課堂提問是教學成功的關鍵，它能激發學生動力，集中學生注意力，促使學生思考，訓練學生思維，培養學生問題意識，讓教師更好掌握學生學習情況。當前數學老師的課堂提問依然存在許多問題，主要有：課堂提問內容局限于教材;提問數量相差大;識記性問題和管理性問題比例較高，基本沒有發散性問題;課堂提問參與率不高，幾乎沒有學生主動提出問題。

（一）設計“問題串”，引發學生追問。教師針對課堂內容，尋找“有意義的切入點”，針對切入點設計一個個的“問題串”，使學生通過回答一個個問題，加深對知識的理解，培養學生數學思維。教師通過合理追問，充分發揮課堂追問效能，對課堂重難點進行有效突破，提高學生參與度，激發學生散發思維，以問促思，以問促問，形成具有邏輯的“問題串”，有效落實教學效果。

（二）“高認知提問”，引發學生思考。教師針對所學內容進行的理解性提問和評價性提問，需要學生進行一系列的思考、歸納、總結，才能做出創造性的回答，這屬于“高認知提問”。普通的課堂提問往往局限于識記性提問、管理性提問和提示性提問，對學生思考沒有充分的關注，降低了提問的認知要求，導致學生課堂思維層次低下。高認知提問能夠使教師靈活運用提問藝術，激發學生學習興趣，促進學生高層次思維，促進課堂活動的高效性和流暢性。

（三）善用發散性提問，提升學生思維層次。發散性提問激發一般的開放性的回應，沒有唯一的答案，任何答案都有可能是正確的。發散性提問重要功能是，能夠激發學生多角度觀察事物，能夠細致思考問題，能夠促使學生用最優手段進行全面思考歸納，探索和解決問題，對于培養學生創新思維、逆向思維、求異思維、發散思維等方面發揮關鍵作用。教師設計發散性提問時，應該考慮學生對知識的掌握程度，以及應用知識的熟練程度，通過例題或習題，設計出發散性提問，做到一問一思，一問多思，鼓勵學生運用創造性方法解決問題。

二、激發學生“聯想猜想”，培養學生的發散思維能力

數學課程設計的過程，一般是先有猜想，然后對猜想進行驗證和應用的過程。我們知道，猜想是以聯想為中介，在新課程標準下，猜想和聯想的數學思維方法，是數學教學中常用的方法，教師要經常運用猜想和聯想方法，不斷改變教學模式和方式，加強對學生對猜想和聯想數學思維的方法指導。聯想是形成發散思維的重要環節，有助于指導學生從不同方面進行思考問題。對于有些探索性問題，因為沒有明確的條件和結論，就需要鼓勵和引導學生，去發現題中的隱含條件，并做出合理地猜想和論證。

三、逆向應用公式和法則，發展學生逆向思維能力

逆向思維也叫求異思維，是對司空見慣的定論事物或觀點進行反向思考的一種思維方式，即通常所說的“反其道而思之”，從問題的反面進行探索，樹立新思想，創立新形象。逆向思維和發散思維都是創新思維的重要方式，在八年級整式乘法的教學過程中，學生熟悉了整式乘法的法則和乘法公式后，可以熟練的正向應用公式法則，還要在此基礎上進行適當的逆向練習，培養學生的逆向思維能力，培養學生逆向應用公式和法則的能力。

四、在課堂教學中進行“變式教學”研究

采用不同的思維能力，就決定著不同的課堂教學形式。例題習題教學是數學教學的重要組成部分，是聯系數學知識、技能、思想和方法的紐帶，采用例題習題教學方式，可以強化知識基礎，傳授教學方法，揭示數學規律，啟迪數學思維，激勵教學創新，培養思維能力。在日常的數學教學中，容易形成思維定勢，套用解題模式，造成思維呆板僵化。因此，在數學例題習題教學中，在學生掌握基本方法后，應當通過改變題型、條件、結論、方法、情境等多種途徑，強化學生對知識的理解，對方法的變通，學會多角度、多層次、多方向的分析和思考，突破固定思維模式，提出新的問題及新的解決方法。例如，以例題習題變式的一題多變變式為例。一題多變變式，就是通過對某一題目進行條件多變、結論探索、逆向思維、圖形多變等多角度多方位探索，使一個題變化為一類題，達到舉一反三、觸類旁通的目的，培養學生良好的發散思維能力。一題多變變式主要包括條件變式、結論變式、逆向變式、圖形變化等四種變式。

1.條件變式：對某一題目的某一條件進行變化，保持結論不變。

①如圖1，已知，△ABC是等邊三角形，BD 平分∠ABC延長BC到E，使CE=CD，連接DE，試判斷BD與DE的大小關系，并說明理由。

②變式1：把條件“BD平分∠ABC”改成其他什么條件，還能得到同樣的結論？

③變式2：當點D是AC邊上任意一點，且CE等于AD，上述結論還成立嗎？

引導學生通過對題目條件變式并給予解答，培養學生提出問題、分析問題和解決問題的能力。

2.結論變式：某一題目條件不變，將問題的結論進行拓展，使一般性習題轉化為開放習題。

如圖2，點A，B，C在同一條直線上，△ABD，△BCE均為等邊三角形，連結AE和CD， AE分別交CD，BD于點M，P，CD交BE于點Q，連結PQ，BM.

求證：①△ABE≌△DBC;②∠DMA=60°;③△BPQ為等邊三角形。

結論變式由相同的條件為出發點得出多個的推理結論。學生的思維視野廣闊，呈現出多維度發散狀態，培養和提高了學生的發散思維能力。

3.逆向變式：引導學生分析、探究所解命題的逆命題是否成立，培養學生逆向思維能力。

如圖3，已知：在△ABC中，AD平分∠BAC，∠C=2∠B，求證：AB=AC+CD.

變式：已知：AB=AC+CD. 求證：在△ABC中，AD平分∠BAC，∠C=2∠B。

通過逆向變式，訓練學生的逆向思維，引導學生以此來判斷原命題的逆命題是否為真命題。對學生思維能力的培養有很大提高。

4.圖形變式：是以原圖形為生長點，通過對原圖形平移、翻折、旋轉等變換，從而得到新的變式題組。

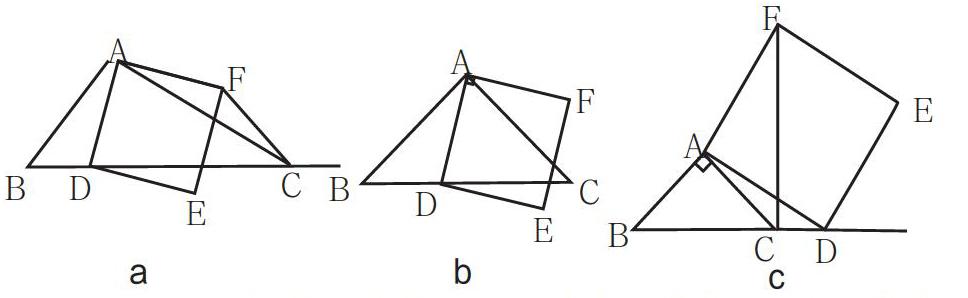
如圖a，在△ABC中，∠ACB為銳角，點D為射線BC上一點，連接AD，以AD為一邊且在AD的右側作正方形ADEF.

（1）如果AB=AC，∠BAC=90°，

①當點D在線段BC上時（與點B不重合），如圖b，線段CF，BD所在直線的位置關系為? ? ? ? ? ? ? ?，線段CF，BD的數量關系為? ? ? ? ? ? ? ? ? ?;

②當點D在線段BC的延長線上時，如圖c，①中的結論是否仍然成立，并說明理由;

（2）如果AB≠AC，∠BAC是銳角，點D在線段BC上，當∠ACB滿足什么條件時，CF⊥BC（點C，F不重合），并說明理由.

圖形變式以動態的形式展示圖形結構的變化，既培訓學生的觀察能力，空間想象能力又在推理求證的過程中培養學生的邏輯推理能力。

總之，數學例題習題的變式不是為了變式而變式，而是要根據數學教學要求，遵循學生對數學的認知規律而設計的數學變式。通過數學變式訓練，能使學生在有限時間內，將學到的數學知識轉化為解題能力，形成數學解題技能，拓展數學發散性思維，提升數學思維創新能力。

【課題項目：本文系河南省教育科學規劃一般課題《初中數學課堂中培養學生數學思維能力策略研究》（編號：〔2019〕-JKGHYB-1229）研究成果。】

[參 考 文 獻]

[1] 陳佳蘭.初中數學教學中培養學生發散思維有效策略的實踐研究[D].上海：上海師范大學.2019.

[2] 沈吉文.數學課堂培養學生高階思維能力實踐研究[J].成才之路.2019（08）：36

[3] 范叔旺提高課堂例題有效設計，培養學生發散思維能力[J].數學學習與研究.2018（23）： 126-127.