培養(yǎng)學生思維能力的幾點“題”議

彭先才

(重慶市秀山縣教師進修學校 重慶 409900)

義務教育數(shù)學課程標準提出，培養(yǎng)學生的思維能力和創(chuàng)新意識是現(xiàn)代數(shù)學教育的基本任務。數(shù)學教師應把培養(yǎng)學生的思維能力，發(fā)展學生的核心素養(yǎng)貫穿于教學的全過程。筆者結合教學實踐，以題為例談談培養(yǎng)學生思維能力的幾點嘗試。

一、一題多解，培養(yǎng)思維的發(fā)散性

一題多解是指對于一道習題，能從多個不同角度去思考問題、分析問題，從問題的不同角度尋找到不同的解題方法，并對這些不同解題方法進行總結和歸納，此方式能培養(yǎng)學生思維的發(fā)散性。在課堂上，適時地交流多種解題思路，可以加深學生對所學知識的理解，訓練學生對數(shù)學思想和數(shù)學方法的嫻熟運用，激發(fā)學生主動發(fā)現(xiàn)和創(chuàng)造的強烈欲望，促進學生思維的發(fā)散，培養(yǎng)學生的創(chuàng)新思維。

例如：修路隊要修一條長480米的公路，5天修了160米，照這樣計算，余下的公路需要幾天修完？

方法1：先求出一共需要的天數(shù)，再求還要幾天修完。

解法一：480÷(160÷50)-5

解法二：5÷160×480-5

解法三：5×(480÷160)-5

用不同的方法先求出總天數(shù)，加深學生對數(shù)量關系和數(shù)學概念的理解和運用。

方法2：先求出余下公路的長，再求還要幾天修完。

解法四：(480-160)÷(160÷5)

解法五：(480-160)×(5÷160)

解法六：5×[(480-160)÷160]

方法3：用倍比方法解答。

解法七：5×(480÷160-1)

以上教學過程，學生的解法多樣，表明學生的思維靈活，思路開闊。再通過對比小結，相互啟發(fā)，優(yōu)化方法，達到對知識的融會貫通，一題多解能充分發(fā)掘?qū)W生自身的潛能，使其養(yǎng)成從不同角度觀察和思考的習慣，從題目的各個方面對問題進行分析、解答，進而提高學生解題的邏輯思維能力。

二、一題多變，培養(yǎng)思維的深刻性

一題多變是指從多角度、多方位對例題進行針對性變化，生成多道相近、相似的實際問題，體現(xiàn)知識的規(guī)律性和關聯(lián)性，讓學生更加熟練地掌握應用的數(shù)量關系和解題方法，培養(yǎng)學生靈活解題的能力，同時訓練學生思維的靈活性和深刻性。

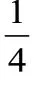
通過一題多變，一道實際問題經(jīng)過兩次變式，每一次變式都體現(xiàn)了知識間的內(nèi)在聯(lián)系，教師引導學生說出解題思路，尋找題目中的對應關系，用類比的方法思考和學習，使學生理解分數(shù)實際問題中的數(shù)量關系，從而提高學生綜合應用分數(shù)知識解決實際問題的能力。

三、一題多問，培養(yǎng)思維的靈活性

一題多問，是根據(jù)已知條件與所求問題之間的關系，提出多個不同問題，使學生靈活運用所學知識解決問題。問題意識是創(chuàng)造性、創(chuàng)新能力的基礎，創(chuàng)造始于問題。如：一項工程，由一個隊獨做，甲要10天，乙要15天，丙要12天。①三隊合作需要多少天？②甲隊先做4天，剩下的三隊合做，還需多少天？③三隊合做2天，剩下的由丙隊獨做，還需多少天？④先甲乙兩隊合做3天，剩下的由乙丙兩隊合做，還需多少天？

一題多問能使學生對題中的數(shù)量關系隨機應變，舉一反三，觸類旁通，能培養(yǎng)和鍛煉學生發(fā)現(xiàn)問題、提出問題、解決問題的能力，進而提高學生的創(chuàng)造性思維。

四、多題一解，培養(yǎng)思維的變通性

同一種數(shù)學思想方法解決不同的數(shù)學問題我們稱之為“多題一解”。在解題過程中，為強化某一解題方法，我們可將一些不同內(nèi)容的練習題批編在一起，讓學生用同一種方法去解，達到強化訓練的目的，提高學生解題技巧技能，收到舉一反三、觸類旁通的效果。

多題一解，能夠加深學生的思維深度，分析事物時學會由表及里，抓住事物的本質(zhì)，找出事物間內(nèi)在的聯(lián)系，把握事物的共同點，構建數(shù)學模型。

總之，在數(shù)學教學中要提高學生的數(shù)學思維能力。實踐證明，設計好例題，運用好例題是培養(yǎng)學生思維能力的有效方法，不僅能提高學生的學習效率，而且對學生核心素養(yǎng)的發(fā)展有十分關鍵的影響，當然，教學時要注意幾種方式相互結合，靈活運用，不可只求一技，失之偏頗。