平行公理的尺規作圖方法聚焦
蔣雪梅
(重慶市永川區朱沱鎮四明初級中學校 重慶 402160)
尺規作圖指用無刻度的直尺和圓規作圖,起源于古希臘的數學課題。只使用圓規和直尺,并且只準許使用有限次,來解決不同的平面幾何作圖題。在人教版七年級下冊第五章相交線與平行線第二節中,得到了一個基本事實,即平行公理:經過直線外一點,有且只有一條直線與這條直線平行。可是教材中已把這部分的尺規作圖簡化了,部分教師是用三步法畫平行線,一放,二移,三畫。但這個平行公理的尺規作圖又該怎么畫呢?有沒有巧妙的方法呢?下面作者聚焦了幾種以幾何原型為參照的平行公理的尺規作圖方法。
問題:已知直線l與直線外一點A,過點A作與直線l平行的直線。(要求:尺規作圖)
對于用尺規作圖來畫出平行公理中平行線的問題,從平行線判定的角度考慮,得到如下幾種尺規作圖原型。
一、平行線的判定原型
(一)同位角相等,兩直線平行
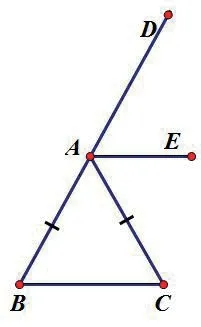
幾何原型1
畫法:1.在直線l上任取一點B,以點A為圓心,以AB長為半徑畫弧,交直線l于點C(不與B點重合);
2.構造等腰三角形ABC;
3.作等腰三角形ABC頂角的外角∠CAD的角平分線AE,則直線AE即為所求。
證明:∵AB=AC
∴∠B=∠C
又∵∠DAC是∠BAC的一個外角,AE平分∠DAC
∴∠DAE=∠B
∴AE∥BC
(二)內錯角相等,兩直線平行
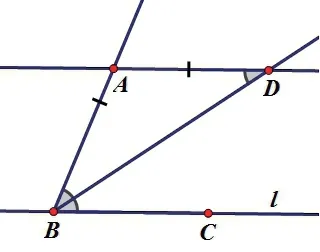
幾何原型2
畫法:1.在直線l上任取兩點B.C;
2.作∠ABC的角平分線BD;
3.以點A為圓心,AB為半徑畫圓,交射線BD于點D;
4.連接AD,直線AD即為所求。
證明:由圖可知:AB=AD
∴∠ABD=∠ADB
又∵BD平分∠ABD
∴∠ABD=∠DBC
∴∠ADB=∠DBC
∴BC∥AD
二、平行四邊形原型
(一)兩組對邊分別相等的四邊形是平行四邊形
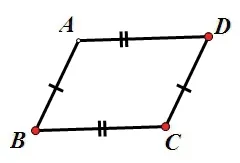
幾何原型3
畫法:1.在直線l上任取兩點B,C;
2.分別以A、C為圓心,BC、AB為半徑畫弧,兩弧交于點D;
3.連接AD構造平行四邊形ABCD,則直線AD即為所求。證明略。
(二)對角線互相平分的四邊形是平行四邊形
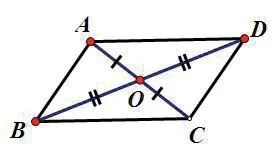
幾何原型4
畫法:1.在直線l上任取兩點B,C;
2.連接AC;
3.作AC的中點O;
4.連接BO并延長至點D,使得BO=DO;
5.連接AD,則直線AD即為所求。
證明略。
三、三角形的中位線原型
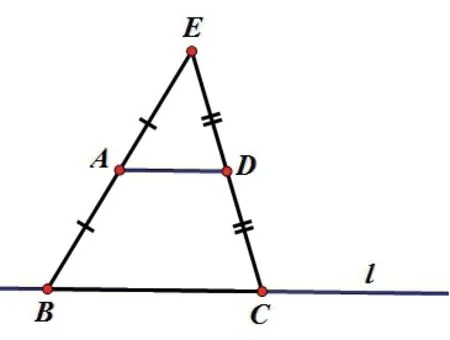
幾何原型5
畫法:1.在直線l上任取一點B,連接AB并延長至點E,使得AB=AE;
2.在直線l上再取一點C(不與B點重合),連接EC;
3.作線段EC的中點D;
4.作直線AD,則直線AD即為所求。
證明略。
四、結束語
通過參照幾何原型對平行公理進行尺規作圖,不僅給了學生尺規作圖的思考方向,而且能提高學生思考問題的能力和動手能力,多角度思考問題的能力,體現了新課標下的以學生為主體,老師為主導的思想,能使不同層次的學生得到不同的發展。

