《數學分析原理》中的方法探索與應用
(首都師范大學 北京 100048)
1 分析簡介
本書由實數和復數的簡單討論開始 (第一章),但這一章的最大亮點是在它的附錄里:戴德金分割。它告訴你如何通過有理數來構造無理數。第二章是基本的拓撲知識,這些都是后面要用的。所以它們看似簡單,但不能忽略。第三章中的數列和極限也是后面要用到的基本知識,這些對於中國的學生也許是不太難的。作者把極限的正式引入推遲到數列的收斂之后 (第四章)顯然符合循序漸進的原則,也是國內大多數教材的思路。積分部分 (第六章)關于黎曼-斯蒂爾吉斯積分的一章是作者在第三版花了較大工夫的部分。這是在初等微積分的基礎上對(實值、復值和向量值)積分概念的嚴格化。注意有些定理是基于黎曼積分進行討論的。函數序列與函數項級數(第七章)是第三章中數列與級數的討論的延伸。這可以說是本書最重要的部分了。本章要解決的是兩個極限交換的問題,魏爾斯特拉斯一致逼近定理起了關鍵作用。有了第七章的準備,作者在下面的一章里討論了一些特殊函數。第九章轉到多元函數。本章里的線性算子就是泛函分析中的更為抽象的 Banach空間中的重要概念。第十章是微分幾何導引。主要是Stokes定理。這里我主要想分享一些由書中知識點得到的一些聯想和啟發。
2 恒等式產生不等式的應用

于是定理保證
y=supE


但y-k<y,這與y是E的最小上界的事實矛盾。
應用延伸:下述極限存在且有限:

式中,e≈2.7182818稱為自然底數。
證:令 b>a>0,有
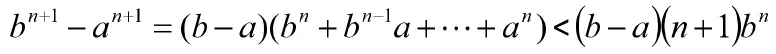
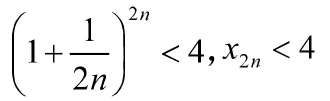
3 積分的引入
這個思路是幾何學中的經典與精華:證明球的表面積和它半徑與高度都相同的圓柱的表面積,嚴格來說,是沒有上下兩個面的圓柱。把圓柱展開成長方形,長方形的寬是圓柱底面的周長2 R,長方形的高是球的高度,也就是2R,不難發現,長方形面積即球面積表達式4 R2。問題是,球面怎么與柱面聯系起來。基本思路是用許多覆蓋球面的小長方形來估計表面積,然后再將這些小長方形直接向外投影,看看它們是什么樣,就像是由放置在z軸上的小燈,朝著與xy平面平行的方向照出陰影一樣。而令人驚訝的是,小長方形在圓柱面上的投影面積正好等于原始小長方形的面積。其實,這里有一個此消彼長的效應。我們把沿著緯線的邊叫寬,沿著經線的邊叫高。一方面,我們把小長方形向外投影時,它的寬會被放大。對于靠近兩級的小長方形來說,這個長度被放大得很厲害,因為投影的距離相當長,而對于靠近赤道的小長方形來說投影幾乎沒有什么影響,但從另一方面來說,由于這些小長方形和z方向有一定角度,在投影過程中,小長方形的高會被縮小,在這種思路下,靠近極點的小長方形傾斜得很厲害,所以它們的高也會被擠壓得很厲害,而靠近赤道的小長方形基本上和z軸平行,就不會被擠壓太多。最終,這兩種互相競爭的效果,也就是寬度上的拉伸和高度上的擠壓完美地抵消了。當然,關鍵在于說明為什么兩種競爭效果可以抵消。


大體思路是把球面切成許多和xy平面平行的細環,然后對比這些環的面積和環在 xy平面上投影的面積。找到這些環的陰影和球面上偶數號的環之間的對應關系。用 表示環到球心連線和z軸的角度,把相鄰環之間的角度差叫做d,也就是說,每個環的厚度是半徑R乘d,這個環的內側周長是2 Rsin,乘以厚度Rd,就是這個環的近似面積,當你把球面切得越來越細時,這個近似值也越來越準確。而其中一個環在xy平面上的陰影面積是2 Rsin cos d,而每一個環的陰影面積恰好等于球面上每一個環原始面積的一半,這里說的環不是陰影正上方的環,而是距離夾角為2的環(sin2=2sin cos)。即一個半球的表面積是兩個同半徑圓的面積,故一個球的表面積為四個相同半徑圓的面積。
由此我們引入積分的公式及含義,這是讀這本書時我所想補充的。
4 偉大的數學家Cantor
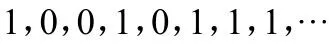
這就證明了A的每個可數子集是A的真子集。因此A是不可數集(否則A將是它自己的一個真子集,這不可能)。
以上證法的思想是Cantor首先使用的,并且稱為Cantor的對角線手法。
叫做Cantor集。P顯然是緊的,而且P不是空集。
如果k和m都是正整數,那么沒有一個形式為

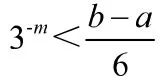
所以P不能含開區間。
Cantor集的一個非常有趣的性質是,它給我們提供了一個測度為0的不可數集的例子。
5 Lebesgue測度的建立
測度空間:假設X是一個集,它不必是歐式空間甚至任何度量空間的子集。如果存在X的子集(稱它們為可測集)組成的—環,及定義在上的一個非負可數可加集函數稱為測度),就說X是測度空間。
由我們所學概率論可以提出一個例子,事件可以看成是集,而事件發生的概率是可加(或可數可加)集函數。

