土釘加固小窯采空區穩定性評價的隨機抽樣法

李濤 劉泓霖 張波

摘 要：為了評價土釘加固的小窯采空區的穩定性，探討了基于土釘加固的太沙基土拱理論的隨機抽樣法。統計小窯采空區穩定性因素的參數和概率分布，循環生成各因素的隨機數并應用土釘加固的太沙基土拱理論判斷穩定性，最后用失效頻率估計失效概率。結果顯示，基于土釘加固的太沙基土拱理論的隨機抽樣法計算得到的失效概率和隨機有限元法仿真得到的失效概率差別不大。小窯采空區的目標失效概率與上部結構的安全等級和地基的破壞類型有關。通過隨機抽樣法獲得的斜土釘加固小窯采空區的穩定性評價結果，比強度折減法更有說服力。

關鍵詞：小窯采空區;斜土釘加固法;太沙基土拱理論;隨機抽樣法;隨機有限元法

中圖分類號：U45+.2 文獻標識碼：A 文章編號： 1671-2064（2020）12-0165-04

0引言

小窯采空區范圍窄，開采淺，以巷道和支巷道采掘為主，呈網格狀或無規律分布，單層或多層重疊交錯，大多不支撐或臨時簡單支撐，其地表易產生較大的裂縫、臺階和陷坑，嚴重威脅上部已建或擬建的建構筑物的安全[1]。

為保證小窯采空區上部結構的安全，提出斜土釘加固法[2]。該方法是在小窯采空區上覆巖土鉆斜孔，然后在孔內布置土釘桿體，并沿孔全長注漿。該方法利用土釘的剛度和強度加固上覆巖土[3]，能夠解決小窯采空區地質災害問題，保證上部結構的穩定，不侵占礦產資源，且能保證采礦人員和財產的安全。

采空區的穩定性評價方法主要包括預計法[4-9]、解析法[2，10]、半預計半解析法[11]及數值仿真法[2，12-15]。對于斜土釘加固的小窯采空區，采用了解析法和數值仿真法，具體為基于土釘加固的太沙基土拱理論和有限元法的強度折減法[2]。該文獻假設小窯采空區巖土的參數協調折減。然而實際工程巖土的參數特征并非協調折減，而是服從各自的概率分布[16]。而且，強度折減法未考慮巷道位置、上部荷載、上部安全等級、土釘強度等因素的變化。因此僅僅通過強度折減法獲得的小窯采空區的穩定安全系數并不能客觀、全面評價小窯采空區的穩定性。

因為實際工程的各參數服從各自的概率分布，所以可采用可靠度評價實際工程的穩定性。采空區的可靠度分析方法主要包括一次二階矩法[17]、響應面法[18]、隨機抽樣法（Monte Carlo法）[19-20]，也可采用隨機有限元法[21]。目前未出現針對斜土釘加固的小窯采空區的隨機抽樣法和隨機有限元法的應用。

為了進一步客觀、全面評價斜土釘加固的小窯采空區的穩定性，本文將在解析法和有限元法的基礎上應用隨機抽樣法，即土釘加固的太沙基土拱理論的隨機抽樣法和隨機有限元法。

1 斜土釘加固法[2]

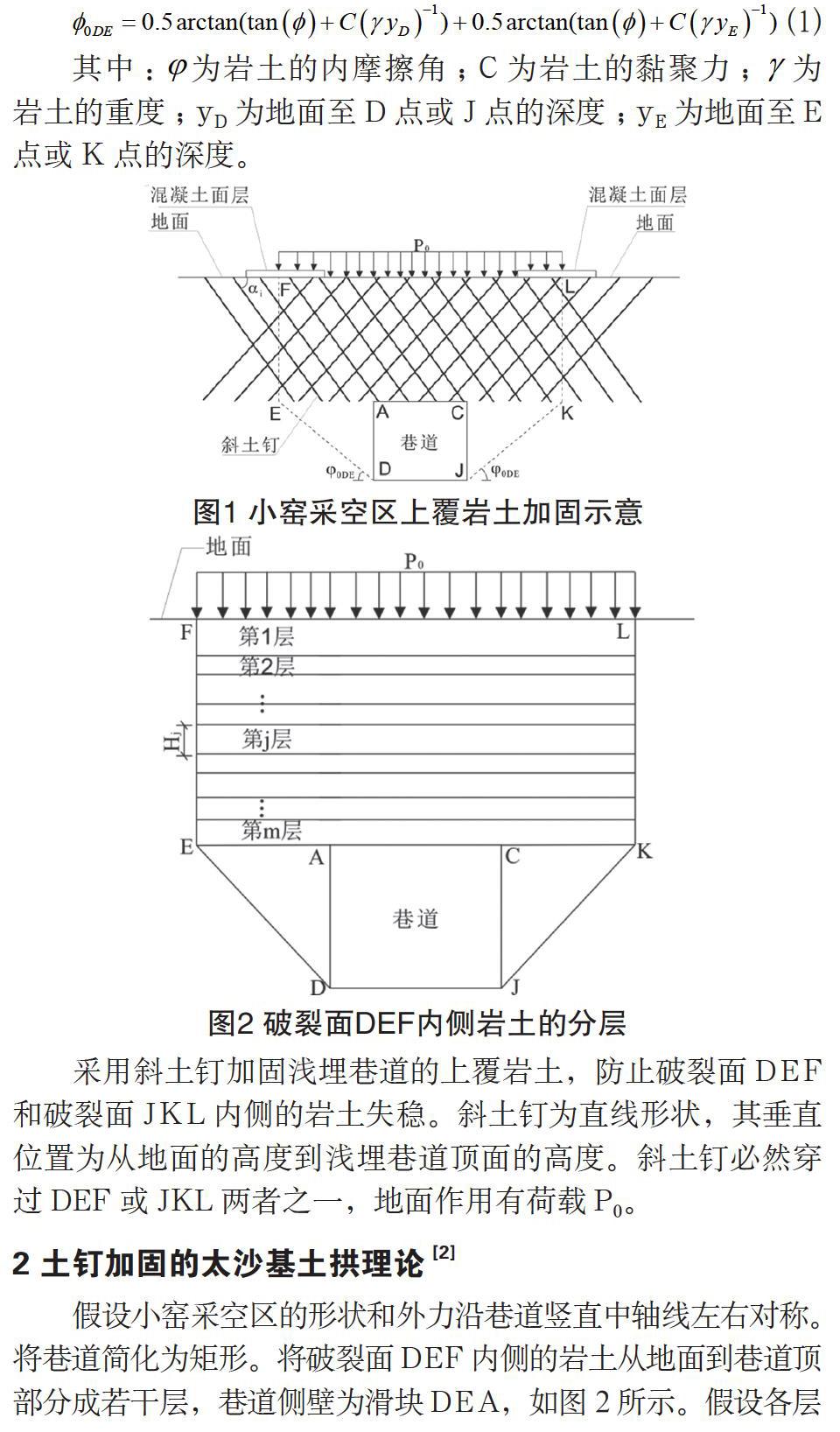
如圖1所示，按照原始太沙基土拱理論[22-23]，淺埋巷道的側壁巖土存在從巷道底面開始的傾斜破裂面DE和JK。DE和JK到達巷道頂部高度后變為豎直破裂面EF和KL直達地面。當巷道完全不加支撐時，DE和JK與水平面的夾角為巖土的平均等效內摩擦角（）[24-25]，即

采用斜土釘加固淺埋巷道的上覆巖土，防止破裂面DEF和破裂面JKL內側的巖土失穩。斜土釘為直線形狀，其垂直位置為從地面的高度到淺埋巷道頂面的高度。斜土釘必然穿過DEF或JKL兩者之一，地面作用有荷載P0。

2 土釘加固的太沙基土拱理論[2]

假設小窯采空區的形狀和外力沿巷道豎直中軸線左右對稱。將巷道簡化為矩形。將破裂面DEF內側的巖土從地面到巷道頂部分成若干層，巷道側壁為滑塊DEA，如圖2所示。假設各層巖土之間的等效內摩擦角不同，但每層內部各點的相等。

考察其中任意一層巖土j。在第j層巖土內部取出一厚度為dHj的水平條帶單元體，如圖3所示。

其中：k0為靜止土壓力系數;為第j層巖土頂面的豎向應力;為D點和E點（或J點和K點）深度的平均等效內摩擦角;為第j層巖土的等效內摩擦角[24-25];Hj為第j層巖土的厚度;b為水平條帶單元體;bt為巷道寬度;Ht為巷道高度;為第j層巖土的等效內摩擦角[24-25];為第j層巖土在垂直破裂面處的抗剪強度;為第j層巖土作用在垂直破裂面上的法向壓力。

式中：n為穿過破裂面且錨固在破裂面兩端巖土的土釘的數量;為土釘釘體的應力強度;Ai為第i根土釘釘體的橫截面面積;為第i根土釘與水平面的夾角;H為所有分層巖土的總厚度。

其中：WDEA為滑塊DEA的自重;FnAE為上覆巖土作用于AE面上的力，方向垂直于AE面法線方向且向下，當FnAE<0時取FnAE=0;m是指緊貼巷道頂面的那一層巖土。當式（9）等號右邊大于1時，滑塊DEA穩定;等號右邊小于1時，滑塊DEA失穩;當式（9）等號成立時，滑塊DEA處于極限平衡式狀態。當滑塊DEA失穩時，滑塊EFLK也難以保持平衡，可認為小窯采空區整體失穩。

3 基于土釘加固的太沙基土拱理論的隨機抽樣法

3.1 基于土釘加固的太沙基土拱理論的隨機抽樣法步驟

本文在評價小窯采空區穩定性時，采用了隨機抽樣法，執行如下步驟：

（1）通過室內試驗、資料搜集、現場調查和數理統計，獲得小窯采空區穩定性因素的統計參數和概率分布，包括巷道位置與尺寸、上部荷載、巖土參數、土釘參數等因素。

（2）每次抽樣按照各因素的統計參數和概率分布類型生成相應的隨機數。當生成的隨機數小于0時，取隨機數為0。

（3）以作為邊界條件，以作為遞推條件，依次循環計算式（1）、（3）、（6）、（5）、（8）（或（7））、（4）、（2），直到最后一層巖土，結束循環。

（4）計算式（10）、（9），并判斷滑塊DEA是否失穩。

（8）當小于目標失效概率[Pf]時評價小窯采空區穩定;當大于[Pf]時評價小窯采空區不穩定。

3.2 目標失效概率

根據《工程結構可靠性設計統一標準GB 50153-2008》對房屋建筑結構構件的可靠指標的規定，結合標準正態分布的定義[26]，本文給出小窯采空區的目標失效概率，如表1所示。

無地基處理的小窯采空區的破壞無預兆，因此地基破壞類型為脆性破壞。土釘屬于柔性材料，能夠提高地基土的柔韌性[3]，因此有土釘加固的小窯采空區的破壞類型可判別為延性破壞。

4 小窯采空區可靠度分析的隨機有限元法

小窯采空區可靠度分析的隨機有限元法與常規的隨機有限元法[21]無太大差異，是有限元法[27]與隨機抽樣法[20]的結合。

5 算例

算例包括基于土釘加固的太沙基土拱理論的隨機抽樣法分析小窯采空區可靠度和隨機有限元法分析小窯采空區可靠度。

5.1 基于解析法的隨機抽樣法分析小窯采空區可靠度

某小窯采空區[2]穩定性的因素的統計參數和概率分布類型見表2、表3。抽樣時，按照表中的統計參數和概率分布類型生成相應因素的隨機數。其中的nd為穿過破裂面且錨固在破裂面兩端巖土的土釘的設計數量。ns指穿過破裂面且錨固在破裂面兩端巖土的土釘的施工次品數量。生成隨機數法方法詳見有關抽樣技術的文獻[28]。

每次抽樣的粘聚力C按照式（13）計算[2]。式（13）為某小窯采空區的土在結構性發生變化時與C所呈現出的函數關系，該式由室內試驗測得的與C擬合得到，當C<0時，取C=0。

將表2、表3的參數以及式（13）應用到4.1節基于土釘加固的太沙基土拱理論的隨機抽樣法步驟中去，評價小窯采空區的穩定性。

評價結果：對于無地基處理情況，地基脆性破壞，太沙基破裂面內側巖土的失效頻率為0.007111，高于安全等級為一級、二級和三級的上部結構的目標失效概率[pf]，因此對于一級、二級和三級的上部結構來說小窯采空區不穩定。對于有土釘加固情況，地基延性破壞，為0.000569，高于安全等級為一級的上部結構的[pf]，因此對于一級的上部結構來說小窯采空區不穩定;但低于安全等級為二級、三級的上部結構的[pf]，因此對于二級、三級的上部結構來說小窯采空區穩定。

5.2 隨機有限元法分析小窯采空區可靠度

有限元建模與求解方法與文獻[2]相同。采用隨機有限元法[21]分析小窯采空區的穩定性。分析過程中，按照表2和表3的統計參數和概率分布類型以及式（13）生成每次抽樣的相應因素的隨機數。以位移—荷載曲線發生突變作為有限元極限狀態的判據。按照式（11）計算每次抽樣的指示函數IF。循環抽樣并分析，直到達到總的抽樣次數Nn。按照式（12）計算太沙基破裂面內側巖土的失效頻率。

評價結果：對于無地基處理情況，為0.007038;對于有土釘加固情況，為0.000673。隨機有限元法仿真得到的失效概率和基于土釘加固的太沙基土拱理論的隨機抽樣法計算得到的失效概率差別不大。

6討論

根據隨機抽樣法原理[20]，當Nn趨于無窮大時，趨近于Pf。Nn越大，的計算結果越穩定。要達到一定的精度， Nn必須取得足夠大。本文建議，對于安全等級為一級的上部結構，Nn不小于235416;對于安全等級為二級的上部結構，Nn不小于41945;對于安全等級為三級的上部結構，Nn不小于9596。

有土釘加固的小窯采空區比無地基處理的小窯采空區的穩定安全系數高[2];有土釘加固的小窯采空區比無地基處理的小窯采空區的可靠度高。因此隨機抽樣法和強度折減法[2]評價小窯采空區穩定性的結果具有一致性。

強度折減法[2]假設工程的材料強度參數折減;隨機抽樣法通過室內試驗、資料搜集、現場調查和數理統計獲得實際工程穩定性因素的統計參數和概率分布。而且，強度折減法[2]未考慮上部結構的安全等級和地基的破壞類型;隨機抽樣法的目標失效概率受上部結構的安全等級和地基的破壞類型的影響。綜上所述，隨機抽樣法是立足于客觀現象的方法，考慮的因素更全面，因此通過隨機抽樣法獲得的斜土釘加固小窯采空區的穩定性評價結果，比強度折減法更有說服力。

7 結論

本文在解析法和有限元法的基礎上應用隨機抽樣法，即土釘加固的太沙基土拱理論的隨機抽樣法和隨機有限元法，評價了斜土釘加固的小窯采空區的穩定性。由此得出以下結論：

（1）小窯采空區的目標失效概率與上部結構的安全等級和地基的破壞類型有關。

（2）基于土釘加固的太沙基土拱理論的隨機抽樣法計算得到的失效概率和隨機有限元法仿真得到的失效概率差別不大。

（3）通過隨機抽樣法獲得的斜土釘加固小窯采空區的穩定性評價結果，比強度折減法更有說服力。

參考文獻

[1] 趙忠海.地球物理探測技術在北京門頭溝小窯采空區勘查中的應用[J].中國地質災害與防治學報，2010，21（1）：60-64.

[2] 馬少坤，李濤，邵羽.小窯采空區淺埋巷道上覆巖土土釘加固分析[J].廣西大學學報（自然科學版），2018，43（4）：1455-1465.

[3] 龔曉南.土釘和復合土釘支護若干問題[J].土木工程學報，2003，36（10）：80-83.

[4] 郁文峰，陳元非，孟彥杰，等.鄰近采空區影響的地表沉陷概率積分參數反演[J].煤礦安全，2019，5（5）：231-234+238.

[5] 喬元鋒.運用典型曲線法做好涼水井煤礦沉陷參數計算[J].內蒙古煤炭經濟，2016，1（16）：144-145+153.

[6] 王正帥，鄧喀中.老采空區殘余沉降的離散灰色預測模型[J].煤炭學報，2010，35（7）：1084-1088.

[7] 郝剛，于啟升.穩健統計方法在老采空區沉降數據處理中的應用[J].現代礦業，2010，26（2）：76-78.

[8] 戴華陽.地表移動預計的新設想——采空區矢量法[J].礦山測量，1995，1（4）：30-33+24.

[9] 孫宇超，趙周能，陳星明，等.基于AHP和模糊數學方法的采空區穩定性評價[J].有色金屬（礦山部分），2019，71（5）：35-40.

[10] 高曉輝，彭建兵，楊天亮，等.西合高速公路采空區穩定性評價及其治理方案[J].地球與環境，2005，33（3）：139-141.

[11] 馮遠建，李子龍.礦山采空區穩定性分析及安全治理方法研究[J].煤炭與化工，2014，37（6）：28-30.

[12] 妙美蘭，寥英泰，鄒澤舉.基于彈性非線性理論的采空區有限元數值模擬分析[J].西部探礦工程，2005，17（11）：104-106.

[13] 楊素春.潭山鉛鋅礦地下采空區斷層切割的邊坡穩定性邊界元法分析[D].上海：同濟大學，1990.

[14] 王秀格，喬蘭，孫歆碩.地下采空區上輸電塔基穩定性的數值模擬[J].金屬礦山，2008，1（3）：110-113+143.

[15] 李一帆，李作良，王慧萍.城市固體廢棄物充填采空區的離散元分析[J].礦業安全與環保，2009，36（5）：12-14+17.

[16] 鄭軼軼，朱劍鋒，劉干斌，等.寧波軟土物理力學參數概率分布及相關性研究[J].中國科技論文，2013，8（5）：367-373.

[17] 張耀平.礦山空區誘發的巖移特征及覆蓋層冒落效應研究[D].長沙：中南大學，2010.

[18] 徐晨浩，張衛東.基于新型響應面法的煤礦采空區坡沿隆起風險分析[J].武漢理工大學學報，2017，1（12）：56-61.

[19] 程涌，劉建龍，楊八九.蒙特卡洛法在采空區穩定性分析中的應用研究[J].銅業工程，2017，1（2）：27-30.

[20] 張建中.蒙特卡洛方法（Ⅰ）[J].數學的實踐與認識，1974，1（1）：28-40.

[21] 王建軍，于長波，李其漢.工程中的隨機有限元方法[J].應用力學學報，2009，26（2）：297-303.

[22] Terzaghi K..Rock Defects and Loads on Tunnel Support[M].Massachusetts：Harvard Univ，1946.

[23] Son M..Three-Dimensional Expansion of the Terzaghi Arching Formula Considering Inclined Sliding Surfaces and Examination of Its Effects[J].International Journal of Geomechanics，2017，17（7）：06016043.

[24] 周旋.等效內摩擦角計算方法及其應用[J].水運工程，2016，41（7）：22-25.

[25] Protodyakonov M. M..Methods of Studying the Strength of Rocks[C].Mining Research，Missouri：Pergamon Press，1962：649-668.

[26] 梁昌洪，李龍，史小衛.標準正態分布的簡潔閉式[J].西安電子科技大學學報（自然科學版），2003，30（3）：289-292.

[27] 王勖成.有限單元法[M].北京：清華大學出版社，2003.

[28] 沈華韻，張鵬，王侃.改進線性同余法隨機數發生器[J].清華大學學報（自然科學版），2009，49（2）：191-193.