全模顫振雙索懸掛系統剛體模態頻率研究
吳太歡,林麒,何升杰,柳汀,高忠信,王曉光
廈門大學 航空航天學院, 廈門 361102
顫振問題是氣動彈性研究領域的重要分支。利用動力學縮比模型在風洞中開展顫振試驗,能夠較為準確地模擬飛行器的顫振現象[1-3]。風洞顫振試驗一直以來是分析和驗證飛行器顫振特性的重要手段。風洞顫振試驗分為部件顫振試驗和全機模型顫振試驗。只做部件顫振試驗,無法獲得全機顫振的特性,不能完全滿足現代飛行器設計與研發的需求,因此,進行全機模型顫振試驗是非常有必要的[4]。全機模型風洞顫振試驗除了對模型本身的設計和加工要求苛刻之外,對于模型支撐系統也提出了特殊的要求。如何設計出功能強大,滿足各類飛行器全機模型風洞顫振試驗需求的支撐系統是當前風洞試驗研究領域的重要課題[5-6]。NASA蘭利風洞試驗中心早在20世紀五六十年代就開始開展全機模型顫振試驗,研發了多套性能優異的模型系統,其中包括雙索懸掛系統[7-8]。中國空氣動力研究與發展中心2004年在2.4 m亞跨超風洞中引進俄羅斯的懸浮系統FSS(Float Suspension System)技術,并將其工程化,應用于全模顫振試驗,促進了國內風洞顫振試驗研究的發展與進步。但是懸浮系統運用于靜不穩定的飛行器時,試驗效果不理想,無法完全滿足當下的風洞顫振試驗需求[5-6,9]。面對風洞全模顫振試驗的迫切需求,有必要研制一套或多套功能強大、通用性好的顫振試驗系統。而雙索懸掛系統作為一種通用性強、試驗性能優異的全機模型顫振試驗支撐系統,能夠做到適用于靜不穩定飛行器,具有較好的應用前景[1]。
為在風洞中模擬飛行器真實飛行過程中的顫振現象,要求模型支撐系統對全機模型釋放5個自由度,僅約束風洞來流方向的自由度,且支撐的剛體模態頻率盡可能低至模型固有頻率的1/10~1/3,做到對模型本身的結構動力學干擾小、對模型的氣動力干擾小[2,8,10-11]。
劉基海等采用理論計算和試驗相互驗證的方法研究了彈簧支撐的支撐剛度對飛翼模型固有模態和體自由度顫振特性的影響規律[12];王大鵬和蔡駿文分析了橡皮繩懸掛系統的不同懸掛剛度、不同懸掛位置對細長體飛行器模態試驗結果的影響[13]。研究雙索懸掛系統剛體模態頻率變化規律及其影響因素,能夠為雙索懸掛系統的優化設計提供依據。
本文基于繩索并聯機構理論建立了雙索懸掛系統靜力學模型,引入加權矩陣,推導了雙索懸掛系統靜剛度模型;建立了雙索懸掛系統模型無阻尼振蕩方程,分析了雙索懸掛系統剛體模態頻率隨繩索預緊力的變化規律;搭建了雙索懸掛系統地面樣機,開展系統剛體模態頻率測試試驗,研究雙索懸掛系統繩索預緊力和繩系結構對系統剛體模態頻率的影響規律。
1 繩索并聯機構靜力學分析
全模顫振風洞試驗要求模型的支撐只對來流方向加以約束,其他5個自由度盡可能地釋放開,做到模型在吹風試驗中盡可能地處于與真實飛行時相同的自由狀態,以實現顫振試驗的動力學相似。
根據上述要求,本文設計和研究的全模顫振雙索懸掛系統主要由豎直繩索、水平繩索、繩索收放裝置以及輔助繩索和相應的控制部件等組成,如圖1所示。
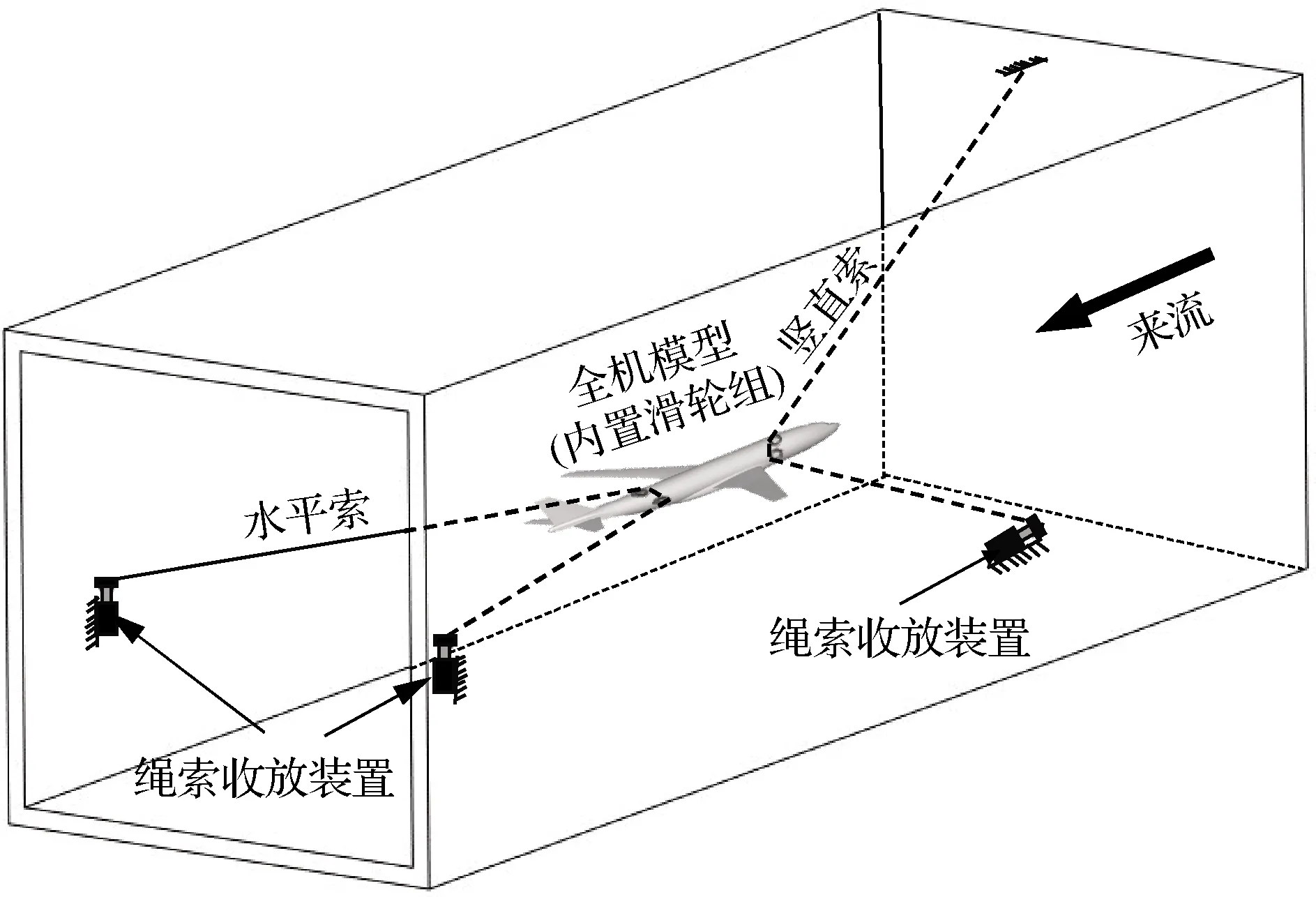
圖1 雙索懸掛系統示意圖Fig.1 Sketch of two cables suspension system
穿過模型機身后部水平滑輪的水平繩索的左右兩支形成一定張角,一端連接到風洞左壁上的繩索收放裝置,另外一端過后機身滑輪連接到風洞右壁上的繩索收放裝置;穿過模型機身前部豎直滑輪的豎直繩索位于飛行器機體軸所在的豎直面內,上下兩支形成一定張角,上端固連在風洞上壁板,下端過飛機模型前滑輪連接到下壁板上的繩索收放裝置;通過繩索收放裝置控制繩索張緊力和繩索長度,雙索懸掛系統能夠將飛行器模型穩定地支撐在風洞試驗段。全模顫振雙索懸掛系統是一種欠約束的繩索并聯支撐機構。本節根據繩索并聯機構靜力學理論,建立雙索懸掛系統飛行器模型的靜力學模型。
1.1 幾何關系
為描述全模顫振雙索懸掛支撐系統中飛行器模型的運動與支撐機構的關系,建立靜、動2個坐標系,如圖2所示。圖中粗直桿為模擬機身,機身上的兩短桿分別為前后滑輪支架。
建立在模型上的坐標系為動坐標系(即機體坐標系)Obxbybzb,坐標原點Ob與飛機模型(即末端執行器)的質心P0重合,Obxb軸位于飛機模型的對稱面內并與機體主軸重合,正方向指向機頭;Obzb軸也位于飛機模型對稱面內,垂直于Obxb軸并指機身下方;Obyb垂直于飛機模型的對稱面,指向飛機模型的右舷方向,其方向遵循右手定則。
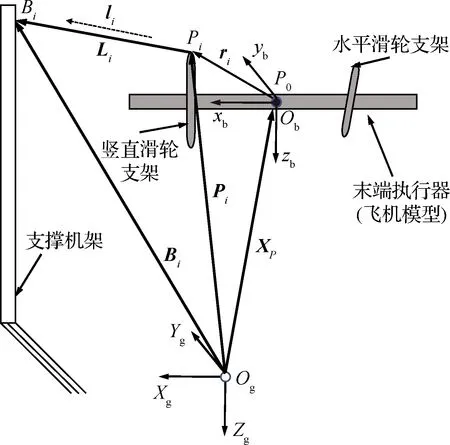
圖2 繩索并聯機構運動學示意圖Fig.2 Sketch of cable driven parallel mechanism kinematics
靜坐標系建立在機架上,相對地面固定,也稱為地面坐標系。在機架上取任意一點作為地面坐標系OgXgYgZg的原點Og,OgZg軸豎直向下指向地心,OgXgYg平面垂直于OgZg軸;OgXg垂直于OgZg軸指向風洞試驗來流方向;OgYg軸垂直于OgXg軸,方向遵循右手定則。矢量XP是機體坐標系原點Ob在地面坐標系中的位置矢量。
為分析方便,又不失一般性,假設各繩索均與飛機模型固連。Li是第i根繩索連接末端執行器鉸點Pi與機架上固定鉸點Bi之間的矢量。
Li=Bi-(XP+Rri) ?i=1,2,…,n
(1)
式中:n由牽引繩的數量決定;R是機體坐標系到地面坐標系的旋轉轉換矩陣,具體表示為
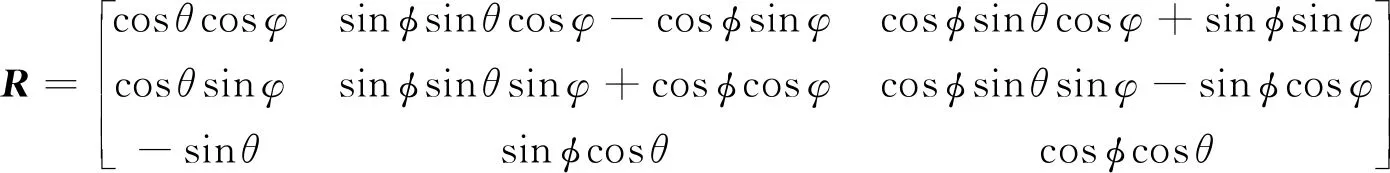
其中:φ、θ、φ分別表示飛機模型在地面坐標系中繞OgXg軸、OgYg軸和OgZg軸旋轉的滾轉角、俯仰角和偏航角。
繩索矢量方程(1)的2范數即為第i根繩索的長度:
(2)
對方程(1)求時間導數得到[14]
(3)
(4)
式中:JA表示繩系并聯機構的Jacobian矩陣;X是末端執行器的位姿參數[14-15]。
1.2 靜力平衡關系
圖3為繩索并聯機構靜力平衡示意圖,末端執行器受繩索拉力Ti作用,同時受外力fe、外力矩τe以及末端執行器重力mg作用,處于靜平衡狀態。根據Newton-Euler法能夠得到末端執行器的靜平衡方程為
(5)
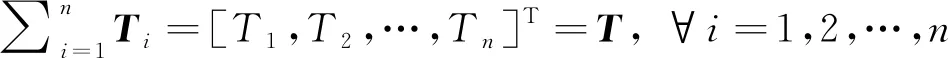
(6)

圖3 繩索并聯機構靜力學示意圖Fig.3 Sketch of cable driven parallel mechanism static
末端執行器的剛度定義為在單位外力作用下末端執行器的位姿變化,數值上等于使系統產生單位位姿變化所需要的外力值[14-16]。因此,對方程(6)求末端執行器的位姿偏導數,得到繩系并聯機構剛度矩陣:
(7)
忽略繩索的質量,將繩索假設為無質量無阻尼的彈簧;同時,假設末端執行器為剛體,忽略末端執行器的變形,系統剛度矩陣可以展開為
(8)

其中:diag(k1,k2,…,kn)表示繩系剛度對角陣,ki為第i根繩索的剛度,因此:
(9)
將剛度矩陣表示為
K=KT+KK
(10)
式中:K為系統總剛度;KT為與繩索拉力和繩系結構相關的剛度矩陣;KK為與繩索剛度相關的剛度矩陣[15]。具體形式為
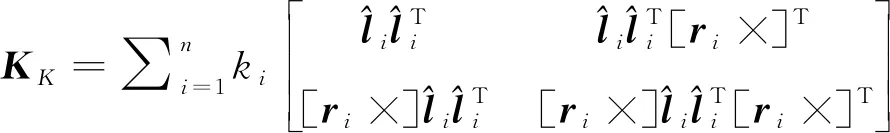
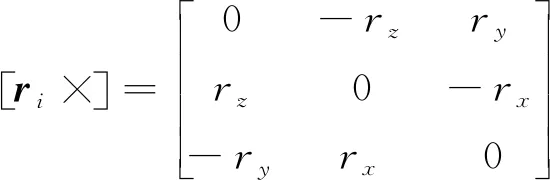
λj>0, s.t det(K-λjI)=0
式中:λj為剛度矩陣第j階特征值,?j=1,2,3,…;m 基于雙索懸掛系統基本構型,在實驗室搭建地面縮比樣機,如圖4所示。采用60 mm×60 mm 的鋁合金型材搭建地面樣機機架,模擬風洞試驗段。 參考常見的民機外形設計加工了第1代飛機模型(見圖5),模型質量為1.61 kg。因為只做原理性研究,不用于風洞吹風,故機頭簡化加工成半球狀。在ANSYS中分析得到飛機模型的固有頻率,見表1。 圖4 雙索懸掛系統地面樣機Fig.4 Ground prototypr of two cables suspension system 表1 第1代飛機模型的固有頻率Table 1 Natural frequencies of the first aircraft model 文中凡與滑輪有關的距離,均相對于滑輪的軸心而言。圖5(a)中,ζ1為機身前滑輪與模型質心之間的距離,ζ2為機身后滑輪與模型質心之間的距離;在模型的前部和后部分別設計了用于安裝滑輪的支架,圖5(b)為滑輪支架。 雙索懸掛系統的繩索選材為直徑0.8 mm的8股Kavlar線,其彈性模量為42.8 GPa。豎直繩索和水平繩索分別穿過機身前部和后部的滑輪,懸掛起飛行器模型。各繩在滑輪后分開的兩支分別經機架上下部和左右側的轉向滑輪連接到拉力傳感器上。拉力傳感器安裝在電機驅動的滾珠絲杠的滑塊上,用于測量繩索張力,滾珠絲杠在電機的驅動下帶動滑塊做直線運動,從而調控繩索拉力和繩長。 圖5 簡化的民機模型及機身滑輪支架Fig.5 Simplified model of civil aircraft and support system of pulleys 為研究雙索懸掛系統的剛體模態頻率,需要先分析系統的靜剛度,為此將雙索懸掛系統簡化為空間四索并聯機構,如圖6所示。同時假設豎直繩索與水平繩索都分成兩支,分別與飛行器模型(末端執行器)固連,且處于靜力平衡狀態。這個假設提高了系統的靜剛度,分析所得雙索懸掛系統的剛體模態頻率會比實際情況偏高些。 圖6中:P1、P2分別為豎直繩索與前機身的鉸接點(實際是與機身前部滑輪的接觸點),P3、P4分別為水平繩索與后機身的鉸接點(實際是與機身后部滑輪的接觸點),P0為模型質心;B1、B2分別為豎直繩索與機架上下的鉸接點,B3、B4為水平繩索與機架兩側的鉸接點。 以上豎直繩索和水平繩索與模型及機架的鉸接點坐標列于表2中。其中,Pi點坐標取各機身滑輪軸心坐標值;繩索長度遠大于安裝在地面樣機上的模型機身內的滑輪直徑和機架上的滑輪直徑,因此,上述簡化方法對計算分析的結果影響不大。 由1.2節中得到的繩索并聯機構靜力平衡方程式(5)也適用于雙索懸掛系統。根據雙索懸掛系統繩系的特點,式(5)中的n取4。 雙索懸掛系統的繩索穿過機身滑輪將飛行器模型懸掛起來,繩索與飛行器模型之間是一種接觸式約束,而非固連式約束,為了在數學上等效滑輪的作用,參考滑輪動力學理論引入剛度矩陣KT的加權矩陣ET和剛度矩陣KK的加權矩陣EK,于是,得到雙索懸掛系統剛度矩陣的經驗公式[19-21]: 圖6 空間四索并聯機構簡圖Fig.6 Sketch of space four wires parallel mechanism 表2 雙索系統繩索與機構連接點的坐標 K=ETKT+EKKK (11) 繩索過滑輪懸掛飛機模型,預緊力的變化勢必影響懸掛系統的剛度,又由于繩索實際是繞過滑輪而并非固連在滑輪支架上,其變形對懸掛系統轉動剛度的影響被機身滑輪抵消,但其對系統平動剛度影響依然存在,這些因素的影響程度事先無法準確判定。因此,對兩個加權矩陣先以假設初值代入(如式(12)、式(13)所示),并以ET0和EK0表示,后續再參考試驗數據對其進行修正,以獲得較準確的剛度模型。 (12) (13) 另外與繩拉力相關的剛度矩陣KT和與繩索剛度相關的剛度矩陣KK表示為 (14) (15) 雙索懸掛系統的地面樣機飛行器模型質心在地軸系中的坐標值為P0=(0,0,-0.416),設ζ1=ζ2=70 mm,利用MATLAB編程仿真。首先根據系統靜力平衡方程計算繩索預緊拉力,得到T={65.6 N,65.6 N,57.4 N,57.4 N},前兩個元素即為豎直繩預緊力,后兩個元素為水平索的預緊力;然后將所有參數代入式(14)、式(15)和式(11) 中,計算得到與繩索預緊拉力相關的剛度矩陣KT、與繩索剛度相關的剛度矩陣KK以及系統總剛度K和系統總剛度矩陣主對角線組成的剛度對角陣為 KT= (16) 上述6個值分別表示模型沿OgXg軸、OgYg軸、OgZg軸的平動剛度和繞OgXg軸、OgYg軸、OgZg軸的轉動剛度[14]。顯然,OgXg方向的剛度最大,比沿OgYg、OgZg方向的平動剛度大1個數量級,比繞OgXg軸、OgYg軸、OgZg軸的轉動剛度大3個數量級。 式(16)中各自由度上的剛度大小反應了支撐系統對模型的約束情況,即該懸掛系統在模型的3個轉動自由度上約束最小,而橫向與沉浮方向的約束次之,驗證了雙索懸掛系統符合全模顫振試驗支撐釋放除來流方向(即OgXg方向)以外的5個自由度的設計要求。這表明,圖1的全模顫振雙索懸掛支撐在理論上是合理的。 在建立系統靜力學模型時,已經假設繩索質量忽略不計,且始終處于受拉狀態,同時假設飛行器模型是一個剛體。基于這些假設,進一步建立雙索懸掛系統無阻尼彈簧-振子振動模型: (17) (18) 式中:ηq為系統剛度矩陣第q階特征值,進一步得到系統第q階模態的固有頻率fq: (19) 式中:Kqq為系統剛度矩陣K第q行q列元素值;Mqq為飛行器模型慣性矩陣M第q行q列元素值。 如上所述,全模顫振雙索懸掛系統應能夠釋放模型俯仰、偏航、滾轉、升沉及側滑等5個方向自由度。飛行器模型在雙索懸掛系統支撐下進行顫振試驗,系統剛體模態的固有頻率大小是決定試驗成功與否的重要因素之一[22]。 系統剛體模態頻率是衡量雙索懸掛系統整體性能的指標之一。假設雙索懸掛系統繩索預緊力從15 N逐漸增大到200 N左右,根據式(11)~式(15)以及式(19),計算在雙索懸掛系統支撐下模型各階剛體模態的固有頻率。 實驗室里對地面樣機的測試結果表明,當模型處于靜力平衡狀態時,雙索懸掛系統的豎直繩索預緊拉力和水平繩索預緊拉力在數值上差異較小,因此不失一般性地,在下面的分析中用豎直繩索和水平繩索的預緊拉力平均值描述懸掛系統的繩索預緊拉力,整體性地研究繩索預緊拉力對系統剛體模態頻率的影響。 圖7給出了理論計算得到的系統各剛體模態頻率受繩索預緊力影響的規律。表3則給出了具體數值。當繩索預緊拉力為60 N左右時,計算所得系統剛體模態頻率的分布與系統靜剛度分析的結果式(16)在規律性上是一致的。 圖7 固有頻率隨繩索預緊力變化曲線(理論)Fig.7 Natural frequencies vary with ropes tension (theoretical) 表3 固有頻率隨繩索預緊力變化Table 3 Natural frequency variations with ropes tension 由圖7可知,系統剛體模態的固有頻率隨繩索預緊力增大而增大,但隨繩索預緊力增長的速率不同,轉動模態的固有頻率受繩索預緊力的影響比平動模態大得多。 在圖7中,系統各剛體模態頻率都保持在相對較低的頻率范圍內(<13 Hz)。其中,最大的剛體模態頻率約為模型固有頻率(一階固有頻率為38.561 Hz)的1/3,最小的剛體模態頻率約為模型固有頻率的1/10,符合全模顫振試驗對模型支撐的要求。 轉動模態方面,在一定繩索預緊力范圍內,滾轉模態的固有頻率最大且隨繩索預緊力增長的速率最快,俯仰模態的固有頻率最低且隨繩索預緊力增長最慢。平動模態方面,固有頻率隨繩索預緊力增大略微有增長,但是數值變化很小,且側滑模態的固有頻率略小于升沉模態的固有頻率。 雙索懸掛系統在OgXg方向的平動固有頻率保持在20 Hz以上(圖、表中未給出),遠高于其他自由度的固有頻率,體現了系統能夠約束模型在來流方向的自由度,釋放其他5個方向自由度的特點。 下面通過地面樣機模態頻率測試試驗,一方面考察雙索懸掛系統剛體模態頻率的變化規律以驗證理論分析的結果,另一方面通過試驗探究繩系結構對雙索懸掛系統剛體模態頻率的影響,深入了解雙索懸掛系統的力學特性,為理論剛度模型的修正提供可靠的數據。 在地面樣機上采用錘擊法進行模態頻率測試試驗[23]。調整機身前、后滑輪與模型質心之間的距離為ζ1=ζ2=70 mm、機身前后滑輪總距離為ζ=ζ1+ζ2=140 mm。兩個加速度計A、B分別固定于模型機身的前后部位(見圖8)。4個拉力傳感器分別兩兩串接于豎直繩索和水平繩索處于滑輪兩側的兩支。其中,傳感器1、2分別串接于豎直繩索的兩支,而傳感器3、4分別串接于水平繩索的兩支。 圖8 模態頻率測試試驗Fig.8 Modal frequency test experiment 進行錘擊試驗時,在對豎直繩索和水平繩索施加一定預緊拉力的情況下,用力錘沿某一自由度方向敲擊模型,激勵模型自由振蕩;繩索拉力因此發生變化,用串聯在豎直繩索和水平繩索兩端的拉力傳感器測量繩索拉力響應信號;同時用粘附在模型上的加速度計測量模型的加速度響應信號。采集上述測量數據,再將繩索拉力響應和加速度響應信號分別進行傅里葉變換,可以得到該自由度方向的幅頻特性。 按照上述方法,在不同繩索預緊力條件下,重復試驗采樣,獲得足夠的試驗數據進行分析,可獲得相應試驗條件下雙索懸掛系統剛體模態頻率變化規律。 下面給出通過試驗得到的雙索懸掛系統對錘擊激勵的響應,以及繩索預緊力對系統剛體模態頻率的影響。 圖9為當豎直繩索預緊力為47.2 N、水平繩索預緊力為42.3 N時,模型受俯仰方向的錘擊激勵做自由振蕩過程中采集到的繩索拉力響應和加速度響應信號。從圖9 (a)中可見,機身前后兩個加速度計的響應信號相位相反,且機身后部加速度響應幅值大于前部。在圖9(b)中,水平繩索拉力的響應幅值略大于豎直繩索拉力。 分別對上述響應信號做傅里葉變換,可得到各自的頻域特性曲線,如圖10所示,頻率響應曲線的一階模態模型對應激勵方向上剛體模態的固有頻率。 圖10(a)為加速度幅頻曲線,機身前部響應幅值小于機身后部響應幅值,但是對應的峰值頻率相同;圖10(b)為繩索拉力幅頻曲線,繩索串接的4個拉力傳感器的響應信號中各階頻率一致性很好,且繩索拉力響應幾個峰值頻率都與圖10 (a) 相同。這表明繩索拉力響應信號和加速度響應信號都能夠較為準確地反應雙索懸掛系統的剛體模態頻率。 圖9 繩索拉力響應和加速度響應Fig.9 Rope tension responses and acceleration responses 圖10 加速度響應和繩索拉力響應頻譜Fig.10 Acceleration responses and ropes tension responses spectra 改變繩索的預緊力,從15 N逐漸增長到200 N左右,測試每一組繩索預緊力下系統各剛體模態頻率的大小,結果如圖11所示。 圖11的模態頻率測試結果表明系統剛體模態頻率隨繩索預緊力的增大而升大,但都保持在較低的頻率范圍內(均不大于10 Hz)。各階剛體模態的固有頻率隨繩索預緊力增加的速率各異。轉動模態的固有頻率受繩索預緊力的影響比平動模態大得多。在轉動模態方面,在試驗的繩索預緊力范圍內,滾轉模態的固有頻率最大且增長最快,俯仰模態的固有頻率最小且增長最慢;平動模態的固有頻率隨繩索預緊力增大略微有增長,但是量值很小,且橫側向模態的固有頻率略小于升沉模態的固有頻率。 在圖7和圖11中,雙索懸掛系統在繩索預緊力小的情況下,升沉和橫側向的剛體模態頻率都較高(5~9 Hz),其根本原因在于繩系對模型的約束方式。雙索中的豎直繩索對模型的沉浮方向施加了約束,而水平繩索對模型的橫側向方向施加了約束。受約束越大的方向,剛度越大,剛體頻率也越高。另一方面,在算例式(16)中,雙索懸掛系統的平動剛度比轉動剛度大兩個數量級,剛度越大的方向,對應的剛體模態頻率也會越高。 雖然機身內設置了滑輪,有助于釋放平動自由度,但是作用效果有限。當繩索預緊力較小時,對地面樣機上的模型,用手施加激勵,在3個轉動自由度方向,模型都很容易發生來回轉動,說明剛度較低,對應的剛體頻率也低;而在升沉和橫側向兩個方向,剛度較大,需要施加較大的激勵,才能使模型有較大的位移幅度。這表明這兩個平動自由度方向的剛體模態頻率較高。 圖11 固有頻率隨繩索預緊力變化曲線(試驗)Fig.11 Natural frequency with ropes tension (experimental) 對比圖7的理論仿真結果和圖11的試驗測試結果可知,雙索懸掛系統各階剛體模態對應的固有頻率隨繩索預緊力變化的規律是相同的,均隨繩索預緊力增大而升高,且分布規律和增長趨勢相同。但是,理論仿真結果和試驗測試結果在數值上存在一定差異,其相對誤差ef可表示為 (20) 圖12為各階剛體模態的固有頻率理論值和試驗值之間的誤差曲線。顯然,如2.2節中的預測,理論仿真結果普遍大于試驗測試結果。當繩索預緊拉力足夠大時(在本文中,T>80 N)各剛體模態頻率的理論分析值與試驗值的相對誤差基本不變,繩索預緊拉力的影響主要是在其值較小時。 分析理論仿真結果與試驗測試結果之間誤差值ef的大小和分布關系,對加權矩陣進行修正: 得到新的系統剛度矩陣計算式為 K=ET1KT+EK1KK (21) 圖12 理論結果與試驗結果誤差率曲線Fig.12 Error rate curves between theoretical and experimental results 在此基礎上重新進行理論仿真,得到系統剛體模態頻率與試驗值之間的誤差降低到5%以內。因此,本文的理論建模方法是合理可行的。通過修正加權矩陣,仿真計算得到的系統剛體模態頻率隨繩索預緊力增長的趨勢與試驗結果一致,且各階剛體模態固有頻率的大小關系和分布規律與試驗結果高度吻合。上述方法具有一定指導意義,可以為后續理論模型的修正提供參考。 前述主要研究繩索預緊拉力對雙索懸掛系統剛體模態頻率的影響,下面討論繩系結構的影響。這里,繩系結構的變化主要反映在機身滑輪位置的不同設置上。 2.1節中定義ζ1、ζ2為機身前后滑輪與模型質心之間的距離,兩滑輪總間距為ζ=ζ1+ζ2。本節再定義機身前后滑輪到模型質心距離的比值為δ=ζ1/ζ2。δ和ζ、ζ1、ζ2均為雙索懸掛系統的結構參數,研究它們對系統的各階轉動模態固有頻率的影響具有重要意義。 令機身前后滑輪關于模型質心對稱布置,即δ=1,且機身前后滑輪間距ζ分別為134 mm、154 mm、174 mm,改變繩索預緊力,從15 N逐漸增長到200 N左右,測試每一組繩索預緊力下系統各剛體轉動模態頻率的大小。試驗結果如圖13 所示。 由圖13可知,3種滑輪間距下各轉動模態的固有頻率隨繩索預緊力變化速率基本均無差異。繩索預緊力在100 N以內,懸掛系統的各剛體模態頻率基本能夠維持在8 Hz以下(結合圖11)。上述結果表明:當滑輪軸心距比例系數δ=1,即機身前后滑輪相對于質心對稱布置,與質心的距離ζ1、ζ2相同時,系統剛體轉動模態頻率隨繩索預緊力變化趨勢與機身前后滑輪的間距ζ無關。也就是說這時繩索預緊力對系統剛體轉動模態頻率幾乎沒有影響。 令機身前、后兩滑輪間距為ζ=134 mm,滑輪距比例系數δ=0.54,1,1.89,即機身前后滑輪關于模型質心成不對稱布置,再進行上述試驗測試。 試驗結果如圖14所示。雙索懸掛系統剛體轉動模態頻率仍隨繩索預緊力增大而增大,但各轉動模態的固有頻率變化不同。 圖13 固有頻率隨繩索預緊力變化曲線(δ=1)Fig.13 Natural frequency curves with rope tension of cable (δ=1) 圖14 固有頻率隨繩索預緊力變化曲線(ζ=134 mm)Fig.14 Natural frequency curves with rope tension of cable (ζ=134 mm) 在圖14(a)中,俯仰模態的固有頻率受δ的變化影響最大。當δ>1時,俯仰模態頻率較δ=1時小;當δ<1時,俯仰模態頻率較δ=1時大。這表明,當前機身滑輪距離質心較后機身距離質心遠時,俯仰模態頻率減小,反之亦然。由圖14(b)可知,偏航模態固有頻率的變化趨勢是相反的。由此可以判定:機身前后滑輪到模型質心距離的比值δ是影響模型俯仰、偏航模態的固有頻率的重要因素之一。但是在圖14(c)中,滾轉模態頻率對δ的變化分散性很小,幾乎不受δ的影響,或者說,滾轉模態頻率與機身前后滑輪的位置基本無關,僅與繩索預緊力有關,但是繩索預緊力對滾轉模態頻率的影響比對其他兩個轉動模態的頻率大。 在本文的試驗條件下,系統剛體轉動模態頻率隨繩索預緊力的增加而上升;當繩索預緊力小到一定水平(大約20 N)時,系統剛體轉動模態頻率的水平較低,可降到2~3 Hz左右,前后滑輪軸心距ζ對系統剛體轉動模態頻率的影響不顯著。 繩索預緊力T、機身前后滑輪到模型質心距離的比值δ是系統剛體模態頻率的重要影響因素。在后續的雙索懸掛系統理論研究中,若將這些結構參數無量綱化,則有望提出一些可行的設計準則。 1) 系統各剛體模態頻率與繩索預緊力呈正相關關系;3個轉動模態固有頻率中,滾轉模態的固有頻率最高且受影響最大,俯仰模態的最低且受影響較小;平動模態的固有頻率受繩索預緊力影響較小,升沉模態的固有頻率稍大于側滑模態的。 2) 雙索懸掛系統剛體模態頻率的高低與其系統總剛度直接相關,總剛度大的自由度方向剛體模態頻率也高,反之亦然。這一結果證明本文的研究方法是正確的。 3) 機身滑輪位置變化導致的繩系結構不同對滾轉模態固有頻率幾乎沒有影響,滑輪位置關于模型質心對稱時,繩系結構的變化對俯仰模態、偏航模態的固有頻率也幾乎沒有影響,但是滑輪位置關于模型質心不對稱時,對俯仰模態、偏航模態的固有頻率有不同程度的影響。 4) 雙索懸掛系統能夠在一定范圍內釋放模型除來流方向以外的5個自由度,且能使系統剛體模態頻率足夠低。 本文從理論和試驗兩方面驗證了繩系結構和繩索預緊力對全模顫振雙索懸掛系統剛體模態頻率存在影響,可以通過改變繩系結構和繩索預緊力來調整系統剛體模態頻率;所得結論可為雙索懸掛系統的理論研究及其結構的優化設計提供參考。2 雙索懸掛系統剛體模態
2.1 雙索懸掛系統地面樣機



2.2 系統靜剛度


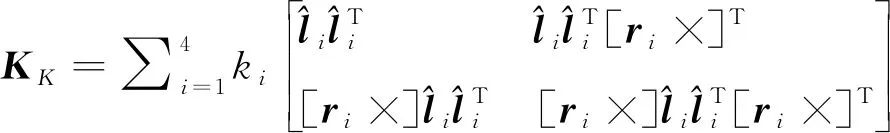


2.3 系統剛體模態頻率理論分析




3 系統剛體模態頻率測試
3.1 測試方法

3.2 測試結果



3.3 仿真與試驗結果對比

3.4 機身滑輪安裝參數的影響


4 結 論

