基于全局線性穩定性分析的翼尖雙渦不穩定特征演化機理

程澤鵬，邱思逸，向陽,*，邵純，張淼，劉洪

1. 上海交通大學 航空航天學院，上海 200240 2. 中國商用飛機有限責任公司 上海飛機設計研究院，上海 201210

翼尖渦是由機翼上下表面壓力差所產生，從機翼表面脫落后在飛機尾跡中形成的主要大尺度渦結構。翼尖渦的產生不可避免地帶來尾跡遭遇[1]、誘導阻力[2]和氣動噪聲[3]等問題，對飛機的安全性、經濟性和舒適性帶來不利影響。為此，國際民航組織(ICAO)對兩架飛機的起飛時間間隔和距離間隔做出嚴格的限定。以起飛重量超過136 000 kg的重型飛機為例，當后續飛機的起飛重量小于7 000 kg時，兩者的間隔時間不得少于159 s，間隔距離不得低于6海里[2]。除此之外，飛機在巡航過程中，由翼尖渦導致的誘導阻力占比達到30%～40%[4]。為減輕翼尖渦的不利影響，2002年，Gerz等從翼尖渦本身物理特征出發總結出兩大策略：① 降低翼尖渦的強度；② 加快翼尖渦的衰減[2]。在此基礎上，James和Frank于2018年從翼尖渦不穩定特性的角度進一步將其總結為：① 通過改變展向載荷或通過自然激發的不穩定性實現渦/渦系的修正和衰減; ② 通過使用某種形式的主動控制來施加外部擾動加速翼尖渦的失穩衰減[5]。翼梢小翼作為一種有效的減阻手段，已經成為大型客機不可缺少的一部分。翼梢小翼不僅降低翼尖渦強度，同時改變翼尖渦結構，進而影響翼尖渦的不穩定性特征；但是針對小翼結構下的翼尖多渦系統的不穩定性特征及其演化機理認識十分有限，限制了對于小翼的進一步改進和優化。如何使得小翼不僅能減阻，而且能控制翼尖渦穩定性使其快速衰減失穩值得深入研究。

翼尖渦的不穩定特性主要表現為長波不穩定性、橢圓不穩定性和翼尖渦的搖擺現象，對于其各自的演化機理一直以來都是研究的重點和熱點。翼尖渦的長波不穩定首先由Crow在分析等強度對轉Rankin渦對的流動現象中發現并闡述[6]，主要由以下3種效應共同疊加導致：① 與渦核流體旋轉方向相反的自誘導旋轉；② 由另一個渦引起的拉伸作用；③ 兩個渦的互誘導運動[7]。Leweke和Charles[8]的實驗結果和Grégoire等[9]的數值結果進一步表明，長波不穩定性表現為渦對關于其中心平面對稱的一種正弦變形，并與對稱面呈45°傾斜，變形幅度會沿流向逐漸增大直到兩個渦核最終接觸并重疊；隨后翼尖渦發生重新連接，在經歷若干個周期后，最初的渦對轉變成一系列三維渦環。短波不穩定性則源自于渦對中一個翼尖渦的兩個擾動波(開爾文模態)與另一個渦對產生的應變場之間的共振機制，這種共振可以導致擾動波按照指數規律放大，從而引起渦旋的不穩定性。在較低的雷諾數(103～105)條件下，發生開爾文模態的共振條件為兩個開爾文模態周向波數之差為2，Leweke和Charles[10]對無軸向流動的渦對運動分析結果表明，共振條件是擾動模態的周向波數為-1和1的組合；Roy等[11]驗證了有軸向流動的渦對運動中，共振條件是擾動模態的周向波數為2和0的組合。而在更高雷諾數條件下，共振條件則要求兩個開爾文模態周向波數之差為3[7]，并且在渦最終破碎耗散之前還會引起二次不穩定[12]和渦的重連[13]等更為復雜流動現象。翼尖渦的搖擺現象首先由Baker等在水槽實驗中發現[14]。隨后，Devenport等[15]的熱線實驗結果也證實翼尖渦搖擺現象的存在，分析結果表明翼尖渦搖擺幅值隨流向位置而逐漸放大。Edstrand等[16]對體視粒子圖像測速(SPIV)結果分析，發現由線性穩定性分析(LSA)獲得的最不穩定模態結構與由本征正交分解(POD)獲得的主模態結構一致，從而科學地說明翼尖渦搖擺運動來源于不穩定性。在此基礎上，本文作者團隊[17-18]研究表明在低湍流度情況下，搖擺幅值隨不同工況(雷諾數、攻角)和流向位置的發展規律與由局部線性穩定性分析獲得的不穩定放大因子(頻率、波數)隨不同工況和流向位置的變化規律具有一致性，從而更進一步地揭示翼尖渦搖擺現象的來源。

對翼尖渦的不穩定模態及其演化機理的研究有助于理解翼尖渦不穩定現象背后的物理本質，對于翼尖渦的科學控制原理有指導意義。相對于局部 LSA只能對近似軸對稱的孤立翼尖渦進行線性穩定性分析, 全局線性穩定性分析(Bi-global LSA)能對雙渦及雙渦以上、渦與尾跡的相互作用等復雜流動現象予以分析。Moored等[19]對槳葉施加與用Bi-global LSA得到卡門渦街的最大空間生長率相對應的驅動頻率時，獲得最優的推進效率。當卡門渦街的不穩定模態發生轉捩時，對應的尾跡結構會從一種結構變成另一種結構形式[20]。這些結果對基于翼尖渦不穩定模態的控制思路具有很好的啟發意義。此外，理論分析表明，孤立Lamb-Oseen渦[21]/渦對[22]、Batchelor渦[23]均對周圍環境存在一個最不穩定的擾動。在最不穩定擾動的作用下，孤立渦獲得的擾動增益可達到102～103；渦對獲得的擾動增益可達到104。在準定常演化階段，以觀察者的視角和渦的視角，擾動能量均會逐漸增強；此外，雷諾數越大，翼尖渦不穩定模態的擾動能量也會增加[21,24]。然而，這些研究都是理論渦模型，較難真實反映實際翼尖渦的流動不穩定性。最近，Edstrand等[25]在Re=1 000下，針對NACA0012等直機翼產生的翼尖渦及其尾跡進行時間和空間的全局穩定性分析，結果表明帶尾跡的孤立渦特征值在時間和空間上存在尾跡分支、渦主分支和連續分支；在空間上還包含渦次級分支。尾跡分支則主導流動中最主要的不穩定特性。進一步地，按照尾跡分支中的不穩定頻率施加外部擾動時，發現按照第五階模態施加的體積力會使翼尖渦獲得最優的衰減[26]，從而提供低雷諾數下孤立翼尖渦的不穩定控制解決方案。然而，較高雷諾數下翼尖雙渦系統的不穩定模態和演化機理的研究，仍然是一個新的課題。

為此，本文采用SPIV方法對加裝雙叉彎刀小翼的M6機翼在不同攻角、不同雷諾數，16倍尾跡區范圍內的翼尖渦流場展開測量。采用Bi-global LSA來分析求解翼尖雙渦結構的不穩定放大率和模態，在此基礎上得到雙翼尖渦結構在不同擾動波數和不同工況下的不穩定模態的演化機理，從而為加快翼尖渦的失穩衰減科學原理探討和提出工程解決方案并提供參考。

1 試驗搭建與數據處理

1.1 試驗模型

試驗中使用的模型為加裝雙叉彎刀小翼的M6機翼。如圖1所示，后掠機翼翼根弦長為0.143 m，根梢比為0.56，展弦比為3.8，其他參數參照M6機翼。上、下小翼參照Whitcomb小翼構型設計，兩者傾斜角均為60°，前緣后掠角分別為38°、52°。后掠翼和小翼連接處均保持光滑連接，以避免拐角處產生不必要的渦結構。

圖1 機翼模型外形幾何參數Fig.1 Geometric parameters of examined model

1.2 SPIV測量

本試驗在上海交通大學低速回流式風洞中進行,該風洞的試驗段截面為1.2 m×0.9 m的矩形，經過熱線標定測得來流湍流度在0.3%以下。試驗時，機翼安裝攻角α為6°、8°和10°；來流速度u∞為15 m/s、30 m/s和45 m/s，對應的基于翼尖弦長(c=0.08 m)的雷諾數為Rec=0.82×105，1.64×105,2.46×105。相對于后掠翼的尾緣，在16倍尾跡區范圍內等距離測量x/c=2，4，…，16共8個截面。試驗過程中機翼的安裝示意圖如圖2 所示，其中來流方向為x軸正方向，機翼上表面方向為y軸正方向，垂直于風洞壁面向上的方向為z軸正方向。由機翼和小翼造成的風洞阻塞度小于1%。

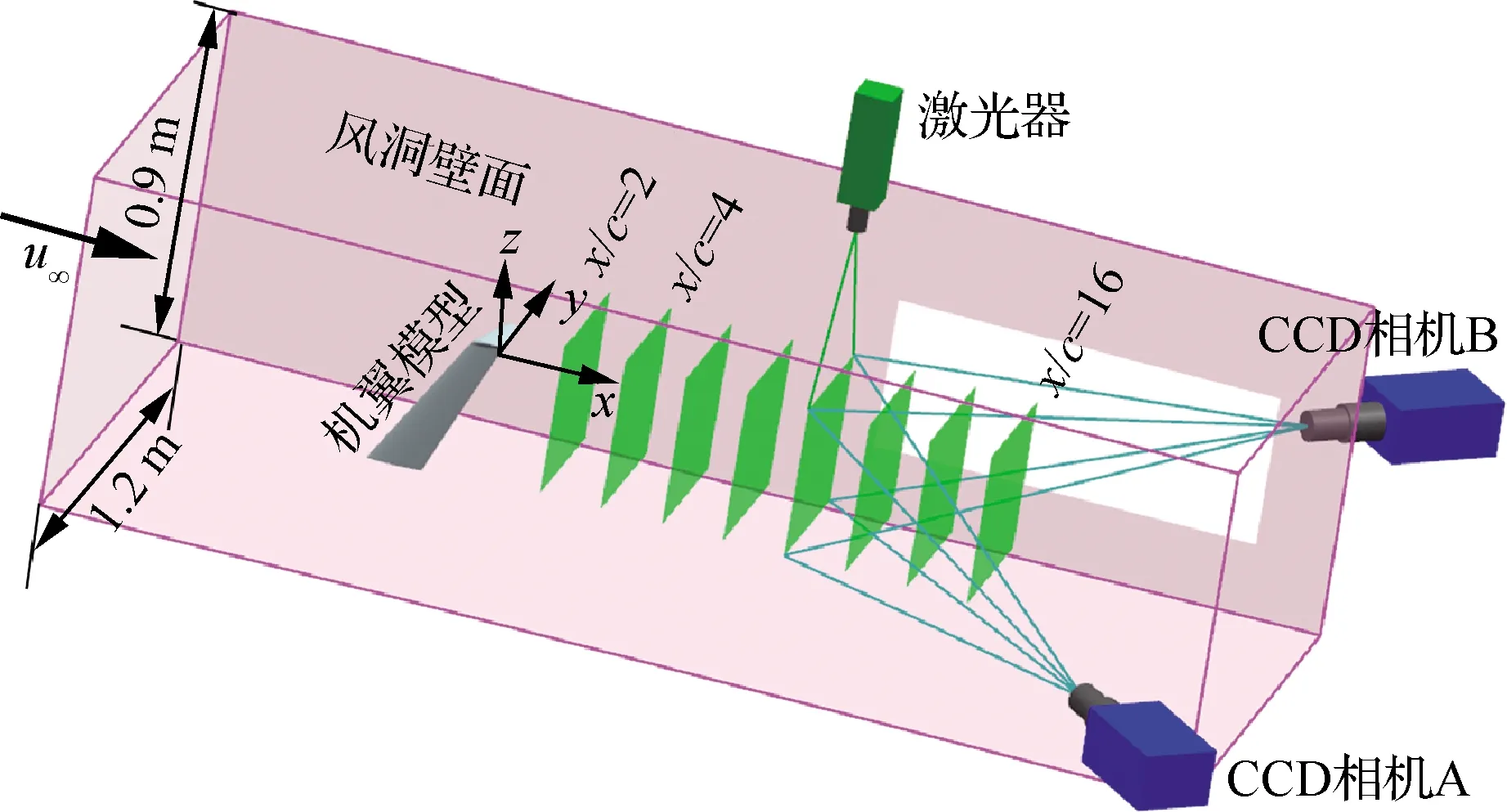
圖2 SPIV試驗示意圖Fig.2 Schematic diagram of SPIV test

試驗過程中，示蹤粒子采用1～5 μm直徑的霧化乙二醇油滴，保證良好的粒子跟隨性。采用Nd:YAG雙脈沖激光發射器發射波長為532 nm、脈沖能量為380 mJ的激光照亮測量區域。雙脈沖發射頻率為1 Hz，激光厚度為1 mm并垂直于來流方向。根據SPIV的測量精度對粒子在兩幀圖像時間內的位移要求，在15 m/s、30 m/s和45 m/s的來流條件下，兩束激光的時間間隔分別設為Δt=15，7.5，5μs。試驗拍攝的相機為Imager-Pco的高分辨率CCD相機，相機與激光器同步，發射與采樣周期設置為1 s。為保證相機在x/c=16截面處的拍攝窗口足夠，兩個相機的安裝角度保持在45°。相機采集的圖像畫幅為2 048像素×2 048 像素，拍攝畫幅大小為292 mm×269 mm，對應的空間分辨率為0.131 mm/像素。每個工況下，左右相機均保存200幅瞬時圖像，以求解時均流場信息并研究翼尖渦的搖擺特征。

采用TSI INSIGHT 4G軟件對圖像進行互相關計算。通過兩次查詢窗口確定粒子位移以提高速度矢量分辨率，初始查詢窗口為72像素×72像素，有效重疊率為25%；第2次查詢窗口為36像素×36像素，有效重疊率為50%，并通過9像素×9像素的填充算法由周圍矢量插值出未能解算的速度矢量，后處理得到的達標矢量占總矢量的85%以上。由此產生的整個測量平面區域速度的測量誤差小于1%[17]，滿足試驗結果的分析要求。

1.3 翼尖渦相關物理量的計算

在試驗后處理中，瞬時流場和時均流場中翼尖渦的渦核位置均采用渦量質心公式的方法確定。以瞬時流場的計算為例，渦心位置(yc(t),zc(t))的計算式為

(1)

式中：ωx(y,z,t)為瞬時渦量；為去除試驗中噪點對結果的影響，考慮置信范圍，積分區域S1為集中最大渦量絕對值95%以上的渦量區域，即

|ωx(y,z,t)|≥0.05|ωx(y,z,t)|max

(2)

時均流場中的渦核半徑采用與渦心位置類似的方式確定：

(3)

式中：yc、zc為時均流場中的渦心坐標；ωx(y,z)為時均流場中的流向渦量；積分區域S2的定義與S1類似。

2 全局線性穩定性分析方法

2.1 擾動方程

本試驗中產生翼尖雙渦結構，流場已不滿足軸對稱條件，但是在流向方向上可認為近似滿足準平行流假設。此時，需采用Bi-global LSA對翼尖雙渦結構展開穩定性分析。采用圖2笛卡爾坐標系(x,y,z)下的不可壓縮Navier-Stokes方程，流場中速度和壓力等流動變量可表示為

(4)

忽略流向變化，基于傅里葉分解思想以線性小擾動表示的脈動矢量可寫為

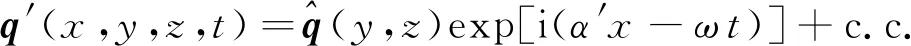
(5)

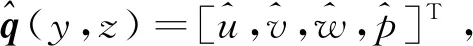
將流場變量代入不可壓Navier-Stokes方程中，消去定常流動方程并略去高階小量，得到Bi-global LSA的小擾動控制方程為

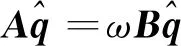
(6)

式中：A、B為穩定性矩陣，分別為

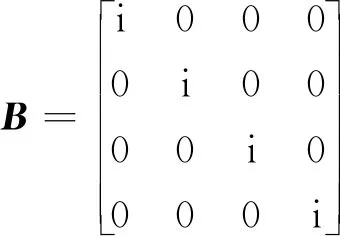
(7)

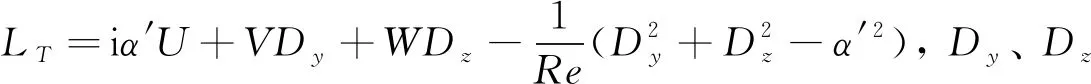
考慮到數值精度和收斂速度的要求，方程(6)的離散采用切比雪夫譜配置法[17，26]，對應的邊界條件信息可參見文獻[17]。通過求解方程(6)可得到特征值譜(ωr,ωi)和對應的特征向量。特征值中，ωi為翼尖渦流動在時間上最不穩定擾動模態對應的放大率。按照式(5)的結果可知，當ωi>0時，擾動在時間上會以指數形式衰減，即流動是不穩定的,而特征向量即為所期望得到的擾動模態信息。

2.2 程序驗證

在對本文的翼尖雙渦流場展開Bi-global LSA之前，先采用槽道流、孤立翼尖渦、等強度對轉渦對、等強度同轉渦對4個典型算例對程序予以嚴格的驗證。在驗證過程中，與文獻結果保持一致，切比雪夫譜配置點的數目均為64×64。

在槽道流動驗證計算中，設置條件與Theofilis等[27]的算例一致，寬高比分別為A=1，4。圖3 為兩者特征值譜的比較結果,可以發現，對于兩種寬高比，特征值譜均符合完好。

圖4(a)和圖4(b)分別為孤立Batchelor渦和對轉渦對[28]的全局時間穩定性驗證結果，其中Batchelor渦的旋擰度q=0.475,Re=100，方位波數m=-1，流向波數α′=0.418。可以看出，無論是孤立渦，還是對轉渦對，兩種方法所得到的特征值譜基本吻合。特別地，對于ωi>0半平面上的不穩定特征值可以實現精準捕捉。

圖3 槽道流結果驗證Fig.3 Validation of cavity flow results

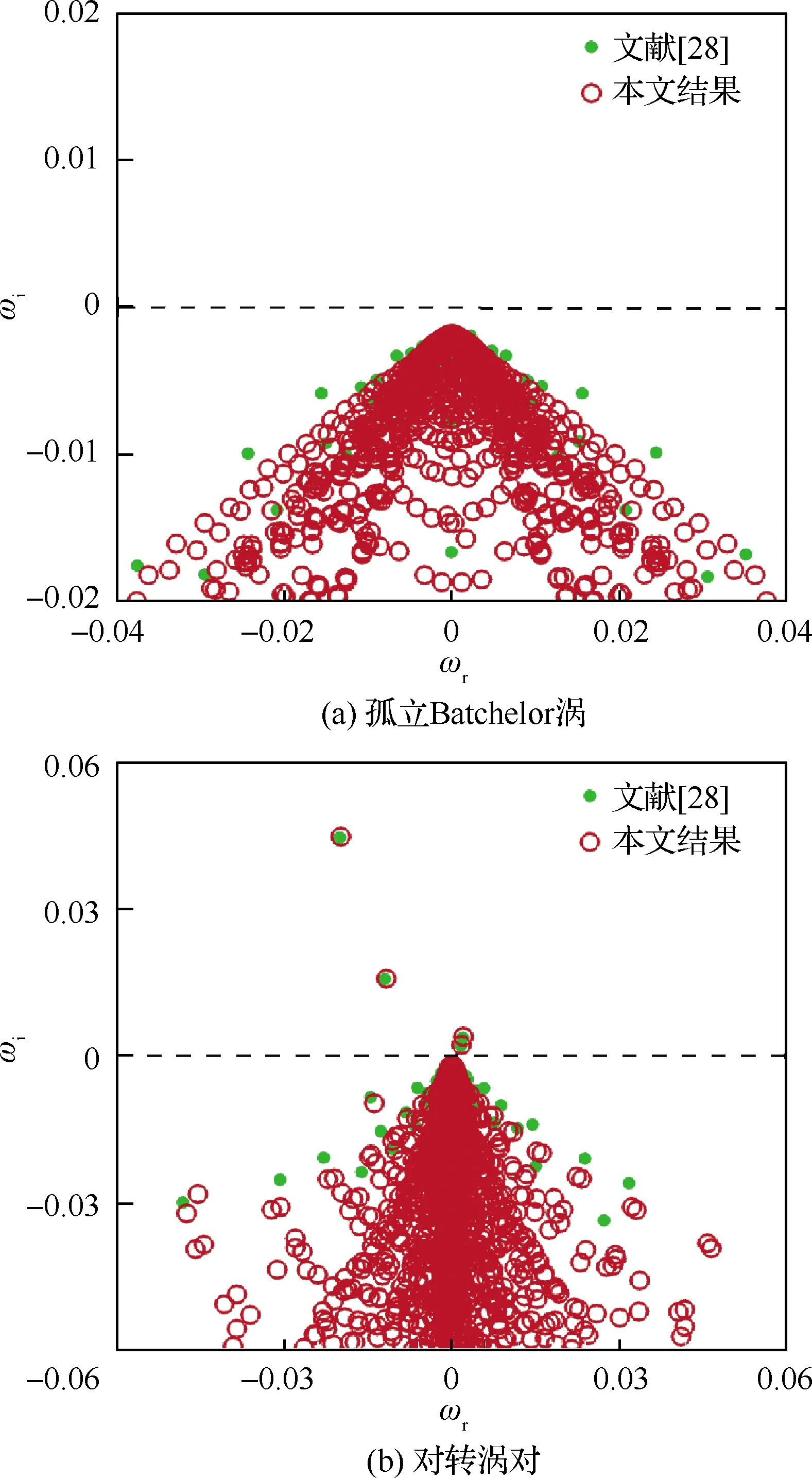
圖4 孤立Batchelor渦和對轉渦對的結果驗證Fig.4 Validation of isolated Batchelor vortex and counter rotating vortex pairs results

在類似的參數條件下，Mayer和Powell[29]也曾做過孤立Batchelor的計算，表1列出本研究中得到的最不穩定特征值與Mayer和Powell的結果。可以看出，本研究計算得到的最不穩定特征值與文獻[29]保持一致。

表1 孤立Batchelor渦流的結果驗證Table 1 Validation of isolated Batchelor vortex flow results

為驗證程序獲取的擾動模態的準確性，程序還選取同轉渦對作為驗證算例。計算時初始流場為兩個線性疊加的高斯渦，其初始渦核半徑均為a=0.010 408 m, 渦心間距b=0.074 336 m，兩渦的環量Γ1=Γ2=0.204 5 m2/s。

由于線性疊加的渦對并不是Navier-Stokes方程的解，以此為初始條件做無黏計算，在經過一個快速的松弛過程后，選取此時的流場作為全局時間穩定性分析的基準流動。此時a=0.011 2 m,Γ1=Γ2=0.204 3 m2/s，b=0.074 06 m，由此得到基于環量的雷諾數Re=13 989,a/b=0.15，流向速度為0 m/s。計算時流向波數與Roy等[11]的設置保持一致，取α′=2.0。在得到的特征譜中選取不穩定點，可以求解得到擾動模態，其結果與Roy等的結果對比如圖5所示,可以發現，本程序對同轉渦對中的擾動模態可以實現準確的捕獲。

以上計算結果表明本文采用的方法對不穩定特征值譜和擾動模態均可以進行精確的捕捉，能夠滿足試驗中得到的翼尖雙渦結構流場的全局穩定性分析要求。

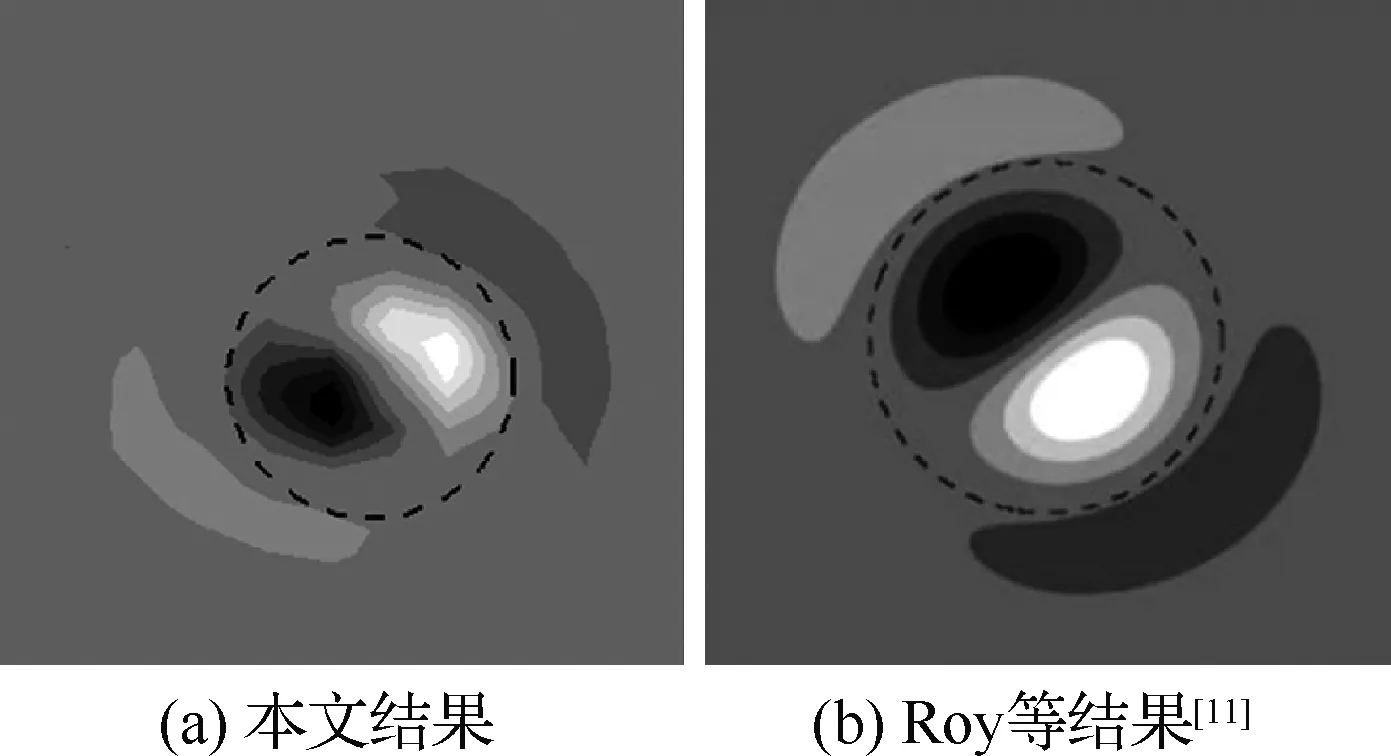
圖5 同轉渦對的擾動模態結果驗證Fig.5 Validation of co-rotating vortex pairs flow results

2.3 翼尖雙渦結構的Bi-global LSA 方法

進行全局線性穩定性分析時，關鍵之一是基本解的獲取。在基于SPIV得到時均流場后，獲取基本解之前還需進行以下步驟：① 對分析截面上的每個翼尖渦周向平均，獲取旋向速度；② 對翼尖渦采用Lamb-Oseen渦模型擬合，并線性疊加；③ 在數值計算平臺上對線性疊加渦對松弛計算[11,30-31]，使其滿足Navier-Stokes方程的解；④ 以 流向渦量重構出軸向速度[11, 32]，從而獲得最終的基本解。

本研究中，為盡可能消除尾跡對渦不穩定性潛在的影響，選取x/c=16截面處的時均流場作為分析截面。此外，根據已有結果，該風洞品質下，渦搖擺對速度場的影響十分有限[17]，因此分析流場沒有考慮渦核對齊后的平均流場。松弛處理過程在商業軟件Fluent中進行，具體表述為：采用Fluent中的用戶自定義函數將線性疊加渦對作為初始條件，在1.28 m×1.28 m的正方形區域內對計算域初始化，網格規模為1 600×1 600。區域邊界設置為速度入口條件，由于本次計算只是純粹的松弛耦合過程，不考慮外部速度輸入，所以速度項設置為0，而壓力和溫度條件則與風洞試驗所記錄的數據保持一致。流場求解采用無黏、非定常、基于壓力的SIMPLE算法。計算總時間步數為300步，時間步長設置為0.000 1 s, 每個時間步的內迭代次數為20次，空間離散采用二階迎風格式，時間推進采用二階隱式格式。初始化完成后，計算域和初始流場如圖6 所示,v、w是瞬態速度。

松弛計算后的流場缺少軸向速度信息，為此，采用Roy等[11, 32]對等強度同轉及對轉渦對的方法，獲得流向速度為

圖6 計算域和初始化后的流場Fig.6 Computation domain and flow field after initialization

(8)

式中：δ表示基于Lamb-Oseen渦的翼尖渦渦核半徑；δG為試驗測量流向速度的高斯分布特征半徑；U(0,0)及ωx(0,0)為渦心處的速度和渦量。

圖7為SPIV試驗得到的軸向速度減少量和流向渦量與CFD計算結果，下標d和u分別代表下主渦和上主渦。可以看出，相關特征物理量符合完好。

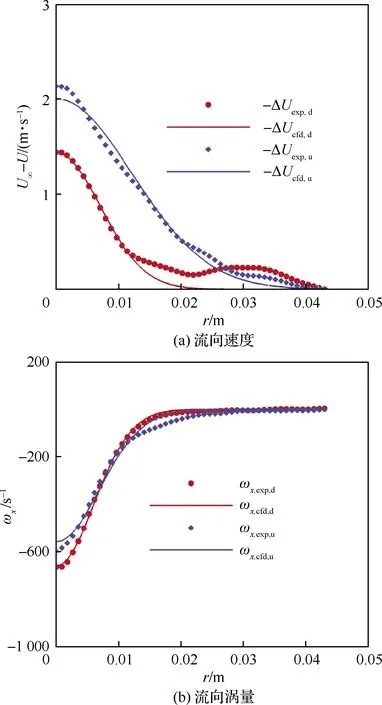
圖7 SPIV試驗與CFD結果比較Fig.7 Comparison of SPIV test and CFD results

基準流動是用切比雪夫譜配置點的方法將其映射到計算域內。為此，涉及到配置點數目對特征值譜的影響問題。為確定配置點數目，以α=6°、Rec=1.64×105產生的翼尖渦流場為例，分別用48×48、64×64、80×80這3套網格在擾動波數α′=1.25下進行全局穩定性分析計算，其結果如圖8所示。可以發現，不同配置點數下所得到的特征值譜在穩定半平面內的樹狀連續分支位置基本不變，只是不穩定平面內離散點位置有所差別。對不穩定半平面中隨譜配置點數變化的動點分析表明，其所對應的擾動模態為數值離散產生的計算誤差，點本身為數值偽點；而不動點及其特征向量則表征具有物理意義的擾動模態。由此確定特征值譜中的兩個主要模態：模態P和模態S，它們在3套網格下的特征值如表2所示。結果表明，以64×64作為計算網格能夠滿足分析要求。在接下來的計算中，為更明確區分開動點和不動點，所有計算和分析結果均基于56×56、64×64兩套網格的結果進行。

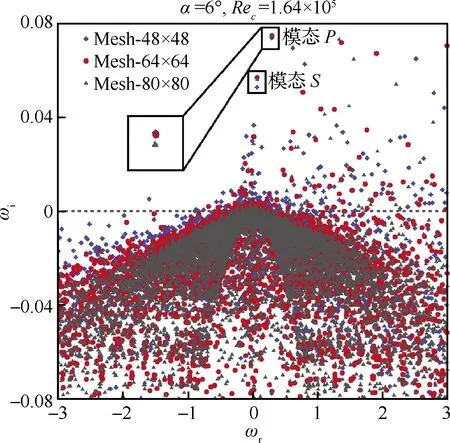
圖8 配置點數無關性驗證(α′=1.25)Fig.8 Validation of mesh independence (α′=1.25)

表2 不同配置點數下模態P和模態S對應的特征值對比

3 翼尖雙渦結構及其不穩定性特征

3.1 翼尖雙渦的結構形態

以α=8°、Rec=1.64×105為例，試驗得到的時均流場如圖9所示。結果表明，雙叉彎刀小翼的翼尖渦為由上小翼產生的上主渦和下小翼產生的下主渦所構成的同轉渦對形式。注意圖中視角上方的翼尖渦為下主渦，下方的翼尖渦為上主渦。由于本試驗的精心設計，該渦對近似為等強度，其中下主渦的環量為-0.299 7 m2/s，上主渦的環量為-0.321 4 m2/s；渦心坐標位置分別為(-0.003 222 m, 0.107 2 m)、(0.045 46 m, 0.049 26 m)。

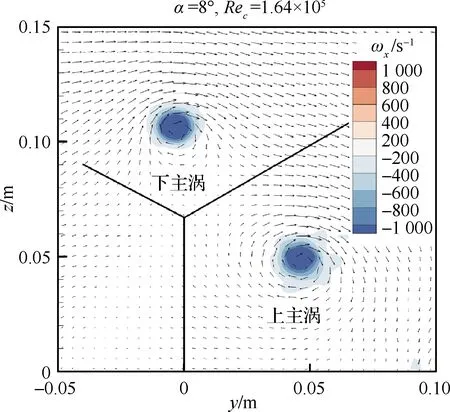
圖9 試驗得到的翼尖雙渦時均流場云圖Fig.9 Time averaged flow field contour of vortex pair from experiment

3.2 翼尖渦的不穩定特征：翼尖渦的搖擺

圖10為試驗中產生的同轉渦對的搖擺現象，其中藍色實線區域和黑色虛線區域分別表征翼尖渦搖擺幅值和渦核半徑的圓形區域，可以看出，翼尖渦的搖擺區域始終在渦核半徑范圍之內。

x/c=4，10，16下，下主渦的時均渦核位置分別為(-0.018 72 m, 0.094 15 m)、(-0.006 937 m, 0.102 m)、(-0.003 222 m, 0.107 2 m)；上主渦的時均渦核位置分別為(0.081 67 m, 0.082 74 m)、(0.067 91 m, 0.057 41 m)、(0.045 46 m, 0.049 26 m)。可以發現，隨著翼尖渦向遠場演化，下主渦逐漸向y+、z+方向移動；上主渦逐漸向y-、z-方向移動，在這過程中，兩渦逐漸靠近的同時而相互纏繞[7]。從x/c=4到x/c=16，兩渦的距離從開始的0.101 m逐漸減小到0.075 68 m，而相對于y軸正方向的夾角θ則從6.48°增加到49.96°，由此可以得到該同轉渦對在整個過程中的平均旋轉角速度為20 rad/s。

對不同攻角、不同雷諾數下的翼尖渦搖擺幅值以對應的渦核半徑無量綱化(σ/γc)，可以得到如圖11所示的不同工況下的無量綱搖擺幅值隨流向位置的變化規律。從圖中可以看出，無量綱搖擺幅值隨流向位置在逐漸增加；而上主渦的搖擺幅值總體來說均要大于下主渦的搖擺幅值，表明上主渦可能是一種更不穩定的狀態。進一步地，可以發現不同工況上主渦的搖擺幅值對雷諾數和攻角變化更敏感。與NACA0015等直翼的孤立翼尖渦的搖擺幅值變化規律類似[17-18]，隨著雷諾數增加，搖擺幅值也逐漸放大。然而隨著攻角的變化，搖擺幅值的變化不是單調的，在α=8°下搖擺幅值最大，這可能與翼尖渦的不穩定放大率有關(詳見3.3節中的討論)。

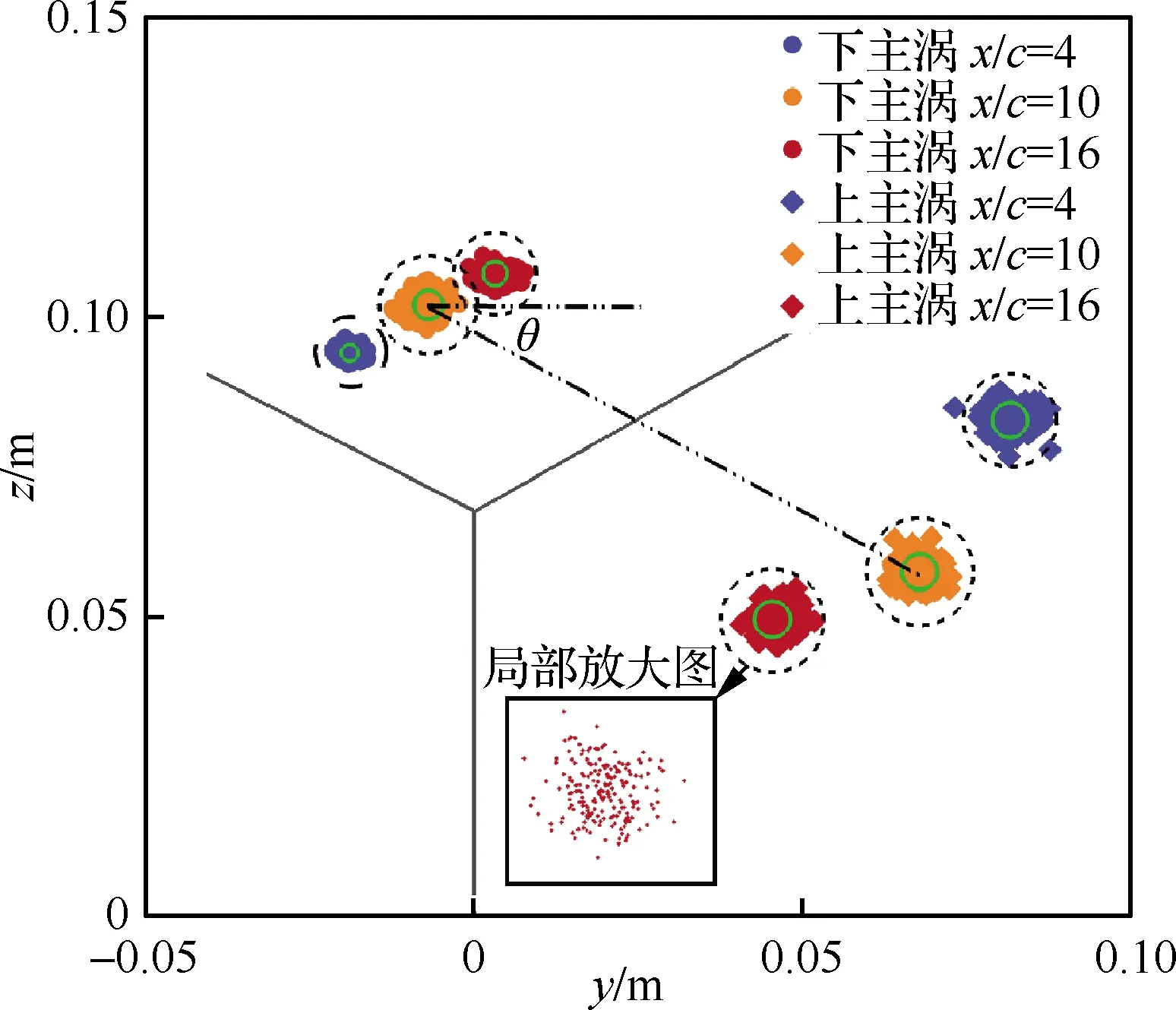
圖10 翼尖雙渦結構的渦核搖擺Fig.10 Vortex wandering of wingtip vortices

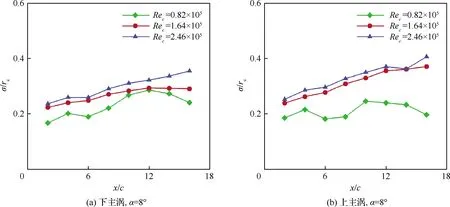
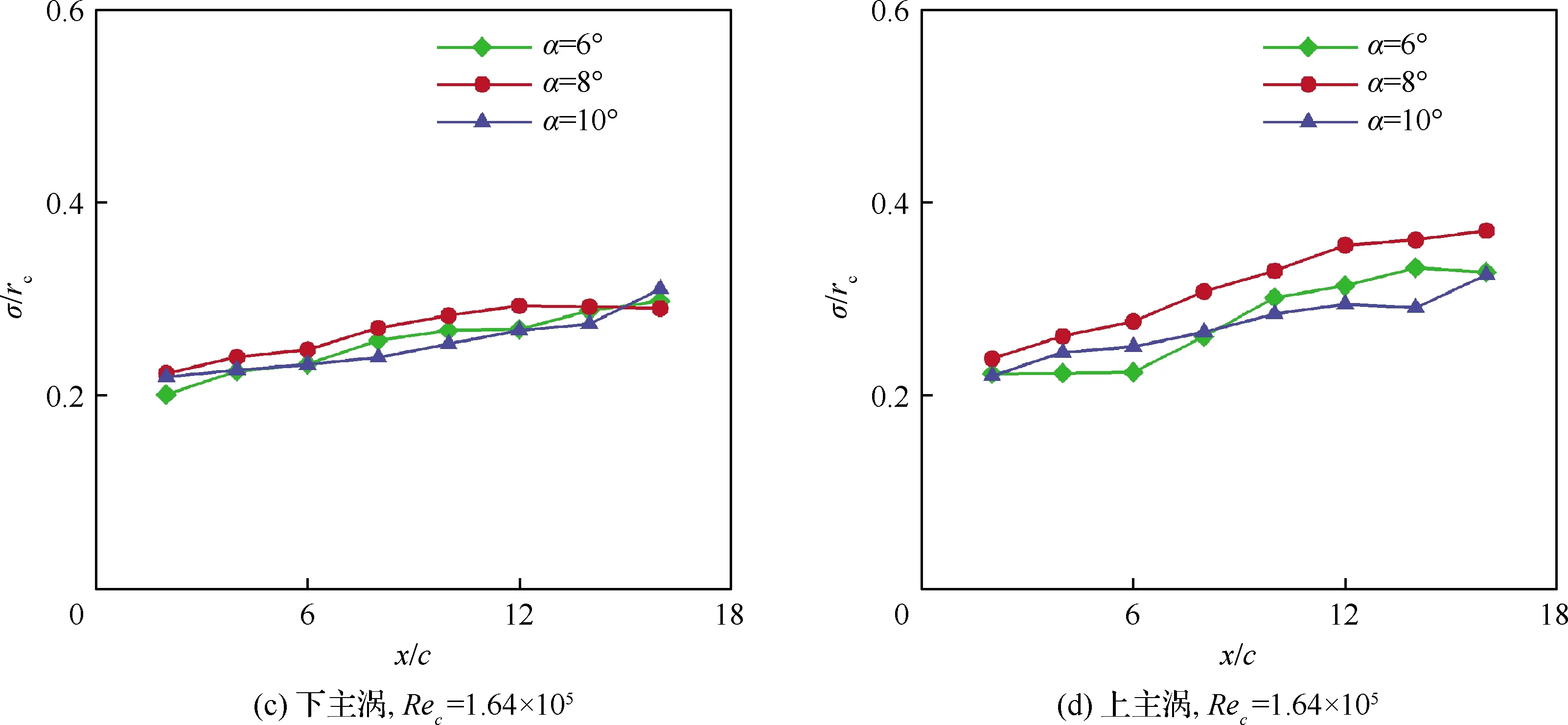
圖11 不同工況下翼尖渦搖擺幅值隨流向位置的變化Fig.11 Wandering amplitudes as functions of streamwise locations of wingtip vortex under different flow conditions

3.3 翼尖渦的不穩定特征：穩定性曲線

對于每一個工況而言，通過掃描不同擾動波數的特征值譜，可以得到對應的不穩定放大率，由此得到如圖12所示的穩定性曲線。從圖中可以發現，在各工況下，試驗產生的翼尖渦的時間不穩定性放大率均大于0，這意味著翼尖渦是時間不穩定的，即擾動將隨時間不斷放大，超過一定閾值后擾動將使翼尖渦進入非線性發展階段。此外，左右兩列的對比結果表明，上主渦最不穩定模態(模態P)的不穩定性放大率均大于下主渦最不穩定模態(模態S)，這證明模態P在該流動中占主導地位，即上主渦的不穩定性顯著強于下主渦，其擾動將隨時間更快地發展而導致翼尖渦的衰減失穩。進一步分析流動條件對該雙渦結構不穩定性的影響，可以發現模態P受雷諾數與攻角變化影響很大，而模態S則基本維持不變。在與圖11中的結果相互印證時，也表明上主渦相對于下主渦更易于受到外界擾動的影響，是一種潛在的可調控模態。

此外，由穩定性曲線可以得到上主渦與下主渦最不穩定擾動的流向波數α′。在Rec=0.82×105～2.46×105、α=6°～10°范圍內，翼尖渦最不穩定模態的擾動流向波數均分布在α′=[2.75,5]的區間內。在SPIV試驗基礎上經過N-S方程松弛結果得到的基于環量的特征速度Uc≈5 m/s，渦核半徑δ≈0.01 m，由此可得有量綱的翼尖渦最不穩定擾動流向波數約為α*=1 800 rad/m，即沿流向每米包含約30個周期的擾動，擾動流向波長λ≈0.03 m，與翼尖渦渦核半徑rc≈0.01 m可比。因此，本研究中雙叉彎刀小翼產生的同轉渦對所呈現的是一種短波不穩定性。

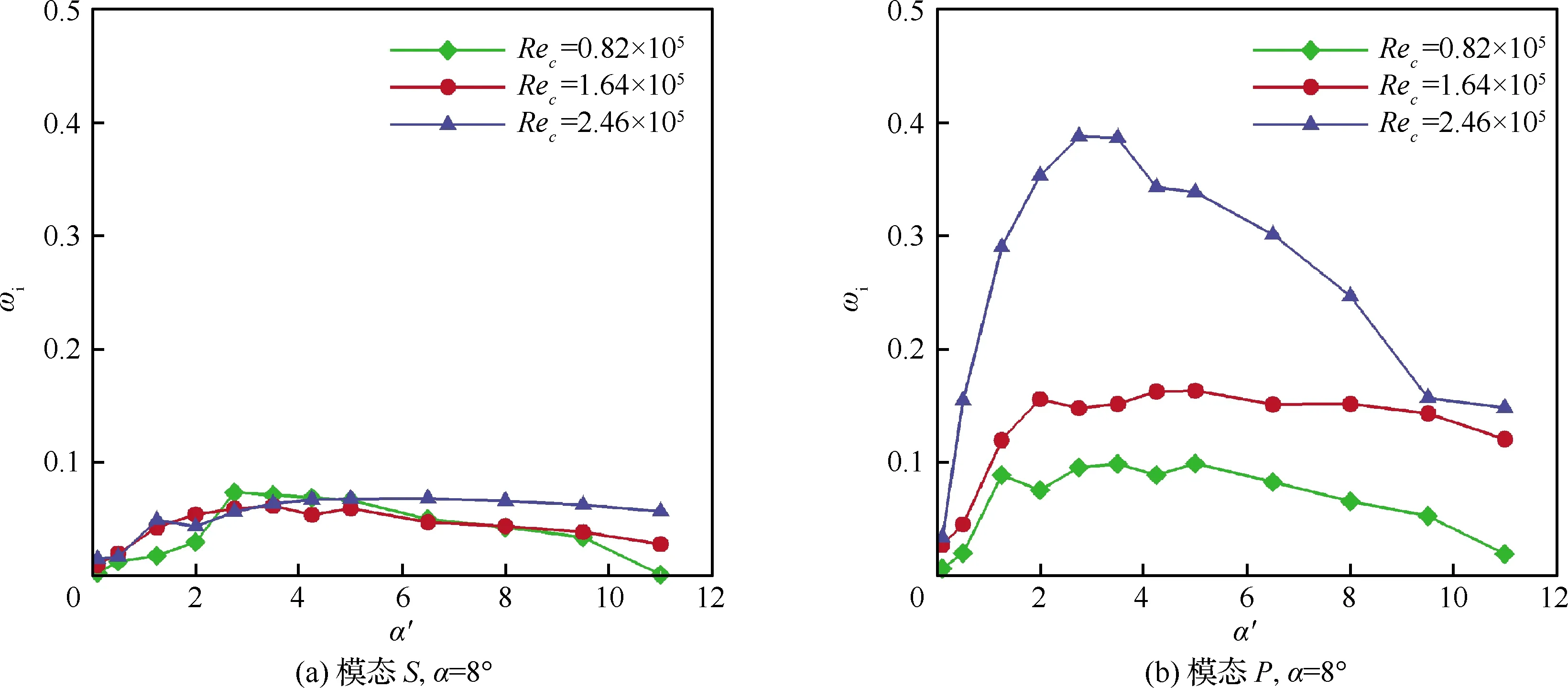
圖12 各工況下翼尖渦的穩定性曲線Fig.12 Stability curves of wingtip vortex under different flow conditions

4 翼尖渦的不穩定模態演化機理

4.1 不同擾動波數下翼尖渦最不穩定模態

以α=8°、Rec=0.82×105工況為例，研究分析不同擾動波數α′下的下主渦最不穩定模態(模態P，圖13)和上主渦最不穩定模態(模態S，圖14)的演化行為。為顯示更清晰，模態P前兩個子圖的無量綱顯示范圍分別為[-0.05,0.05]、[-0.15,0.15]，其他子圖的顯示范圍為[-0.2,0.2]；而模態S的子圖保證相同的顯示范圍，均保持在[-0.05,0.05]區間。

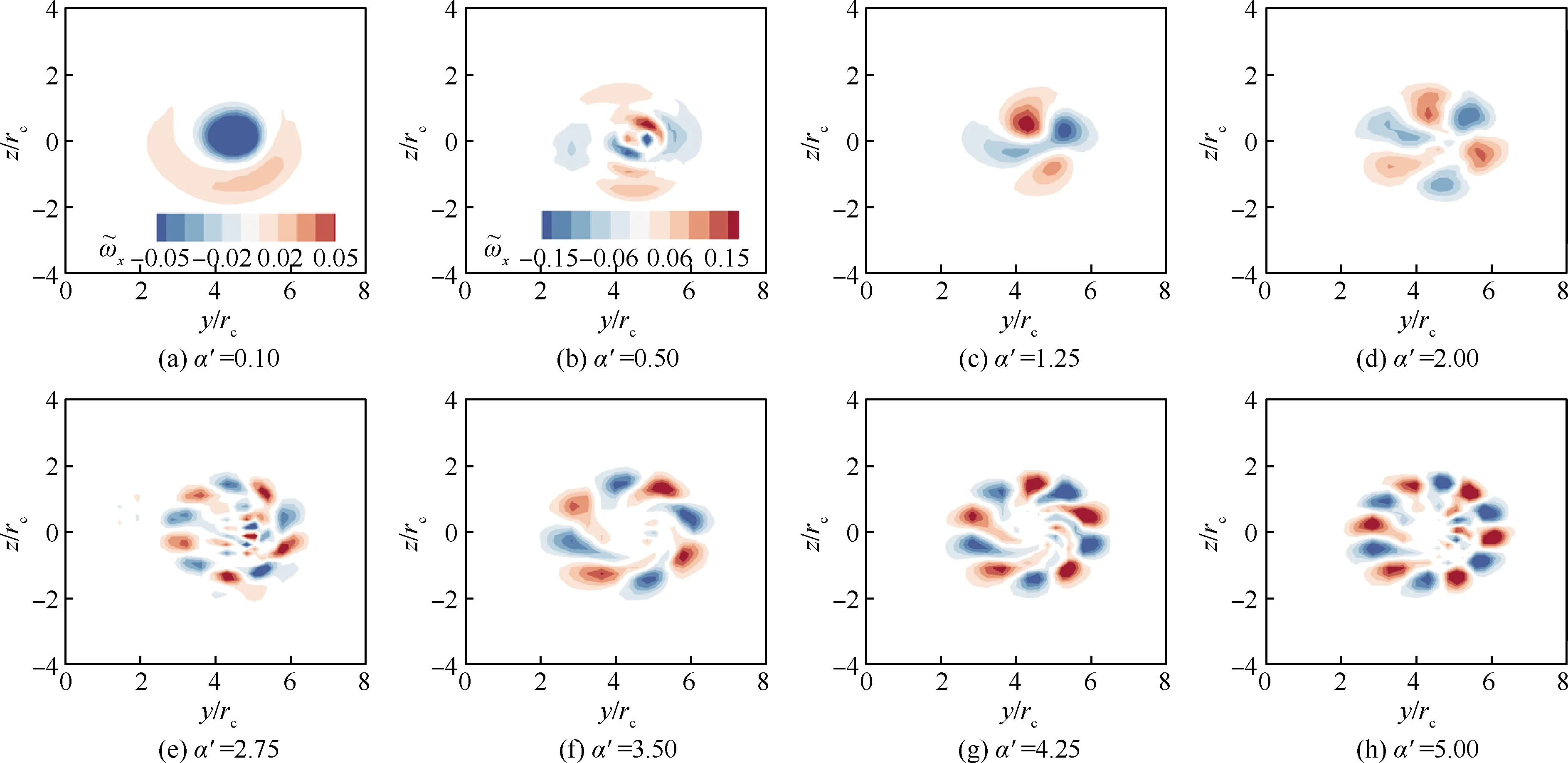
圖13 不同擾動波數下模態P的演化Fig.13 Evolution of perturbation Mode P under different wavenumbers

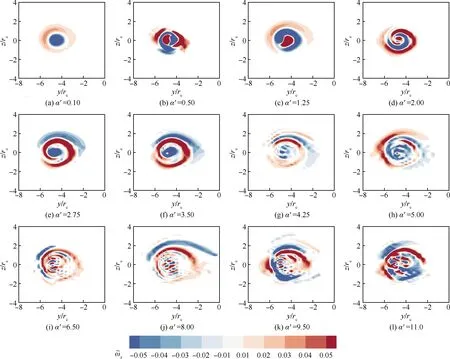
圖14 不同擾動波數下模態S的演化Fig.14 Evolution of perturbation Mode S under different wavenumbers

可以發現，盡管兩渦近似為等強度同轉渦對，但模態P和模態S在結構特征上隨著擾動波數的增加明顯不同。如圖13(a)和圖14(a)所示，當擾動波數α′=0.1時，此時幾乎沒有外部擾動，模態P和模態S的形態結構一致，均為軸對稱的模態，兩者只有徑向波數n=1，而切向波數m=0。但隨著擾動波數α′的增加，模態P的切向波數也隨之增大，在圖13(g)中，α′=4.25時切向波數增至m=5；而α′=9.5時，m=11；但在此過程中，徑向波數卻變為0。對于模態S而言，擾動波數的增加改變的是徑向波數n，而非切向波數。以圖14 (c)中α′=1.25為例，此時徑向波數n=2；當α′=5.0時，圖14(d)顯示的模態S徑向波數至少達到n≥3。當擾動波數α′進一步增大時，模態S的徑向波數已經超過64×64的切比雪夫譜配置點網格所能解析的范圍，但可以預計徑向波數會進一步增加。

需要指出的是，在獲取上/下主渦最不穩定的模態時，要特別注意兩個模態并存的耦合模態給模態識別上帶來的干擾。事實上，對于耦合模態來說，類似圖13和圖14子圖中的兩種模態會分別位于各自渦核的附近區域，同時，其模態能量比下主渦的最不穩定模態的能量要強，比上主渦最不穩定模態的能量要弱。然而耦合模態在翼尖渦的演化中的作用及其調控機理尚不清楚，可在后續的工作中進一步研究。

4.2 不同工況下翼尖渦最不穩定模態

圖15顯示雙叉彎刀式小翼翼尖渦的模態P和模態S在與基準流動相同的坐標系下的比較。圖中左邊為模態S，右邊為模態P，可以發現模態S均準確位于下主渦渦核處，而模態P則均落在上主渦的渦核處。在各工況下，上主渦模態的擾動強度均大于下主渦，進一步表明在雙叉彎刀式小翼的同轉渦對中，模態P對翼尖渦不穩定性起主導作用，且其最不穩定模態均為大切向波數的擾動，各工況的切向擾動波數均達到m=5～6。對于α=10°、Rec=1.64×105條件下的最不穩定擾動模態，可以發現模態P與模態S強度較為相近，其模態之間的相對強度也與圖12中穩定性曲線結果相符。

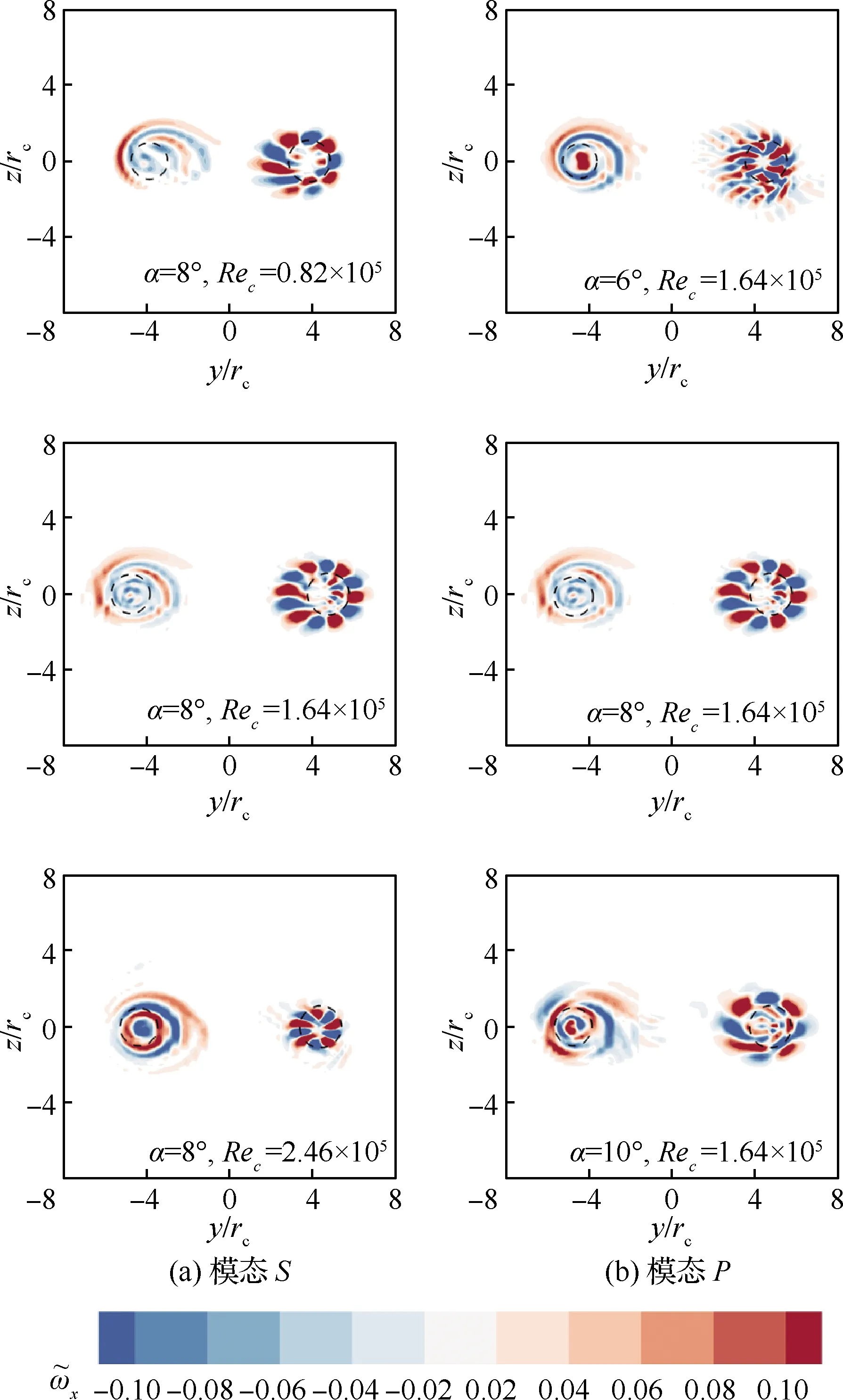
圖15 不同工況下翼尖渦對的最不穩定模態Fig.15 The most perturbation modes of wingtip vortex pair under different flow conditions

圖15中還標注不同工況下渦核半徑的相對大小，可以發現，主渦模態的螺旋狀、大切向波數擾動均緊貼渦核邊界，在各工況下均有部分擾動穿透渦核邊界進入渦核內部。特別地，對于α=8°、Rec=2.46×105工況，模態P擾動的絕大部分均已進入上主渦的渦核。在這種擾動模態的強作用下，該工況下的上主渦是所分析的所有工況中最不穩定的，這也與圖12中穩定性曲線結果相符。

5 結 論

通過SPIV試驗獲得不同攻角、不同雷諾數、x/c=16范圍內的雙叉彎刀小翼翼尖渦流場，在CFD中經歷簡單的松弛階段獲得基準流動，并在此基礎對其展開全局時間線性穩定性分析，得到以下結論：

1) 試驗中對稱布置的雙叉彎刀小翼產生的翼尖渦包含上/下小翼產生的主渦(上/下主渦)結構，兩者構成近似等強度的同轉渦對，兩者相互靠近的同時，以約20 rad/s的角速度相互纏繞。

2) 試驗產生的同轉渦對搖擺幅值隨流向位置逐漸增大，隨雷諾數的增加而增大，隨攻角的增加先增大后減小。不同工況下，上/下主渦最不穩定模態(模態P/模態S)的穩定性曲線的變化規律與搖擺幅值的變化規律相一致，表明翼尖渦的搖擺源自于翼尖渦內在的不穩定性特征。

3) 在不同的擾動波數作用下，模態P與模態S的演化機理不同。增加流向擾動波數，模態P切向波數逐漸增加；而模態S則是徑向波數逐漸增加。不同工況下，模態P的切向波數m=5～6，擾動流向波數分布在[2.75， 5]的區間內，對應的擾動流向波長為λ≈0.03 m，與翼尖渦0.01 m的渦核半徑可比，表明試驗中產生的同轉渦對所呈現的是一種短波不穩定性。

4) 在不同工況條件下，模態P所對應的不穩定放大率均要大于模態S，而且對攻角、雷諾數等來流條件的改變更為敏感。不穩定放大率最大模態的擾動范圍作用于上主渦的整個渦核區域，表明這種螺旋狀、大切向波數的擾動模態在翼尖渦流控中的潛在價值，也表明小翼通過增加渦系的個數，可以增強不穩定的發展，實現翼尖渦快速衰減的目標。