基于ARMA—GARCH模型的人民幣匯率波動性研究
李明軒 俞翰君

摘要:2015年新匯改制度的實施是繼2005年匯率制度改革之后的又一重大改革,人民幣匯率的波動受到了業界內外的高度關注,對人民幣匯率的波動性研究在經濟和金融等方面具有巨大的意義。本文選取了2015年6月1日到2020年6月30日的人民幣匯率每日中間價數據集作為對象,建立ARMA模型得到均值方程來消除序列的自相關性,結合GARCH模型、EGARCH模型、TGARCH模型和GARCH-M模型建立波動率方程對數據進行擬合,實證分析結果表明人民幣匯率具有集群性和杠桿效應等特征。最后給出控制和防范人民幣匯率波動的相關政策建議。
關鍵詞:人民幣匯率? GARCH模型? 集群性? 杠桿效應
一、引言
2005年7月21日,我國開始采用新的浮動匯率制度,這一制度的實施使得人民幣匯率的波動性得到進一步增強,波動的條件異方差性更為嚴重,對匯率序列建模提取方差方程顯得尤為重要。2015年8月11日,中國央行決定對人民幣兌美元匯率中間價報價機制進行調整,這一調整使得人民幣匯率與市場聯系更加緊密,可以更好地反映供求關系[1]。總而言之,新匯改后的匯率變化在經濟、金融、貿易等方面發揮著巨大的作用。
提到匯率往往第一時間想到的是匯率水平,從而忽視了波動性問題,近幾年匯改制度的實施使得匯率波動性問題在社會上引起了廣泛的關注,對于這一問題大多是基于GARCH類模型進行研究。蘇建平(2012)以1990-2010的宏觀數據作為研究的對象,使用VAR模型從計量經濟的角度分析人民幣匯率與外貿發展的相互關系,結果顯示通過了格蘭杰因果檢驗,人民幣匯率與我國外貿發展之間存在雙向關系[2]。胡昱琳(2016)建立了Copula—GARCH—t模型對波動進行實證研究,把人民幣對美元、歐元、日元、港元的收益率序列用于建模,發現人民幣受美元影響最大,并以此為基礎對機制的改革提出政策建議[3]。孫少巖、孫文軒(2019)以2016年10月10日到2018年3月16日美元兌人民幣匯率中間價為研究對象,針對加入SDR后的人民幣匯率波動規律進行研究,發現選擇一定滯后階數ARMA—GARCH模型可以很好地刻畫匯率的波動趨勢[4]。本文分別對數據建立ARMA模型擬合均值方程消除自相關性,建立GARCH族模型擬合波動率方程消除條件異方差性,對人民幣匯率的波動率特征進行刻畫,最終提出防范政策。
二、理論介紹
(一)ARMA模型介紹
ARMA模型又叫“自回歸滑動平均模型”,是研究平穩時間序列模型的常用手段,其表達式如下:
該模型能夠很好地分析時間序列數據的線性部分,但是對于數據的非線性部分的分析不夠理想[5],所以對于一些金融市場波動率的問題,不能單獨地使用ARMA模型來分析,需要進一步的引入GARCH模型進行研究。
(二)GARCH模型介紹
ARCH模型又叫“自回歸條件異方差模型”,該模型主要為了解決數據的條件異方差性,由Engle提出并應用于波動性的研究。但是方差方程的滯后項有時會比較大,使用ARCH模型無法得到理想的波動率方程,為此1986年Bollerslev提出了GARCH(p,q)模型來改進ARCH模型的缺陷。因為金融時間序列數據大多是存在波動集聚現象,呈現厚尾分布特征,故使用該模型可以有效地消除數據導致的過度峰值問題。GARCH(1,1)模型常被用作建模工具應用于實際問題中。GARCH模型的表達式為:
(三)EGARCH、TGARCH、GARCH-M模型介紹
查閱相關文獻發現,波動的非對稱性是金融類時間序列數據的常見特征,金融股票市場上,刺激股價上漲帶來的波動沒有刺激股價下跌帶來的波動大,因此當股票價格下跌時,波動率上升;當股票價格上升時,波動率下降,這種負沖擊效應被稱為杠桿效應。為了更好地研究這種效應[6],引入幾種特殊的GARCH模型。分別是EGARCH模型、TGARCH模型和GARCH-M模型,具體表達式為:
三、實證分析
(一)數據選取
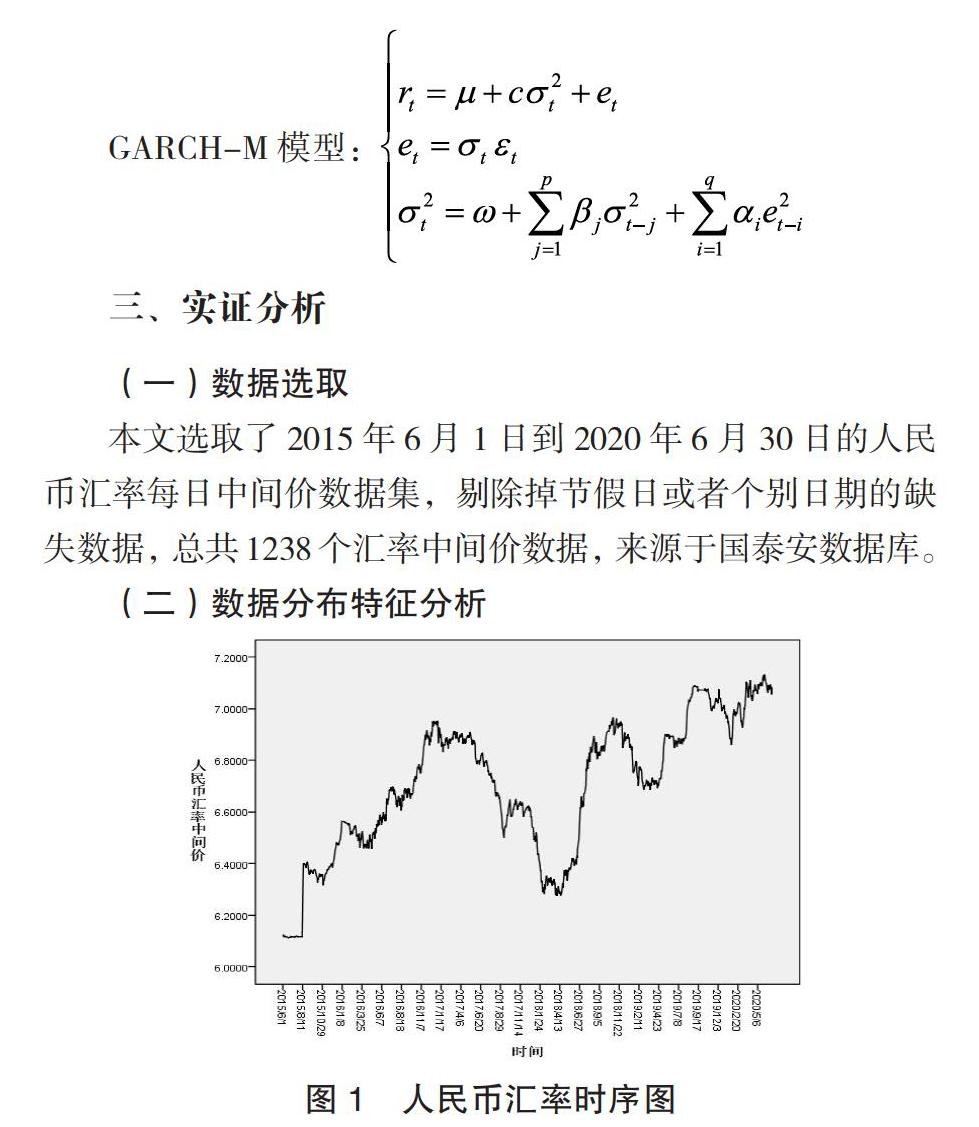
本文選取了2015年6月1日到2020年6月30日的人民幣匯率每日中間價數據集,剔除掉節假日或者個別日期的缺失數據,總共1238個匯率中間價數據,來源于國泰安數據庫。
(二)數據分布特征分析
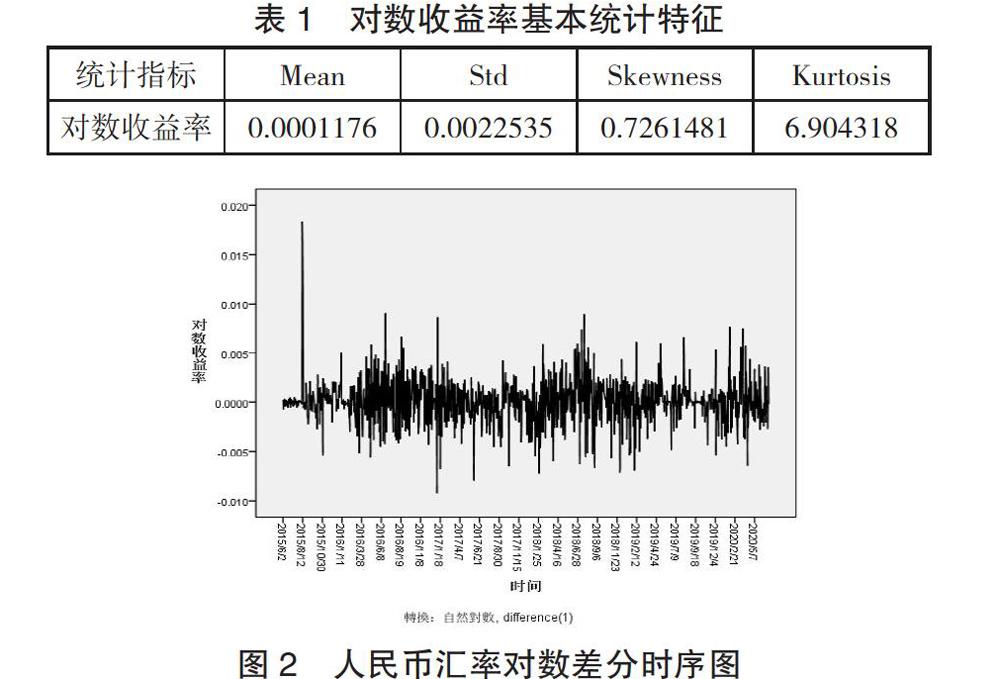
由圖1結合國際上發生的大事件可以得出2015年8月匯改之后人民幣匯率的振幅日益增大;2018年初,中美貿易摩擦問題加劇,中美雙方都對某些重點企業加征關稅,影響了中國很多企業的對外出口,這一狀況產生的負面情緒一直影響著匯率走勢。2019年,摩擦一波三折,更加難以控制,人民幣匯率起伏更大;2018年末到2019年4月,貿易戰開始呈現出緩和的勢頭,負面影響得到很好地控制,趨于穩定狀態,匯率出現了短暫的升值態勢。2020年1月21日新冠肺炎疫情大規模擴散之后,全國停產停業,人民幣匯率快速從6.86上升到了春節假期后的7.01附近,對經濟造成了一定的沖擊,之后人民幣匯率雖然有上升有下降,但是基本保持了一個穩定的走勢。圖1顯示該序列存在一定的增長趨勢,而且隨著序列值的增大,圍繞該值的波動情況并不穩定,因此可以通過計算它的對數差分序列消除以上趨勢,得到對數收益率序列,如圖2所示,處理公式如下:rt=ln(Pt)-ln(Pt-1)從表1可以看出該序列指標skew=0.7261481>0,kurt= 6.904318>3,呈現尖峰厚尾分布特征。另外從圖2看出序列的波動在某些時間段上比較低,而在其他時間段上又明顯比較高,展現了金融時間序列的波動集聚現象,可能存在條件異方差性。
(三)構建ARMA模型
1.單位根檢驗。平穩的時間序列是構建ARMA模型的前提條件,因此需要先檢驗數據是否滿足平穩性,使用R語言對對數收益率序列進行單位根檢驗,得到檢驗結果p-value=0.01,表明該序列通過了單位根檢驗,可以用于構建時間序列模型。
2.模型識別。根據對數收益率序列的ACF圖、PACF圖以及EACF圖,初步識別出AR(1)、MA(1)和ARMA(1,1)三個模型并進行參數估計。使用R語言輸出不同的參數估計結果,根據AIC或BIC信息準則,確定出相對最適合的模型,結果顯示AR(1)模型AIC值最小,選擇AR(1)模型最為合適,但是常數項系數不顯著,故將其剔除,得到最終的模型的表示式為:
3.模型檢驗。在建立ARMA模型得到均值方程之后,需要對該模型進行殘差檢驗,測試該模型的殘差是否為白噪聲序列。如果檢驗結果表明殘差不是白噪聲的分布,說明序列中還存在著未提取充分的相關信息,ARMA模型選擇的不合適,方程需要進一步更改。使用R語言軟件得到白噪聲測試結果見表2。
表2在自由度為5、11、17三種情況下對殘差序列進行了白噪聲的測試,以自由度為5為例,結果顯示X-squared統計量的值為4.9353,查卡方檢驗臨界值表得,自由度為5,顯著性水平為0.05時對應的臨界值為11.07。統計量的值小于臨界水平,p-value>0.05,故通過了白噪聲檢驗,均值方程已提取充分。
(四)構建ARMA—GARCH組合模型
1.ARCH效應檢驗。前文建立的AR(1)模型的殘差序列可能存在條件異方差性,需要ARCH效應檢驗來確定條件異方差性是否真的存在,只有存在ARCH效應的序列才可以建立GARCH模型。
McLeod—Li檢驗和LM檢驗是ARCH效應檢驗的兩種常用方法。本文以McLeod—Li檢驗為例,對AR(1)模型的殘差序列進行ARCH效應檢驗,檢驗結果如圖3:
從圖3可以看出所有p值點均在直線的下方,故拒絕原假設,有理由認為殘差序列存在ARCH效應,可以建立GARCH模型。
2.AR—GARCH模型。根據殘差序列平方和絕對值的樣本EACF圖的輸出結果,最終使用GARCH(1,1)模型來刻畫波動率的特征,前文已經估計了均值方程AR(1)模型,故本文利用AR(1)—GARCH(1,1)模型來擬合對數收益率序列,結果見表3。
由表3可知,所有參數系數均顯著,GARCH系數beta1= 0.6411,ARCH系數alph1=0.1446,beta1+alph1=0.7857<1,滿足GARCH過程平穩性的條件。擬合的AR—GARCH模型輸出結果顯示匯率過去的波動對未來的影響是衰減的。擬合效果理想,模型方程為:
從表4可以看出,Jarque-Bera Test統計量值很大,正態性檢驗不通過。對標準化殘差進行Ljung-Box Test,p值檢驗結果同樣可以說明均值方程的充分性。對標準化殘差的平方進行Ljung-Box Test或者LM Arch Test,檢驗p值>0.05,故波動性已提取充分,波動率方程是合適的。
研究過程中發現簡單的GARCH模型能得到合適的波動率方程,但是若想進一步探究人民幣匯率的波動是否存在著杠桿效應,必須使用更加貼合數據的GARCH族模型。
3.AR—EGARCH模型。對數據建立EGARCH模型時,以AR(1)作為均值模型,使用R語言軟件建立AR—EGARCH模型反復擬合比較,根據AIC、BIC信息準則,得到EGARCH(1,3)可以較好地擬合數據集,估計結果見表5。
四、結論與建議
本文通過分析建模結果得到了如下結論:第一,對數差分后的對數收益率序列是平穩序列,對其進行描述統計分析,由偏度和峰度的檢驗結果可知序列是尖峰厚尾分布。第二,對相關數據進行自相關檢驗,序列自相關圖顯示存在相關性,可以選用AR模型來消除線性依賴。第三,擬合的AR—GARCH模型輸出結果顯示匯率過去的波動對未來的影響是衰減的。第四,對AR—EGARCH模型的建立和分析得到方程中的杠桿效應系數小于零,人民幣匯率的波動存在杠桿效應,對利壞消息比利好消息的反應更加強烈。
基于人民幣匯率波動性的研究結果,提出相關政策建議:一是人民幣的杠桿效應表明,人民幣升值或貶值會引起匯率的較大波動。由于美元國際上的重要地位,預期人民幣匯率仍會貶值,為此央行需要制定合理的匯率波動空間。二是人民幣匯率作為金融時間序列數據,波動具有集群性,一定程度上增加了金融體系的系統性風險,因此政府應采取中性偏緊的政策,監管匯率波動情況,適時給出合理建議。
參考文獻:
[1]周曉波,陳璋,王繼源.基于混合人工神經網絡的人民幣匯率預測研究——兼與 ARMA、ARCH、GARCH 的比較[J].國際經貿探索,2019(9):35—49.
[2]黃金.基于GARCH類模型的人民幣匯率波動性研究[J].知識經濟,2011(17):46—47.
[3]胡昱琳.基于Copula—GARCH—t模型的人民幣匯率波動實證研究[J].商場現代化,2016(5):234—236.
[4]孫少巖,孫文軒.加入SDR后人民幣匯率波動規律研究——基于ARIMA—GARCH模型的實證分析[J].經濟問題,2019(2):42—47.
[5]Jonathan D.Cryer,Kung—Sik Chan著.時間序列分析及應用R語言(第2版).潘紅宇等譯.北京:機械工業出版社,2011:40—58.
[6]宮舒文.基于GARCH族模型的人民幣匯率波動性分析[J].統計與決策,2015(12):159—161.
作者單位:首都經濟貿易大學統計學院

