以弧度制為例談概念課的教學

過琨

數學的研究對象是現實世界的空間形式和數量關系，數學是關于模式與秩序的科學，數學概念就是反映這些數學對象的本質屬性和特征的思維形式，掌握概念，實質上就是要理解一類事物共同的本質屬性。為了掌握概念，可以利用學習者認知結構中原有的概念，以定義的方式直接向學習者揭示概念的本質屬性，這種使學習者獲得概念的方式叫概念同化。新概念和原有概念之間肯定是有聯系的，但是學生未必能找到這種聯系，如果在教學中不重視，那么學生在理解新概念的時候會產生許多問題，進而對建立在新的概念上的其他知識的理解和運用產生困難，所以概念課的教學必須要認真對待，要讓學生知道為什么給出這個概念、概念是怎么來的。下面以弧度制為例來談談概念課教學的一些體會。

弧度制本身是一節很普通的概念課，完成習題并不難，但弧度制的引入以及適應這種度量方式我覺得是最值得注意的部分。

一、學情分析

通過對高二、高三這些已學習過弧度制學生的了解發現，由于教材中直接給出了1弧度角的定義，教師在教學中偏重于弧度制的運用，引入不足，使大部分學生感覺這一節的教學很生硬，他們并不理解為什么要使用弧度制，感受不到弧度制對三角學習的必要性，部分學生甚至認為弧度制增加了學習的難度，在解題時還是換算成角度來運算更符合他們的習慣，這說明弧度制的教學尤其是概念的引入是不能簡單按課本那樣直接給出的。

二、弧度制的引入

概念教學大致經歷這樣幾個階段：概念的提出—形成—明確—鞏固。其中新概念的引入環節非常重要，要理清概念形成的脈絡。上一節講授了任意角，任意角的表示和運算仍是用角度制來表示的，所以我提出一個角度的運算題：39°40′29″+46°31′50″，學生很快就能給出答案86°12′19″，我詢問學生是如何計算的，學生概括出計算時運用十進制和六十進制，正因如此，角度制下的運算比較煩瑣且易錯，這時我就提出問題：能不能在角度的運算中避免使用六十進制，而是采用最熟悉的十進制呢？很顯然角度制是不能滿足這一要求的，那能不能換一種方式來度量角呢？這就為弧度制這種新的度量方式的引入提出了必要性。

概念是一類事物的共同的本質屬性，使符號代表一類事物而不是特殊事物，但是學生的認知能力決定了只能從特殊到一般。為了讓學生能夠理解弧度制的由來，我設計了一個分組探究的環節。

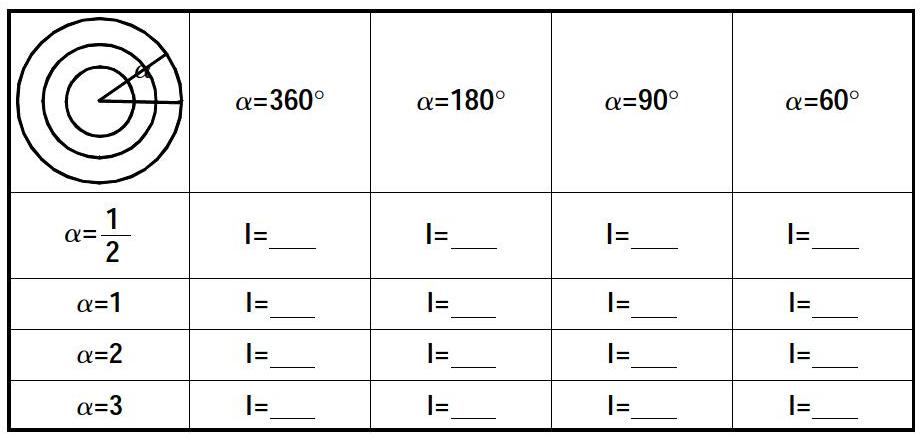
學生分成四個小組，按照給定的角度，選擇不同的半徑r，計算對應的弧長l，根據圖形的變化，猜想有什么不變的量。在小組探究的過程中，我發現學生在給定角和半徑的前提下計算弧長是不困難的，但是在尋找不變的量的過程中存在障礙，所以我適時提醒，在角不變的情況下，觀察弧長和半徑之間是不是存在什么關系。經過合作討論，有的小組從圖形上發現扇形之間具有三角形相似這樣類似的特點，將三角形相似的結論類比過來尋找不變的量，有的小組從弧長的計算公式中有了發現，我讓探究出成果的小組與大家交流，由于是學生從自己的認知能力出發探尋出的結論，大家理解起來不生硬，總結出當圓心角α的大小不變時， l/r的值不變，這時我就帶領大家發現l/r是一個由α的大小決定的十進制的數值，這就為利用十進制的數來表示角的大小提供了可能。

這種引入的方式避免了直接拋出新的概念，為學生的思維提供了一個緩沖、接收的時間，接下來對1弧度的定義的介紹就顯得沒那么突兀，而且學生在小組探究的過程能夠找到角度制與弧度制之間的關系，完成轉換。

三、弧度制的明確與鞏固

介紹了弧度制后，還要讓學生感受到它的好處，這樣才能避免學生學習了弧度制仍然化為角度制進行解題的尷尬。隨著弧度制下的弧長公式和扇形面積公式的給出，我讓學生對比兩種度量制下的公式，體會弧度制下的簡潔美;在后續的例題和練習中給出足夠的訓練，平時表示角度時盡量用弧度制來表示，削弱學生對角度制的依賴，建立起弧度制也是一個直接使用的數學概念，這些工作在后續的教學中是不可忽視，需要繼續進行的。

四、課后延伸

概念課的基礎性既是概念本身的基礎，又是建立其他概念和原理的基礎，所以不可以犯“重訓練輕引入”的錯誤，要重視概念學習過程中對學生數學思維能力的培養。在本節課的最后我讓學生觀察弧度制下扇形面積公式，思考：這個公式的形式你熟悉嗎？和哪個公式很相似？為什么？學有余力的學生可以接觸到微積分的一些概念，認識到弧度制的應用比角度制更為廣泛，更深層次地理解弧度制學習的必要性，大部分的學生在思考的過程中也能達到鍛煉思維能力的目的，這對學生數學素養的提高是很有幫助的。

參考文獻：

[1]曹才翰.中學數學教學概論[M].北京：北京師范大學出版社，1992.

[2]田萬海.數學教育學[M].杭州：浙江教育出版社，1992.

[3]朱水根，王延文，等.中學數學教學導論[M].北京：教育科學出版社，1948.

編輯 馮志強