在數學教學中如何培養學生的創新思維
汪 林
(安徽省合肥市肥西縣三河鎮中心學校 安徽 肥西 231200)
創新教育已成為新課改的一項重點內容。它所描述的內容往往是摸不著、看不見的,正因為這種抽象性給學生提供了巨大的想想空間,具有其他學科所不能替代的特殊作用。每個學生都有巨大的潛力和一定的創新能力,如何讓這些條件得以最大程都度的發揮呢?下面我就從以下幾個方面談談。
1.創設情境,激發學生的創新思
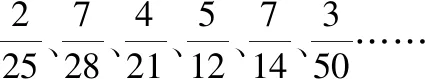
教師通過創設這樣的趣味情境不僅激發了學生的學習熱情,而且引導他們經歷了知識形成過,這樣的課堂才是有生命、有活力的課堂,學生在這樣的課堂中能不積極思考嗎?肯定能,因為他們是學習的主人翁!
2.鼓勵質疑,激發學生的創新欲望
創新思維來自質疑,思維永遠是從問題開始的。愛因斯坦曾經說過:“提出一個問題往往比解決一個問題更重要。”學習的過程就是不斷地提出問題、解決問題的過程。如“乘法分配律”的教學,在讓學生通過操作計算,初步得出規律后,再讓學生交流對“乘法分配律”的認識和看法。學生們提出:“幾個數的差同一個數相乘能不能用這個規律?” “只能是兩個數的和同一個數相乘能用這個規律嗎?三個、四個更多的數行嗎? “兩個數的和或差除以一個數,能用這個規律嗎?”...在老師的鼓勵和引導下,學生的問題一個接一個,敢于求新,言他人所未能言,問他人所未敢問的。
在課堂教學中,教師要創造寬松的教學環境,讓學生敢于發表自己的想法、勇于質疑、敢于創新,養成認真勤奮、獨立思考、合作交流的好習慣。
3.訓練側向思維,培養學生的創新思維
“側向思維法”是對某一問題不從正面去研究它,而是從側面入手進行分析,從而解決問題的一種思維方法。教師要善于挖掘資源以培養學生的側向思維。如有道題在公路的兩旁栽路燈,每隔10米栽一盞燈,現在共栽了42盞燈,請問這條路有多長?有的學生是這樣做的:“42÷2x10。”并解釋:42÷2是一邊載的樹,然后用除得的結果乘10就是這條公路的長度。我不作出任何評價,又出了一道題:如果把一根木料鋸成3段要用9分鐘,那么平均每次用幾分鐘?同學們很快就算出是4.5分鐘(因為3段只要鋸2次),那么請同學們再想想路燈這道題。有的在認真地算,有的在畫線段圖,有的在靜思......我巡視,并適時指導。良久,有個學生興奮地說:哦老師我明白了:“鋸木頭的次數總比段數少1,根據這個方法推,那么載路燈的燈數就相當于載數的棵數,如果把兩盞燈之間的距離作為一段,那么載路燈的段數就相當于鋸木頭的次數,也就是路燈與路燈之間的段數總比燈數少1,因此這道題應這樣做:(42÷2-1)× 10”我為學生的頓悟而感到高興。
側向思維法在解決問題時往往能收到意想不到的效果。因此教師在平時的教學中也要注重訓練。
4.開拓解題思路,培養學生的創新思維

新課標指出:數學和社會進步息息相關,更重的是它在培養人思維能力和創新能力方面具有不可替代的作用。只要教師用心挖掘,善于調動、培養,不僅能在課堂上培養學生的創新思維,提升學習效率,更能讓學生在日常學習、生活中養成創斯思維與習慣,成為社會主義現代化建設的合格接班人。

